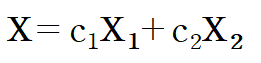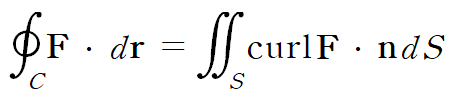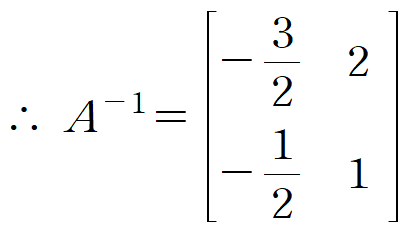SUBORATORY

#공업수학 ​ 푸리에 변환과 푸리에 역변환은 다음과 같습니다. ​ ​ 1. 푸리에 변환 ​ 푸리에 변환은 다음과 같이 정의됩니다. ​ ​ ​ 푸리에 변환의 경우 적분구간이 (-∞,∞) 이고 코사인, 사인 변환의 경우 (0,∞)라는 것에 주의합니다. ​ 푸리에 역변환에 있는 1/2π 항을 루트로 나눠서 푸리에 변환과 역변환에 각각 나누어 정의하기도 합니다(크레이지 공업수학) ​ ​ 2. 도함수 공식 편미분 방정식을 푸는 데 라플라스 변환을 사용하는 것처럼 푸리에 변환을 사용할 수도 있습니다. ​ *참고* https://blog.naver.com/subprofessor/222234339432 [공업수학] *편미분 방정식 예제 : 라플라스 변환* #공업수학 #라플라스변환 #편미분방정식 지난 시간에 이어 편미분..

간단한 변수분리형 1계 상미분 방정식을 풀어보자. 1.2는 방향장(direction field)에 관한 내용인데 깊게 들어가지 않고는 딱히 알 필요성이 적기 때문에 건너뛴다. 방향장이 뭔지 알고 싶은 사람은 아래 링크로 ​ https://blog.naver.com/NBlogTop.naver?blogId=roty22&Redirect=Dlog&Qs=/dydrogud22/220108163230 수학-방향장과 오일러 방법 지금까지 간단한 일계 미분방정식의 해를 구해 보았다. 해가 알려진 특별한 미분방... blog.naver.com ​ 1. 변수분리형 상미분 방정식의 형태 이번 시간에 다루는 변수분리형 미분방정식은 1계 미분방정식이다. 영어로는 separable ODE 혹은 separation of variab..

이번 시간에는 미분방정식을 분류하는 방법에 대해 알아보자. 마치 판사가 법정에서 이런 항목에 대해서 이러이러한 죄를 적용한다고 선언하는 것처럼, 유난히 격해지는 NBA플레이오프 시즌에 어떤 경우는 오펜스파울이고 어떤 경우는 디펜스파울인지 정하는 Rule이 있는 것처럼, 우리도 미분방정식을 잘 다루기 위해서는 그것들을 분류하는 Rule이 있어야 한다. 미분방정식을 푼다는것은 주어진 등식을 만족하는 y를 y=f(x)꼴의 함수로 정리하는 것을 의미한다.(상미분 방정식의 경우 한정) 그리고 우리가 분류하는 이유는 각 분류에 따라서 적용할 수 있는 쉬운 Solution이 다르기 때문이다. 간단하다. 몇 번 보면 익숙해지니 겁먹지 말도록! 아직 시작도 안했으니.. ;) ​ 1. 상미분 / 편미분 (ODE / PDE..

#2023학년도 수능 ​ ​ 2022년 11월 17일 (목)에 시행된 2023학년도 수능 수학 미적분 29번 손글씨 풀이입니다. ​ 사용된 개념으로는 지수함수 + 극한의 존재성 + 역함수의 적분 입니다. 조건을 해석하기 어려운 문제는 아니었습니다. ​

#공업수학 ​ Systems of Linear Differential Equations 연립 선형 미분 방정식 예제입니다. 라플라스 변환을 사용하지 않으며 행렬과 고윳값으로 해결합니다. ​ 1. Homogeneous Linear Systems 다음과 같은 형태의 미분방정식을 연립 제차 선형 방정식이라 부릅니다. A, X는 행렬입니다. 예시는 아래와 같습니다. 위 연립 미분방정식을 행렬 형태로 표시합니다. 1. Method ​ (i) get matrix A from Differential Equation X' = Ax (ii) find eigenvalue λ and eigenvector K from Characteristic Equation det(A-λI) =0 (iii) obtain general so..

#공업수학 ​ 스토크스 정리는 폐곡선에 대한 선적분을 보다 간단한면적분(Surface Integral)로 계산할 수 있도록 해주는 유용한 정리입니다. ​ ​ 1. Stokes' Theorem ​ ​ ​ "S를 부분적으로(piecewise) 매끄러운 닫힌 곡선 C로 둘러싸인 부분적으로(piecewise) 매끄러운 곡면이라 하자. 벡터함수 함수 F(x,y,z)의 x, y, z 편도함수가 곡면 S를 포함하는 공간에서 모두 연속일 때 다음 식이 성립한다." ​ 부분적으로 매끄럽다는 것은 구간으로 나누었을 때 각 구간에서 모든 점들이 미분가능하다는 것을 말합니다. 이때 폐곡선 C는 반시계방향, n은 곡면 S의 단위법선벡터입니다. T는 단위접선벡터인데 가운데 식은 본 게시글에서 다루지 않습니다. ​ ​ curl F..

​ 2022년 6월 9일 평가원 시행 문항 ​ ​ 손글씨 해설 ​ ​ ​ ​ 이차곡선의 성질에 대한 문제였으며 마지막 Q의 좌표는 포물선 C2 식을 구해서 C1과 연립해 구해도 됩니다. 이 경우 P의 좌표를 이용해 근과 계수의 관계로 Q의 좌표를 얻을 수도 있습니다.

#선형대수학​ 1. Introduction 최소제곱법은 주어진 데이터와의 오차를 최소화하는 직선을 구하는 방법입니다.​ ​​ 위 그림은 주어진 5개의 데이터에 대해 두 개의 점을 지나며 오차를 줄이는 적당한 직선(linear function)을 그린 것입니다.​ 그러나 몇 개의 점을 지난다고 해서 오차를 완벽히 줄일 수 있는 것은 아닙니다.​ ​​​2. Sum of the square errors​ ​    위 그림은 주어진 데이터(xi, yi)에 대해 그린 직선 y = f(x) 과의 오차 ei를 시각적으로 표현하였습니다. ei 는 yi 에서 선형함수의 함숫값 f(xi) 을 뺀 것의 절댓값으로 정의됩니다.​​ y = f(x)가 y = ax + b 형태로 표현된다고 합시다.​ 이때 error(distanc..

#선형대수학 ​ ​ 고윳값과 고유벡터에 대한 내용은 아래 글 참조 바랍니다 https://subprofessor.tistory.com/58 [선형대수학] 고윳값, 고유벡터, 고유공간 (Eigenvalue, Eigenvector, Eigenspace) #선형대수학 ​ ​ 1. 고윳값과 고유벡터의 정의 n x n 행렬 A에 대해 위 등식을 만족하는 λ(lambda)와 x를 각각 고윳값(Eigenvector), 고유벡터(Eigenvector)라 합니다 ​ ​ 위와 같은 2 x 2 행렬을 생각해봅. subprofessor.tistory.com https://subprofessor.tistory.com/57 [선형대수학] 특성방정식, 고윳값과 고유벡터 구하기 #선형대수학 ​ 1. 특성방정식 (Characteris..

#미분적분학 ​ 1. Definition 다변수함수에서 x, y, z 에 대한 편미분도 가능하지만 임의의 벡터를 기준으로 도함수를 구할 수도 있습니다. 이것을 방향도함수(Directional Derivative)라 부르며 다음과 같이 정의됩니다. ​ ​ ​ ​ 점 P에서 f(x,y,z)의 벡터 b 방향으로의 방향도함수 Dbf 또는 df/ds 는 식 (2)와 같이 정의됩니다. 이때 Q는 P를 지나며 b를 방향벡터로 갖는 직선 L에서 P로 다가가는 움직이는 점이고 s는 P와 Q사이의 거리입니다. ​ ​ ​ 방향도함수의 계산은 gradient 를 이용합니다. 이때 b는 단위벡터입니다. ​ ​ 임의의 크기를 가지는 벡터에 대한 방향도함수의 계산은 벡터의 크기로 나누어주는 것으로 정의됩니다. ​ ​ ​ ​ ​ 다..