Systems of Linear Differential Equations
연립 선형 미분 방정식 예제입니다.
라플라스 변환을 사용하지 않으며 행렬과 고윳값으로 해결합니다.
1. Homogeneous Linear Systems
다음과 같은 형태의 미분방정식을 연립 제차 선형 방정식이라 부릅니다.
A, X는 행렬입니다.

예시는 아래와 같습니다.

위 연립 미분방정식을 행렬 형태로 표시합니다.


1. Method
(i) get matrix A from Differential Equation X' = Ax
(ii) find eigenvalue λ and eigenvector K from Characteristic Equation det(A-λI) =0
(iii) obtain general solution


예외가 몇 가지 있습니다.
(a) multiple eigenvalue
- 중복되는 고윳값의 수만큼 서로 다른 고유벡터가 있을 경우 상관 없습니다.

- 중복되는 고윳값의 수보다 고유벡터의 수가 적을 경우 아래와 같은 방법을 사용합니다.
중복도가 3인 고윳값에 대응하는 고유벡터가 1개인 예시입니다.


(b) complex eigenvalue
- complex eigenvalue λ = α + βi 의 켤레복소수 또한 고윳값입니다.
- complex eigenvalue λ = α + βi 에 대응하는 고유벡터 K 의 켤레복소벡터는 켤레복소수 고윳값에 대응하는 고유벡터입니다.
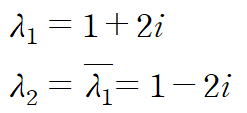
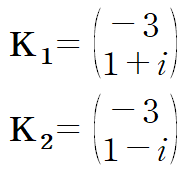
- real solution of complex eigenvalue

이때 B1, B2 는 각각 K1의 실수부 벡터, 허수부 벡터입니다.

2. Example
(예제 1) find the general solution of the given system

(i) get matrix A from Differential Equation X' = Ax


(ii) find eigenvalue λ and eigenvector K from Characteristic Equation det(A-λI) =0

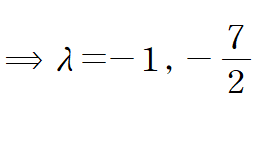

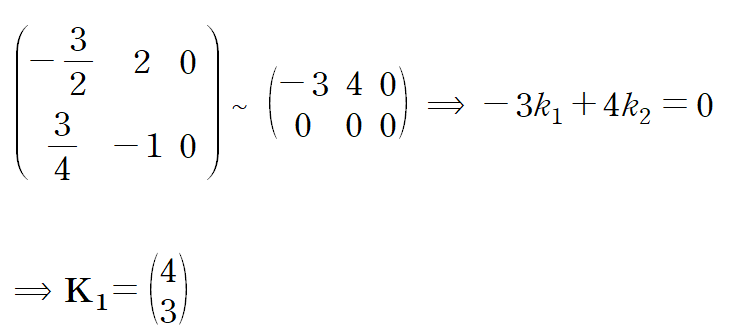
같은 방식으로 K2를 구합니다

(iii) obtain general solutions
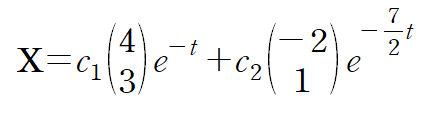
(예제 2) find the general solution of the given system

(i) get matrix A from Differential Equation X' = Ax

간단히 계수만 따오면 됩니다.
(ii) find eigenvalue λ and eigenvector K from Characteristic Equation det(A-λI) =0


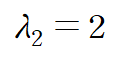
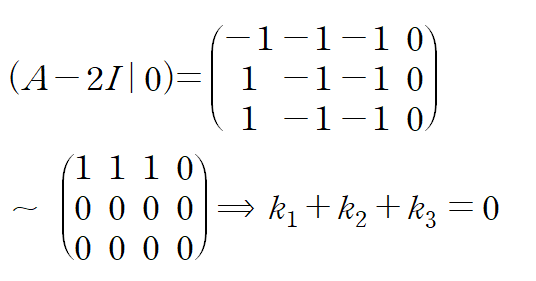


고윳값 2에 해당하는 고유벡터는 중복도의 수와 동일한 두 개입니다.

(iii) obtain general solution
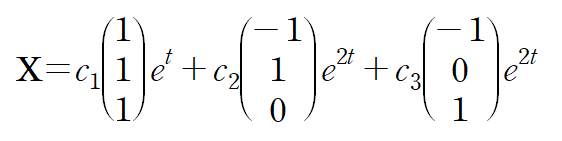
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식) (0) | 2022.12.27 |
|---|---|
| [공업수학] 1.1 미분방정식의 분류 (0) | 2022.12.26 |
| [공업수학] 스토크스 정리(Stokes' Theorem) 예제 (0) | 2022.12.13 |
| [공업수학] *편미분 방정식 예제 : 라플라스 변환* (0) | 2022.06.17 |
| [공업수학] 1계 상미분방정식 총정리 (2) : 동차방정식(제차방정식), u = ax+by+c 꼴 치환 (0) | 2022.03.21 |