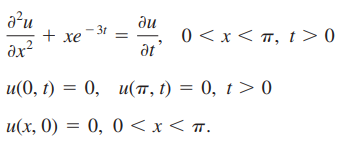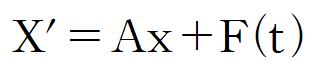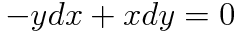SUBORATORY

#공업수학 ​ 제차 편미분 방정식의 소개와 푸리에 변환을 활용한 풀이는 아래 게시글 참조 바랍니다 https://subprofessor.tistory.com/151 [공업수학] 편미분 방정식 (1) : 변수분리부터 푸리에 변환까지 #공업수학 ​ ​ ​ 푸리에 코사인, 사인 급수에 대한 내용은 아래 게시글 참조 https://blog.naver.com/subprofessor/222311262488 [공업수학] 푸리에 사인 급수, 푸리에 코사인 급수 #공업수학 #푸리에급수 오 subprofessor.tistory.com ​ ​ ​ 1. Types of Nonhomogeneous PDEs ​ 비제차 방정식은 독립변수로 이루어진 항 또는 종속변수 항이 존재하는 미분 방정식입니다. 아래 편미분 방정식을 예시로 들..

지금까지는 1계 미분방정식 즉 y'가 들어간 미분방정식의 해를 구해보았다면, 이제 y''가 들어간 2계 미분방정식을 다루어봅시다. 2계 미분방정식의 활용도는 정말 높아서(F=ma라던지) 공대생이라면 필수적으로 알아야 하는 파트입니다. 그 기반이 되는 "2.1 Homogeneous Linear ODEs of Second Order"는 양 자체가 거대하기도 하고 나중에도 쓰이는 Basic Material이 많기 때문에 세 파트로 나눠서 포스팅 합니다. ​ ​ (i) 2계 선형방정식의 형태 2계 선형 상미분방정식(Linear ODEs of Second Order)의 형태는 다음과 같습니다. 기본적인 형태는 1계 선형방정식과 크게 다름이 없죠? ​ 이런 애들을 2계 선형 상미분 방정식이라고 분류합니다. 2.1에..

Homogeneous Linear ODEs of Second Order의 Fundamental Theorem인 중첩원리를 증명해 보겠습니다. ​ ​ ​ 아래 2계 제차 선형 상미분 방정식 (1)을 봅시다. ​ p=p(x) / q=q(x)는 p와 q가 오직 x의 함수라는 것을 의미합니다. ​ ​ ​ ​ 이제 이 식들을 처음 방정식에 대입해서 정리합니다. ​ ​ ​ ​ Any Qustions, Any Comments are WELCOME :) 오타나 오류 지적 감사히 받습니다

이번시간에는 베르누이 방정식에 대해서 알아봅시다. 이 베르누이 방정식이라는 특별한 형태의 미분방정식을 아는 것도 중요하지만 "치환"을 해서 선형방정식을 유도하는 과정을 익히는 것이 더 중요합니다. ​ (i) 베르누이 방정식 위 형태의 방정식을 우리는 1계 선형 상미분 방정식 이라고 분류했었고, 어떻게 푸는지도 1.5-1에서 공부했습니다. ​ 그렇다면 우변이 위와 같은 형태로 되어있을 때는 어떻게 해야 할까요? 우변의 a가 0 또는 1인 경우에는 1.5-1에서 배운 1계 선형 상미분 방정식 푸는 방법으로 풀면 되는데, 그렇지 않은 경우에는 비선형방정식(nonliear equation) 이 됩니다. 이런 방정식은 어떻게 풀 수 있을까요? ​ 결론부터 말하자면 이놈을 이용합니다. ​ (a)식의 양변을 x에 대..

#공업수학 ​ Systems of Linear Differential Equations 연립 선형 미분 방정식 예제입니다. ​ ​ 연립 제차 방정식에 관한 이해가 선행됩니다. https://subprofessor.tistory.com/129 [공업수학] 연립미분방정식 예제 : 제차 방정식 (Homogeneous Equation) #공업수학 ​ Systems of Linear Differential Equations 연립 선형 미분 방정식 예제입니다. 라플라스 변환을 사용하지 않으며 행렬과 고윳값으로 해결합니다. ​ 1. Homogeneous Linear Systems 다음과 같은 형태의 subprofessor.tistory.com 또한 비제차 방정식을 푸는 데 필요한 매개변수법과 https://blog...

조금은 충격적이었던 완전미분방정식이었습니다. 그에 비하면 오늘 배우는 선형 상미분방정식은 조금 낫습니다. 1.1 미분방정식 분류에서 선형/비선형에 따른 분류를 다들 기억하고 있지요? 가물가물하다면 위 파란 글씨 클릭하셔서 복습하시고 본 챕터 시작하시길 추천합니다. 앞서 배운 선형이라는 개념을 토대로 1.5 선형 상미분방정식을 배워봅시다. ​ (i) Linear ODEs 1계 상미분 방정식이 다음과 같은 형태일 때, 선형성을 갖습니다. 또는 ​ 둘 다 같은 의미의 식이지만, 이번 시간에서는 둘 중 (a)-1형태의 상미분방정식을 주로 다룹니다. r(x)를 우변에 홀로 두고 계산하는 것이 편하기 때문입니다. (ii) Homogeneous Linear ODE (제차 선형 방정식) ​ 위 식에서 r(x)=0일때,..

이번 챕터는 완전미분방정식이 아닌 애들을 완전미분방정식으로 만들어주는 적분인자에 대해서 알아봅시다. Basic Concept는 그러한 함수 F가 있다고 가정하고 완전성 검사를 통해서 F를 구하는 느낌입니다. 그 뒤는 완전미분방정식의 해를 구하는 방법과 동일합니다. ​ (i) Basic Concept Basic Concept는 이렇습니다. 완전미분방정식이 아닌 것에 완전성을 부여한다. 미지의 함수 F로 말입니다. 위와 같은 미분방정식을 예로 들어봅시다. 완전성 검사를 시행했을 때, nonexactness임을 알 수 있는데요, 이 식의 양변에 1/x^2 즉 를 곱해줍시다. 그러면 다음과 같은 식이 되는데요 이 식은 완전성을 가짐을 직접 해봄으로써 알 수 있습니다.(꼭 해보세요!) ​ ​ 느낌오시나요? non..

지난 시간에는 완전미분방정식이 무엇인지, 어떻게 판별하는지, 어떻게 푸는지에 대해서 알아보았습니다. 풀이과정이 다소 길고 복잡하기 때문에 예제 파트를 따로 나누었습니다. 이번 포스팅에서는 네 개의 미분방정식 예제를 소개하는데, 이를 통해 완전미분방정식에 대한 감이 잡히길 바랍니다 ​ ​ (예제 1) 다음 미분방정식의 완전성을 검사하여라 ​ dx앞에 있는 놈들을 y에 대해 편미분해주고, dy앞에 있는 놈들을 x에 대해 편미분해줍니다. ​ 음! 뭔가 둘이 안맞네 하죠? 맞아요 완전미분방정식이 아닙니다. 이런 간단한 문제가 시험에 나올 일은 없지만 만약 나온다면 저는 이렇게 답안을 작성할 것 같네요 ​ ​ 해당 미분방정식에 대해 완전성 검사를 시행한 결과 이므로 완전미분방정식이 아닙니다. ​ ​ ​ ​ (예제..

슬슬 뜨악할 수준이 슬금슬금 보인다. 오늘 배울 완전미분방정식의 기반을 이루는 개념은 편미분과 관련이 있다. 편미분 관련 지식은 다음 블로그에서 참조하면 된다. 본 블로그와는 다르게 매우 친절히 소개하고있다. https://blog.naver.com/mrhyde/60061507248 전미분, 편미분 편미분과 전미분 ∂ 는 편(偏)미분 기호입니다...여러 변수 중에서 1개의 변수에 대해서만 미... blog.naver.com 솔직히 가독성은 조금 떨어지는데(..) 이번 1.4-1을 위해 알고있어야 하는 개념을 모두 담고있는 좋은 글이니 알고있던 사람도 한번 들어가볼것. 1. Basic Concept x, y에 관한 다변수함수 z를 위와 같이 정의할 때, 미분소 dz는 아래와 같이 정의된다. 이것이 알아야 ..

#공업수학 ​ ​ ​ 푸리에 코사인, 사인 급수에 대한 내용은 아래 게시글 참조 https://blog.naver.com/subprofessor/222311262488 [공업수학] 푸리에 사인 급수, 푸리에 코사인 급수 #공업수학 #푸리에급수 오늘은 푸리에 급수 중 주어진 주기함수가 기함수 또는 우함수인 경우 분류되는 푸... blog.naver.com ​ 푸리에 변환에 대한 내용은 아래 게시글 참조 https://blog.naver.com/subprofessor/222962220759 [공업수학] 푸리에 변환(Fourier Transform) #공업수학 푸리에 변환과 푸리에 역변환은 다음과 같습니다. 1. 푸리에 변환 푸리에 변환은 다음과 같이 정... blog.naver.com ​ 1. Separab..