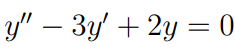SUBORATORY

#라플라스변환#공업수학  라플라스변환으로 미분방정식 문제 세 개를 풀어봅시다.예제 1 : 기본적인 상수계수 2계 미분방정식예제 2 : 단위계단함수예제 3 : 디랙 델타​​  ​(예제 1) 미분방정식의 해를 구하여라​​라플라스 변환으로 미분방정식을 풀려면 도함수 공식을 알고 있어야 합니다.https://blog.naver.com/subprofessor/222200501838 [공업수학] 6.2-1 라플라스 변환 : 도함수 공식#공업수학 지난 시간에 이어 라플라스 변환의 근본을 이루는 도함수 공식을 알아봅시다 미분 공식(도함수 ...blog.naver.com  ​​> 도함수 공식​​(1) 주어진 미분방정식의 양변에 라플라스 변환을 취합니다.도함수 공식을 적용하고Y에 대해 정리합니다. ​(2) 부분분수 분해부..

#선형대수학​단위행렬 I 에 대해서는 행렬을 인수분해처럼 다뤄도 괜찮다.​어차피 행렬곱 과정에서 소거가 되기 때문인데요, 예제를 보겠습니다.​​​​(예제 1) 행렬 M에 대하여 M^3를 구하여라. 이때 행렬 M의 세제곱을 직접적으로 계산해서는 안된다. ​​​아래와 같이 행렬 M을 인수분해할 수 있습니다.​이렇게 인수분해할 수 있는 것은 단위행렬이기 때문입니다.​분해된 행렬을 계산하는 것은 비교적 간단합니다. ​따라서 M의 세제곱은 아래와 같이 계산됩니다. ​​​​​​​​이보다 더 깔끔한 상황이 있습니다.​​​​​(예제 2) 주어진 행렬을 적절한 두 행렬의 합으로 표현하여 역행렬을 구하여라Hint : 행렬의 거듭제곱 ​​ ​  ​​​먼저 A를 I+B로 분해할 수 있습니다.​이때, I+B^3은 다음과 같이 ..

​이번 글에서는 멱급수와 멱급수의 수렴반경을 알아봅시다. 목차1. 서론2. 멱급수를 간단한 함수로 표현하기3. 멱급수의 수렴  1. 서론멱급수(power series)는 다음과 같이 다항함수들의 합으로 표현된 급수를 말합니다.​Cn은 x^n의 계수입니다.​멱급수는 x의 값에 따라 수렴할수도 있고, 발산할 수도 있습니다. ​급수의 수렴/발산을 조사하는 여러 가지 test가 있습니다.https://blog.naver.com/subprofessor/222100880217 [미분적분학] 교대급수 판정법#미분적분학 오늘은 무한급수의 합이 수렴하는지, 발산하는지 알 수 있는 판정법(Test) 중 교대급수 판정...blog.naver.com  https://blog.naver.com/subprofessor/22210..

#선형대수학 https://subprofessor.tistory.com/198   [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지#선형대수학 #공업수학 ​ ​ Contents - Eigenvalue(고윳값 또는 고유치) & Eigenvector - Diagonalization - Spectral Decomposition ​ ​ ​ ​ 1. Eigenvalue & Eigenvector 고윳값(또는 고유치)과 고유벡터는 정방행렬 A(squasubprofessor.tistory.com   행렬을 다른 행렬들로 분해(Decomposition)하는 방법은 다양합니다.​LU분해QR분해대각화​등등..​특이값 분해(SVD)는 대각화가 nxn 정방행렬만 가능한 것과 달리, 일반적인 mxn 행렬에 대해서 수..

#선형대수학  선형방정식에 대해 두 글에 걸쳐서 알아봤는데 이번에는 직접 선형방정식을 풀어보는 시간을 가져봅시다. 예제와 함께 풀이가 나와있긴 하지만 직접 풀고 풀이를 확인하는 것을 추천합니다​​​(예제 1) 첨가행렬로 표현된 아래 선형방정식계의 해를 구해라​​​​​ 먼저 첨가행렬을 Echelon form으로 바꾸어야 합니다​ 두 번째 행 중 가장 왼쪽에 위치한 항이 0이 되도록(정확히는 첫 번째 행에 위치한 leading entry 아래가 0이 되도록) 첫 번째 행에 -3을 곱한 것과 두 번째 행을 더하는 ERO(기초 행 연산, Elementary Row Operation)을 수행합시다Replacement​​​​​ 해를 구하기 위해서는 행렬을 Echelon form 다음 Reduced echelon f..

한양대 2023학년도 자연계열 수학 기출 ​ ​ 공업수학 과목에 속한 미분방정식 문제가 나왔습니다. ​ 1. Main Concept 미분방정식 중에서도 1계 상미분 방정식 단원의 "완전미분방정식"(Exact ODE)이 출제되었습니다. ​ 완전미분방정식을 푸는 방법은 다음과 같습니다. ​ ​(1) 완전성 검사 : M을 y에 대해 편미분한 것과 N을 x에 대해 편미분한 것을 비교한다. (2) u = int(M) dx +k(y) 로 설정. 또는 u = int(N)dy + k(x) 로 설정. (3) u의 편도함수가 N임을 (M임을) 이용해 k(y) 또는 k(x)를 결정한다. (4) u = C꼴의 해를 정리한다. ​ 만약 (1) 완전성 검사(test exactness)를 수행했는데 양변이 다르다면 적분인자를 구해..

한양대 2023학년도 자연계열 수학 기출 ​ ​ 선형대수학 과목에 속한 행렬식 문제가 나왔습니다. ​ 1. Main Concept 행렬식의 성질을 이용해 크기가 큰 행렬의 행렬식을 계산하는 문제가 출제되었습니다. ​ 연립방정식의 해를 구할 때 처음 등장한 기초 행연산(기본행연산; Elementary Row Operation)이죠 기존의 행렬을 A, 기초행연산을 수행한 행렬을 B라고 하면 다음 관계가 성립합니다 ​ (1) 은 두 행의 위치를 바꾸는 interchange (2) 은 한 행에 상수를 곱해 다른 행에 더하는 replacement (3) 은 한 행에 상수배를 곱하는 scaling ​ ​ ​ ​ ​ 2. Problem 이 문제는 거기에 더해 "삼각행렬의 행렬식"이라는 개념이 추가되었습니다. ​ 왼쪽..

#공업수학 #미적분학 오늘은 푸리에 급수전개를 구하는 몇 가지 예제를 풀어봅시다 목차 0. Intro 1. Definitions 2. Examples 3. Summary ​ https://blog.naver.com/subprofessor/222150692985 [미분적분학] 푸리에 급수 (Fourier Series) #미분적분학 사실 Erwin O. Kreyszig의 공업수학에 나오는 내용이지만 너무 AWESOME한 개념이기... blog.naver.com 푸리에 급수란, 주기함수를 삼각함수들의 합으로 나타낸 것을 말합니다. 테일러 급수와 같이 함수 f(x)를 기본적인 함수들로 쪼개어 나타내는 것인데, 푸리에 급수는 "주기 함수"를 대상으로 한다는 특징이 있습니다. https://blog.naver.co..

#선형대수학 > 미리보기 ​ ​ ​ ​ 1. Approximation of Eigenvalues 행렬의 거듭제곱(power method)을 계산하여 고유값의 근사치를 구할 수 있습니다. ​ Xm이 행렬의 거듭제곱과 어떤 벡터 X0의 곱으로 정의될 때 ​ 고유값은 다음과 같이 근사할 수 있습니다. 위 식의 우변을 Rayleigh quotient라 부릅니다. ​ 예시로 아래와 같은 2x2 행렬을 봅시다. ​ 먼저, 임의의 X0를 설정합니다. 통상적인 고유값 계산 과정은 행렬식을 이용하는 것이지만 우리는 다른 방법으로 고유값의 근사치를 구할 것입니다. ​ 연산이 많으니 가급적 간단한 X0를 사용하는 것이 좋겠죠? ​ ​ 다음으로 행렬의 거듭제곱을 사용해 적당히 큰 Xm을 얻습니다. ​ ​ 이를 반복해 X7까지..

#선형대수학 2차원 평면에서 반시계방향으로 θ만큼 회전한 회전행렬은 다음과 같이 표현된다 ​ ​ 열벡터 형태로 표시된 [x,y]를 이 행렬에 곱하면 반시계방향으로 θ만큼 회전이 된다. ​ 여기서 [x,y]가 의미하는 것은 점이 될 수도 있고, 도형이 될 수도 있다. ​ ​ ​ ​ 이것을 사용해 이차곡선을 회전시킬 수도 있다. ​ ​ 위 타원을 반시계방향으로 45도 회전한 도형의 방정식을 구해보자 ​ 먼저 회전행렬을 정의하고 ​ 그 다음 회전 변환 식을 이용해 ​ x', y' 에 대한 식을 얻는다. ​ 우리가 가지고 있는 것은 x, y에 대한 관계식(타원의 방정식)이므로 ​ x와 y에 대해 식을 정리해서 넣어주자 ​ ​ 타원에 방정식에 정리한 x, y를 넣어주고 정리하면 ​ 아래와 같은 식을 얻는다. ​ ..