
1. Stokes' Theorem

"S를 부분적으로(piecewise) 매끄러운 닫힌 곡선 C로 둘러싸인 부분적으로(piecewise) 매끄러운 곡면이라 하자. 벡터함수 함수 F(x,y,z)의 x, y, z 편도함수가 곡면 S를 포함하는 공간에서 모두 연속일 때 다음 식이 성립한다."

부분적으로 매끄럽다는 것은 구간으로 나누었을 때 각 구간에서 모든 점들이 미분가능하다는 것을 말합니다.
이때 폐곡선 C는 반시계방향, n은 곡면 S의 단위법선벡터입니다. T는 단위접선벡터인데 가운데 식은 본 게시글에서 다루지 않습니다.

curl F은 ▽ 와 F의 외적입니다.

S의 단위법선벡터 n은 다음과 같은 과정으로 구합니다.

곡면 S가 z의 함수로 표현될 때 법선벡터는 다음과 같습니다.(N = ▽(g(x,y)-z) )

x, y 일때 N입니다. 각각 x = g(y,z), y = g(x,z) 로 곡면 S가 표현되는 상황입니다.

이것을 N의 크기로 나눈 것이 단위법선벡터인데
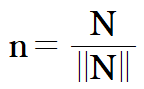
굳이 이렇게 계산하지는 않습니다.
일반적인 경우 ndS = NdA 이기 때문에 굳이 분모에 근호가 포함된 식을 구할 필요가 없습니다.(어차피 소거됨)
dS는 곡면의 미소면적이고 dA는 곡면 S를 xy평면 (z = g(x,y)의 경우) 으로 사영(projection)시킨 영역 R의 미소면적 입니다.


단순한 중적분처럼 계산할 수 있다는 장점 때문에 저는 아래 식을 더 선호합니다.

2. Example
(예제 1) S가 아래 그림과 같을 때 이를 둘러싼 곡선 C에 대해 F의 선적분 을 계산하여라
벡터장 F = [xy, yz, xz] 이다.

곡선이 네 개의 구간으로 나누어 표현이 되니 F의 선적분은 아래와 같이 네 번의 연산을 요구합니다.

스토크스 정리를 적용하면 이것을 하나의 면적분으로 계산할 수 있습니다.(곡선 C가 둘러싼 곡면이 하나의 식으로 표현가능)

곡면 S로부터 법선벡터 N을 얻고 중적분을 수행합니다.

z = g(x,y) 형태로 곡면이 주어졌으니 xy평면으로 사영시켜 R을 설정합니다.

간단하게 표현된 면적분(중적분) 을 계산합니다.
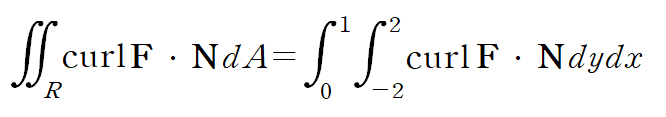



따라서 선적분 값은 -2입니다.

(예제 2) 스토크스 정리를 사용해 curl F의 S로의 면적분을 계산하여라
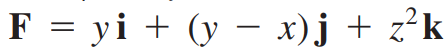
S : 중심이 (0,0,4), 반지름이 5인 구의 z >= 0인 부분
곡면 S가 xy평면의 의해 잘린 구의 일부분입니다.
F와 S가 모두 매끄러우니 단순한 선적분으로 계산할 수 있습니다.
이때 곡면을 둘러싸는 곡선 C는 반지름이 3이고 중심이 (0,0)인 xy 평면상의 원입니다.

스토크스 정리에 의해 curl F의 면적분은 폐곡선 C에 대한 선적분으로 계산할 수 있습니다.

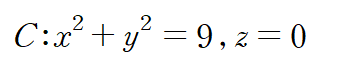

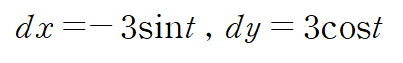

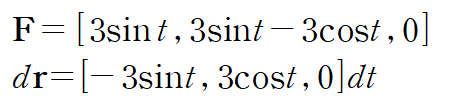


위 정적분을 계산하면 -18pi입니다.
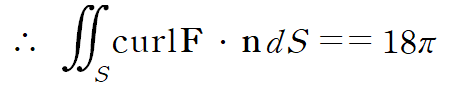
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 1.1 미분방정식의 분류 (0) | 2022.12.26 |
|---|---|
| [공업수학] 연립미분방정식 예제 : 제차 방정식 (Homogeneous Equation) (0) | 2022.12.17 |
| [공업수학] *편미분 방정식 예제 : 라플라스 변환* (0) | 2022.06.17 |
| [공업수학] 1계 상미분방정식 총정리 (2) : 동차방정식(제차방정식), u = ax+by+c 꼴 치환 (0) | 2022.03.21 |
| [공업수학] 1계 상미분방정식 총정리 (1) : 변수분리형, 완전미분방정식, 선형 상미분 방정식, 베르누이 방정식 (1) | 2022.03.19 |