1. Introduction
최소제곱법은 주어진 데이터와의 오차를 최소화하는 직선을 구하는 방법입니다.

위 그림은 주어진 5개의 데이터에 대해 두 개의 점을 지나며 오차를 줄이는 적당한 직선(linear function)을 그린 것입니다.
그러나 몇 개의 점을 지난다고 해서 오차를 완벽히 줄일 수 있는 것은 아닙니다.
2. Sum of the square errors

위 그림은 주어진 데이터(xi, yi)에 대해 그린 직선 y = f(x) 과의 오차 ei를 시각적으로 표현하였습니다.
ei 는 yi 에서 선형함수의 함숫값 f(xi) 을 뺀 것의 절댓값으로 정의됩니다.
y = f(x)가 y = ax + b 형태로 표현된다고 합시다.

이때 error(distance between the point and the graph of f) 는 아래와 같습니다.
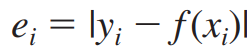
이 error 들을 제곱해 모두 더한 것을 Sum of the square errors (최소제곱합) 이라 합니다.
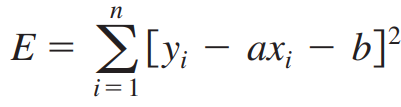
(참고)

3. Least Squares line
최소제곱합은 마치 통계에서 등장하는 편차의 제곱과 유사해보입니다.
이 최소제곱합 E가 최소가 되도록 하는 직선 y = ax + b 를 구해봅시다.
직선 y = ax + b 는 a, b 의 관점에서 볼 때 2변수 함수입니다.
a와 b에 의해 직선이 결정되고 또한 최소제곱합 또한 그 값이 변합니다.
최소제곱합이 최소가 되는 지점은 a와 b에 대한 E의 편미분계수가 모두 0이 되는 지점이어야 합니다.
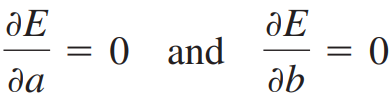
E를 편미분하여 위 두 식으로 정리합니다.
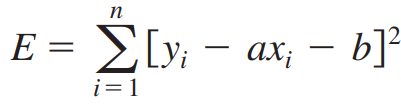
최소제곱합 E가 최소가 되게하는 두 편미분 관계식으로부터 다음 식을 얻습니다.
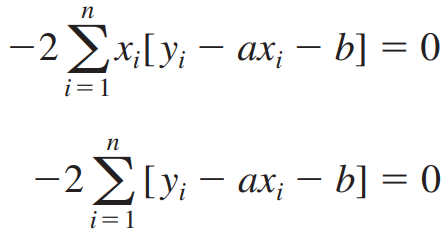
두 식을 전개해서 정리하면 다음과 같습니다.
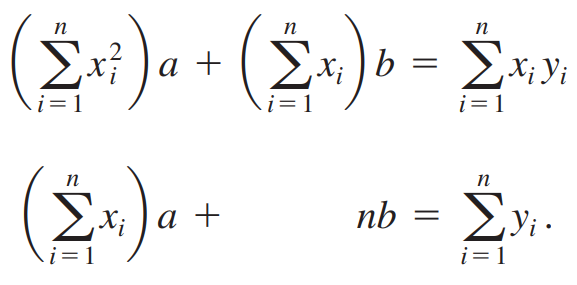
Y, A, X를 다음과 같이 설정할 때 위 식은 간단한 행렬방정식(Matrix equation)으로 변합니다.
Y는 데이터의 y값들, A는 데이터의 x값들과 크기가 n이고 모든 요소가 1인 열벡터를 나란히 놓은 것, X는 우리의 목표인 y = ax + b 의 계수입니다.
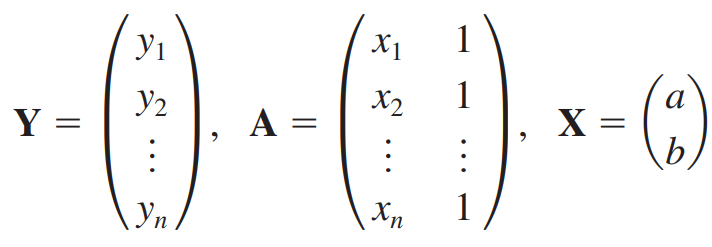

(참고)
- 좌변
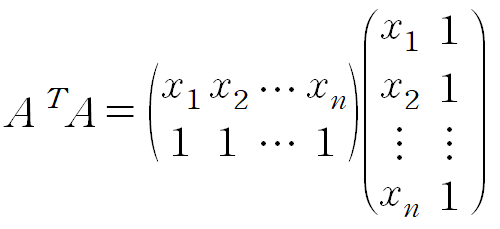
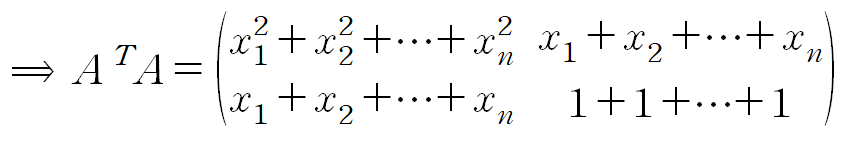
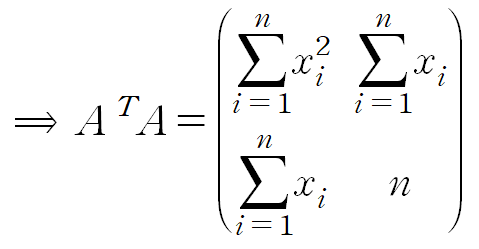
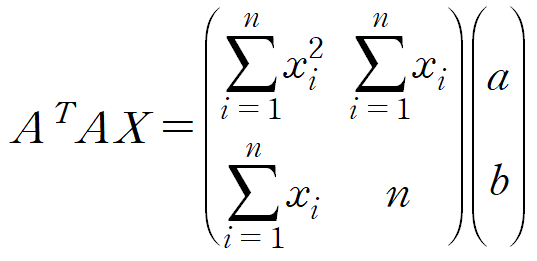
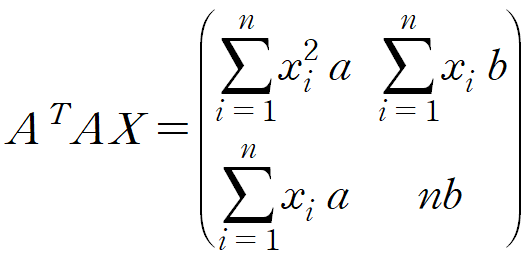
2. 우변
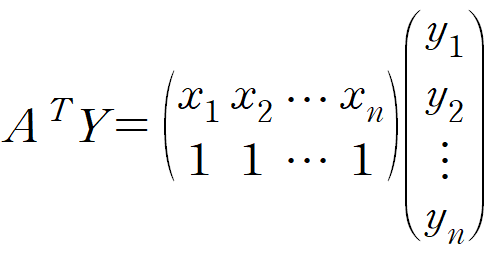

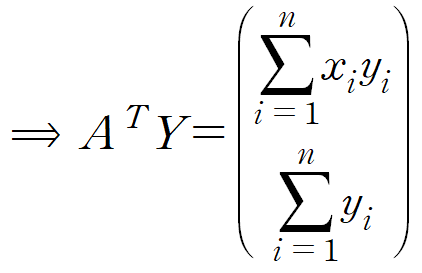

우리의 목적은 최소제곱합 E를 최소로 하는 y = ax + b를 구하는 것이었으니 x를 구하는 식을 구해봅시다.
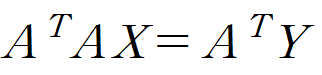

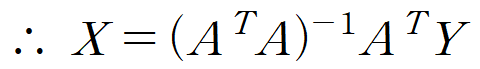
※ X는 y = ax + b 의 계수 (a,b)의 열벡터였습니다.
여기서 주의해야 하는게 우변의 괄호식을 전개하여 다음과 같이 X를 구하는 것은 명백한 오류라는 점입니다.

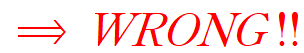

A는 n x 2 행렬이기 때문에 데이터가 두 개가 아니라면 역행렬이 정의되지 않습니다.
애초에 데이터가 두 개라면 두 점을 지나는 직선을 구하면 되기 때문에 최소제곱합으로 선형함수를 구할 일도 없습니다.
이와 같이 X를 구하는 방법을 최소제곱법(Least squares method ; Method of least squares) 이라 부릅니다.
4. Example
(예제) 주어진 다섯 개의 데이터에 대해 최소제곱법을 수행하여 선형회귀직선을 구하여라
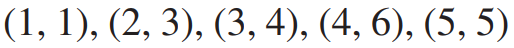
(i) 주어진 데이터들로 Y, A, X를 세팅합니다.
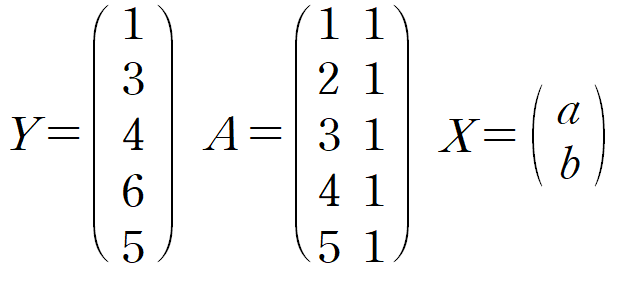
(ii) X를 계산합니다.
우리의 목표는 다음과 같습니다.

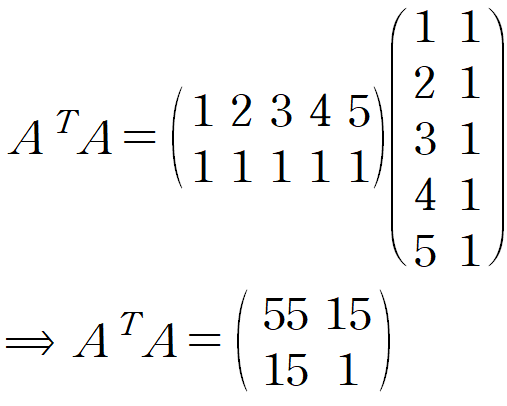
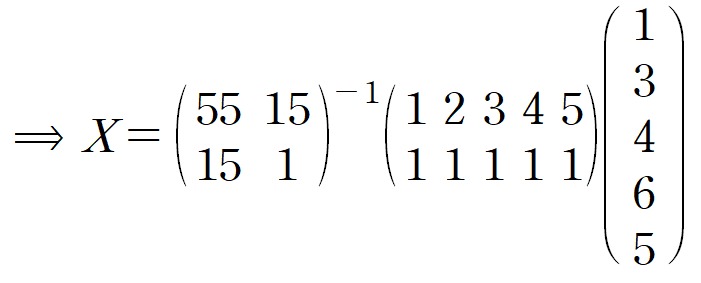
이를 계산하여 구한 X는 다음과 같습니다.
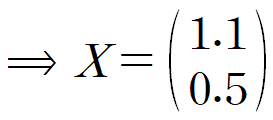
따라서 주어진 5개의 데이터에 최소제곱법을 적용해 얻은 선형회귀직선은 y = 1.1x + 0.5 입니다.


☕ 커피 한 잔보다 싼 선형대수학 모의고사 ☕
잘 공부하고 있는지 확인하실 수 있도록
기말고사를 대비할 수 있는 가벼운 모의고사를 준비했습니다.
✅ 커피 한 잔보다 싼 3,900원
✅ 총 12문제, 상세한 해설 포함 (20p가량)
✅ 문제와 해설 모두 한국어입니다.
✅ 출제단원
- 연립방정식
- LU분해
- 그람-슈미트 과정
- QR분해
- 고유값과 고유벡터
- 역행렬
- 특잇값 분해(SVD)
🚫 본 모의고사는 시험 대비 및 복습용으로 제작되었습니다.
🚫 자료의 무단 배포 및 판매 시 저작권법에 의한 처벌을 받을수 있습니다
🚫 전자책 특성 상 환불이 불가합니다.
✉️ 질문 및 기타 문의는 hyonklee@gmail.com
시험지 샘플입니다.


해설 샘플입니다.


'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 회전행렬(Rotation matrix), 회전변환 (0) | 2023.12.28 |
|---|---|
| [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지 (1) | 2023.12.12 |
| [선형대수학] 케일리-해밀턴 정리 : 행렬의 거듭제곱, 역행렬 (Cayley–Hamilton theorem) (0) | 2022.08.15 |
| [선형대수학] 그람-슈미트 과정 (Gram-Schmidt Process) 예제 (0) | 2021.12.21 |
| [선형대수학] 크래머 공식 (Cramer's Rule) (0) | 2021.11.18 |