SUBORATORY

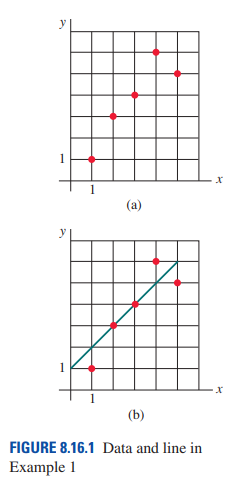
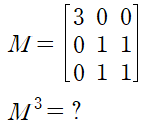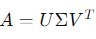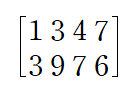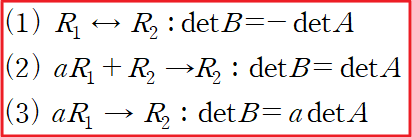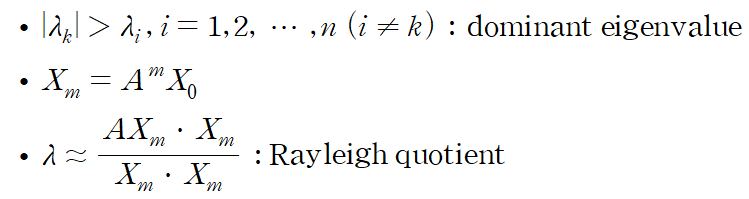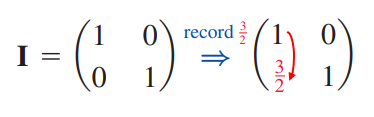#선형대수학​단위행렬 I 에 대해서는 행렬을 인수분해처럼 다뤄도 괜찮다.​어차피 행렬곱 과정에서 소거가 되기 때문인데요, 예제를 보겠습니다.​​​​(예제 1) 행렬 M에 대하여 M^3를 구하여라. 이때 행렬 M의 세제곱을 직접적으로 계산해서는 안된다. ​​​아래와 같이 행렬 M을 인수분해할 수 있습니다.​이렇게 인수분해할 수 있는 것은 단위행렬이기 때문입니다.​분해된 행렬을 계산하는 것은 비교적 간단합니다. ​따라서 M의 세제곱은 아래와 같이 계산됩니다. ​​​​​​​​이보다 더 깔끔한 상황이 있습니다.​​​​​(예제 2) 주어진 행렬을 적절한 두 행렬의 합으로 표현하여 역행렬을 구하여라Hint : 행렬의 거듭제곱 ​​ ​  ​​​먼저 A를 I+B로 분해할 수 있습니다.​이때, I+B^3은 다음과 같이 ..

#선형대수학 https://subprofessor.tistory.com/198   [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지#선형대수학 #공업수학 ​ ​ Contents - Eigenvalue(고윳값 또는 고유치) & Eigenvector - Diagonalization - Spectral Decomposition ​ ​ ​ ​ 1. Eigenvalue & Eigenvector 고윳값(또는 고유치)과 고유벡터는 정방행렬 A(squasubprofessor.tistory.com   행렬을 다른 행렬들로 분해(Decomposition)하는 방법은 다양합니다.​LU분해QR분해대각화​등등..​특이값 분해(SVD)는 대각화가 nxn 정방행렬만 가능한 것과 달리, 일반적인 mxn 행렬에 대해서 수..

#선형대수학  선형방정식에 대해 두 글에 걸쳐서 알아봤는데 이번에는 직접 선형방정식을 풀어보는 시간을 가져봅시다. 예제와 함께 풀이가 나와있긴 하지만 직접 풀고 풀이를 확인하는 것을 추천합니다​​​(예제 1) 첨가행렬로 표현된 아래 선형방정식계의 해를 구해라​​​​​ 먼저 첨가행렬을 Echelon form으로 바꾸어야 합니다​ 두 번째 행 중 가장 왼쪽에 위치한 항이 0이 되도록(정확히는 첫 번째 행에 위치한 leading entry 아래가 0이 되도록) 첫 번째 행에 -3을 곱한 것과 두 번째 행을 더하는 ERO(기초 행 연산, Elementary Row Operation)을 수행합시다Replacement​​​​​ 해를 구하기 위해서는 행렬을 Echelon form 다음 Reduced echelon f..

※2024-1 선형대수학 연립방정식 파트 모의고사 2회분 판매중입니다(3,900원)※ https://litt.ly/subprofessor 섭교수 연구소 litt.ly ​ ​ ☕ 커피 한 잔보다 싼 선형대수학 모의고사 ☕ ​ ✅ 선형대수학 연립 일차 방정식 단원 모의고사 2회분입니다. ✅ 문제는 영어, 해설은 한국어입니다. ✅ 회당 10문제, 상세한 해설 포함 (12p가량) ​ 🚫 본 모의고사는 시험 대비 및 복습용으로 제작되었습니다. 🚫 모든 문제의 저작권은 섭교수 연구소에 있으며 자료의 무단 배포 및 판매를 금지합니다. 🚫 전자책 특성 상 환불이 불가합니다. ​ ✉️ 질문 및 기타 문의는 hyonklee@gmail.com ​ 시험지 샘플입니다. ​ ​ ​ 해설 샘플입니다.

한양대 2023학년도 자연계열 수학 기출 ​ ​ 선형대수학 과목에 속한 행렬식 문제가 나왔습니다. ​ 1. Main Concept 행렬식의 성질을 이용해 크기가 큰 행렬의 행렬식을 계산하는 문제가 출제되었습니다. ​ 연립방정식의 해를 구할 때 처음 등장한 기초 행연산(기본행연산; Elementary Row Operation)이죠 기존의 행렬을 A, 기초행연산을 수행한 행렬을 B라고 하면 다음 관계가 성립합니다 ​ (1) 은 두 행의 위치를 바꾸는 interchange (2) 은 한 행에 상수를 곱해 다른 행에 더하는 replacement (3) 은 한 행에 상수배를 곱하는 scaling ​ ​ ​ ​ ​ 2. Problem 이 문제는 거기에 더해 "삼각행렬의 행렬식"이라는 개념이 추가되었습니다. ​ 왼쪽..

#선형대수학 > 미리보기 ​ ​ ​ ​ 1. Approximation of Eigenvalues 행렬의 거듭제곱(power method)을 계산하여 고유값의 근사치를 구할 수 있습니다. ​ Xm이 행렬의 거듭제곱과 어떤 벡터 X0의 곱으로 정의될 때 ​ 고유값은 다음과 같이 근사할 수 있습니다. 위 식의 우변을 Rayleigh quotient라 부릅니다. ​ 예시로 아래와 같은 2x2 행렬을 봅시다. ​ 먼저, 임의의 X0를 설정합니다. 통상적인 고유값 계산 과정은 행렬식을 이용하는 것이지만 우리는 다른 방법으로 고유값의 근사치를 구할 것입니다. ​ 연산이 많으니 가급적 간단한 X0를 사용하는 것이 좋겠죠? ​ ​ 다음으로 행렬의 거듭제곱을 사용해 적당히 큰 Xm을 얻습니다. ​ ​ 이를 반복해 X7까지..

#선형대수학 2차원 평면에서 반시계방향으로 θ만큼 회전한 회전행렬은 다음과 같이 표현된다 ​ ​ 열벡터 형태로 표시된 [x,y]를 이 행렬에 곱하면 반시계방향으로 θ만큼 회전이 된다. ​ 여기서 [x,y]가 의미하는 것은 점이 될 수도 있고, 도형이 될 수도 있다. ​ ​ ​ ​ 이것을 사용해 이차곡선을 회전시킬 수도 있다. ​ ​ 위 타원을 반시계방향으로 45도 회전한 도형의 방정식을 구해보자 ​ 먼저 회전행렬을 정의하고 ​ 그 다음 회전 변환 식을 이용해 ​ x', y' 에 대한 식을 얻는다. ​ 우리가 가지고 있는 것은 x, y에 대한 관계식(타원의 방정식)이므로 ​ x와 y에 대해 식을 정리해서 넣어주자 ​ ​ 타원에 방정식에 정리한 x, y를 넣어주고 정리하면 ​ 아래와 같은 식을 얻는다. ​ ..

#선형대수학 #공업수학 ​ ​ Contents - Eigenvalue(고윳값 또는 고유치) & Eigenvector - Diagonalization - Spectral Decomposition ​ ​ ​ ​ 1. Eigenvalue & Eigenvector 고윳값(또는 고유치)과 고유벡터는 정방행렬 A(square matrix, n x n)에 대해 아래 식을 만족하는 상수 λ(lambda, 람다)와 그에 대응되는 영벡터가 아닌 벡터 v를 말한다. ​ * 고유벡터는 0이 아니어야 하지만 고윳값은 0일 수 있다. * 각 고유벡터는 앞서 구한 고윳값에 "대응"된다. ​ 위 정의식을 조금 변형하여 고윳값과 고유벡터를 구할 수 있다. ​ 세 번째 줄의 행렬 방정식(벡터 v에 대한 방정식)이 0이 아닌 해를 가져야..

https://search.shopping.naver.com/book/catalog/32487155058 Linear Algebra and Its Applications, Global Edition : 네이버 도서 네이버 도서 상세정보를 제공합니다. search.shopping.naver.com ​§ 목차 § 0. LU분해 소개 1. LU분해 2. LU분해 알고리즘 3. 파이썬 구현 4. LU분해로 행렬방정식의 해 구하기 5. LU분해로 행렬식 계산하기 ​ ​ ​ ​ 0. Introduction LU분해는 행렬 분해의 한 종류입니다. L은 Lower triangular matrix(하삼각행렬), U는 Upper triangular matrix(상삼각행렬)을 의미합니다. 또다른 행렬 분해로는 직교행렬과 상..

#선형대수학​ 1. Introduction 최소제곱법은 주어진 데이터와의 오차를 최소화하는 직선을 구하는 방법입니다.​ ​​ 위 그림은 주어진 5개의 데이터에 대해 두 개의 점을 지나며 오차를 줄이는 적당한 직선(linear function)을 그린 것입니다.​ 그러나 몇 개의 점을 지난다고 해서 오차를 완벽히 줄일 수 있는 것은 아닙니다.​ ​​​2. Sum of the square errors​ ​    위 그림은 주어진 데이터(xi, yi)에 대해 그린 직선 y = f(x) 과의 오차 ei를 시각적으로 표현하였습니다. ei 는 yi 에서 선형함수의 함숫값 f(xi) 을 뺀 것의 절댓값으로 정의됩니다.​​ y = f(x)가 y = ax + b 형태로 표현된다고 합시다.​ 이때 error(distanc..