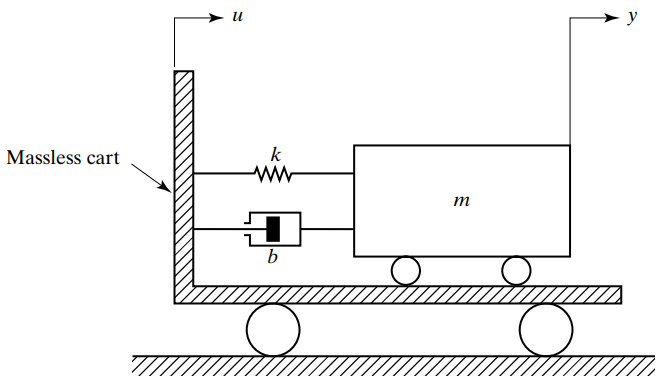
#동역학 #시스템해석 https://search.shopping.naver.com/book/catalog/32464065666 System Dynamics : 네이버 도서 네이버 도서 상세정보를 제공합니다. search.shopping.naver.com 1. State Equation & Output Equation (1) State Equation (2) Output Equation > 용어설명 x : State Vector u : Input Vector y : Output Vector A : State Matrix (A matrix) B : Input Matrix (B matrix) C : Output matrix (C matrix) D : Direct Transmissi..