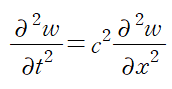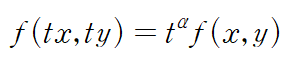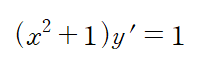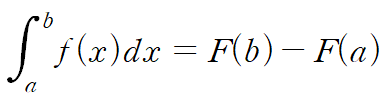SUBORATORY

#공업수학 #라플라스변환 #편미분방정식 ​ ​ 지난 시간에 이어 편미분 방정식 예제를 풀어봅시다. 편미분방정식을 라플라스 변환으로 푸는 기본개념은 아래 링크 참조 바랍니다. ​ ​ https://subprofessor.tistory.com/17 [공업수학] 6. 편미분 방정식 : 라플라스 변환 해법 이전에 포스팅한 라플라스 변환은 f(t)에 관한, 즉 일변수 t에 대한 상미분방정식을 풀기 위한 해법으로써 소개되었다. 대수방정식을 거쳐 해를 구한다는 다소 편리한 이 라플라스 변환은 상미 subprofessor.tistory.com ​ ​ (예제) ​ ​ ※1차원 파동방정식의 모델링은 생략하겠습니다※ ​ 지난 번에 설명했듯, 경계조건(Boundary Condition)은 정의역(위 문제에서는 x)의 경계에서..

수학 가형과 나형에서 공통적으로 「실수 전체에서 미분가능한 함수 f(x)」 라던지, 「f(x)가 실수 전체에서 미분가능할 때」 같은 문장이 종종 등장한다. 공부를 제대로 하지 않은 학생은 이 문장을 그냥 "이 말은 맨날 나오네 문제 분량 채울 게 없나봐?" 혹은 "당연한 거 아냐? 어쩌라고!" 라고 생각하고 넘어가거나 생각조차 하지 않고 그냥 넘어가버린다. 하지만 이 문장은 정말 정말 정말 정말 중요한 문장이다. 문제를 푸는 어떤 "길"이 있다고 하자. 답으로 이르는 이 "길"은 중간중간에 답까지 잘 찾아갈 수 있도록 하는 중간중간에 "조건"이라는 장치가 있다. 일종의 표지판의 역할을 하는 "조건"을 찾지 못한다면 답까지 도달할 수 없다. "조건"들은 문제 곳곳에 처음부터 끝까지 보물찾기 마냥 숨어있다...

지난 시간에 이어 수학 가형에서 제시해주는 '미분가능'조건을 어떻게 해석해야 좋은가를 알아보자. 솔직히 나형처럼 구간을 나눠서 미분가능->연속조건을 사용하는 호락호락한 문제는 그렇게 많지 않다. 오히려 미분가능하다는 것이 무엇인지 그 정의에 대해 알고있어야 하는 경우가 많다. 가형에서 미분가능 조건이 제시되는 경우는 최근 기출을 봤을 때 합성함수의 미분, 역함수의 미분이 자주 출제되고, 가끔 고난도문제에서 절댓값기호가 포함된 함수의 미분 정도? 일단 기출을 통해 어떤 방식으로 출제되는지 알아보자 ​ ​ ​ 2021학년도 6월 수학가형 11번 ​ 2020학년도 수능 수학가형 17번 ​ 2020학년도 수능 수학가형 21번 ​ 2020학년도 수능 수학가형 26번 ​ 2020학년도 9월 수학가형 17번 ​ 20..

#공업수학 ​ 이전 글에서 1계 미방은 네 가지만 알면 된다고 했는데 추가로 지금까지 블로그에서 다루지 않은 두 가지 형태를 더 소개합니다. ​ (1) Homogeneous Equation 실수 α 에 대해 위 꼴로 정리되는 함수 f(x,y)를 동차함수(homogeneous function)이라 합니다. ​ 아래와 같은 미분방정식에 대해 ​ M과 N이 모두 동차함수인 것을 동차미분방정식 이라 합니다. ​ ​ ​ dx 앞에 붙은 함수의 동차성 검증 ​ dy 앞에 붙은 함수의 동차성 검증 ​ 위 방정식의 경우 M(x,y)와 N(x,y) 가 모두 2차 동차함수(homogeneous function of degree 2) 라 부릅니다. ​ 만약 M과 N이 모두 동차함수이며 그 차수가 동일하다면 u = y/x 또..

ㄴ #공업수학 ​ 1계 상미분방정식은 네 가지 형태만 알면 됩니다. P(x)dx = Q(y)dy 꼴로 표현가능한 변수분리형과 M(x,y)dx + N(x,y)dy = 0 꼴의 완전미분방정식, y' + P(x)y = r(x) 꼴인 선형 상미분 방정식, y' + p(x)y = r(x)y^a 꼴의 베르누이 방정식. ​ ​ (1) 변수분리형 https://blog.naver.com/subprofessor/222094390913 [공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식) 드디어 시작이다. 간단한 변수분리형 1계 상미분 방정식을 풀어보자. 1.2는 방향장(direction field)에 관... blog.naver.com ​ ​ 위와 같이 각 변수로만 묶이도록 양변을 정리하여 적분할 ..

정적분의 값을 구하는 방법은 피적분함수의 원시함수(역도함수, Antiderivative)를 구해 구간의 끝 값을 대입하는 것입니다. ​ 이를테면 처럼 ​ 그런데 일반적인 방법으로 Antiderivative를 구할 수 없는 함수에 대해서는 정적분을 어떻게 구해야 하는가? 라는 물음이 생겨나는데 아래와 같은 경우를 살펴봅시다. ​ 마땅한 Antiderivative를 구하기가 어렵습니다. 해서 f(x)와 근접한 다항함수 P(x)를 찾아 그것의 정적분으로 f(x)의 정적분 값을 근사하는 것이 뉴턴-코츠 공식입니다. ​ ​ ​ 1. 사다리꼴 (Trapezoidal Rule) 작은 도형으로 쪼개서 그 넓이를 구한다. 라는 개념은 고등학교 과정에서도 배우는 구분구적법 내용입니다. ​ 사다리꼴 공식은 각 점을 잇는 선..

그린정리는 폐곡선 C를 경로로 취하는 선적분(Line Integral)과 C로 둘러싸인 영역 D의 중적분(Double Integral) 간의 관계를 부여하는 정리라고 할 수 있습니다. 정리를 소개하기 이전에 곡선 C의 양의 방향(positive orientation)을 시계반대방향(counterclockwise, CCW)으로 정의하겠습니다. ​ 1. 그린정리 (Green'sTheorem) ​ 보통은 C가 폐곡선이기 때문에 아래와 같은 식으로 그린정리를 소개합니다. D는 앞서 소개했듯이 C로 둘러싸인 영역입니다. ​ ​ 그린정리를 간단히 설명하자면 다음과 같습니다. ​ 곡선 C가 매끄럽고 양의 방향을 가지며 평면 상의 폐곡선일 때 C로 둘러싸인 영역을 D라고 하자. 이때 F = 로 표현되는 벡터함수다. ​..

그람-슈미트 과정은 임의의 벡터 집합으로부터 직교집합(Orthogonal set)을 구하는 과정입니다. 원래 가지고 있던 벡터 집합의 직교성 유무와 관계없이 한 벡터를 다른 벡터에 사영(projection)시킨 것을 이용해 직교집합을 구할 수 있습니다.​  ​​1. 그람-슈미트 과정 (Gram-Schmidt Process)​ 그람-슈미트 과정의 정의는 다음과 같습니다.​ 부분합 기호(시그마)를 이용해 나타내면 다음과 같습니다.​ 부분공간 W를 이루는 기저를 직교기저(Orthogonal basis)로 변환하는 것이 그람-슈미트 과정의 의의입니다. 이때 그람-슈미트 과정을 수행하기 전의 기저와 수행하고 난 이후의 기저가 이루는 생성집합(span)은 각각 부분공간 W와 같습니다. ​​​​2. 예제 ​(예제 1..

복소평면 z = x+yi 에서의 선적분과 관련된 코시 적분에 대해 알아봅시다. ​ 1. Cauchy's Integral Theorem ​ 코시적분정리는 f(z)가 D에서 해석적이라면 Simple closed path C에 대한 선적분이 항상 0이 된다는 뜻입니다. 여기서 simple closed path 라는 것은 경로가 교차하거나 맞닿는 지점이 없는 것을 의미하고 simply connected domain 이라는 것은 구멍이 없는 영역이라고 생각하면 됩니다. 구멍이 없을 경우 하나의 선으로 연결된 영역이 됩니다. ​ ​ 코시적분정리에 따라 Simply connected domain 에서 Simple closed path C에 대한 아래 선적분들은 모두 0입니다. ​ ​ ​ 추가적으로 domain에 구멍..

지난 시간 소개한 라그랑주 다항식에 이어 뉴턴 보간법과 분할차분(Divided Difference)에 대해서 알아봅시다. ​ https://subprofessor.tistory.com/63 [수치해석학] 라그랑주 다항식 (Lagrange Polynomial), 파이썬 코드 오늘 다룰 내용은 보간법의 일종인 라그랑주 다항식 입니다. 보간법(Interpolating)은 간단히 몇 개의 점이 주어졌을 때 그것을 관통하는 함수를 세워 discrete한 데이터들을 연속적인 데이터로 근사 subprofessor.tistory.com 보간법에 대한 설명은 위 링크로 대체하겠습니다. ​ 1. Newton's Interpolating Polynomial 뉴턴 보간법은 다음과 같은 형태의 Polynomial 을 지칭합니다..