반응형
#공업수학
푸리에 변환과 푸리에 역변환은 다음과 같습니다.
1. 푸리에 변환
푸리에 변환은 다음과 같이 정의됩니다.

푸리에 변환의 경우 적분구간이 (-∞,∞) 이고 코사인, 사인 변환의 경우 (0,∞)라는 것에 주의합니다.
푸리에 역변환에 있는 1/2π 항을 루트로 나눠서 푸리에 변환과 역변환에 각각 나누어 정의하기도 합니다(크레이지 공업수학)
2. 도함수 공식
편미분 방정식을 푸는 데 라플라스 변환을 사용하는 것처럼 푸리에 변환을 사용할 수도 있습니다.
*참고*
[공업수학] *편미분 방정식 예제 : 라플라스 변환*
#공업수학 #라플라스변환 #편미분방정식 지난 시간에 이어 편미분 방정식 예제를 풀어봅시다. 편미분방정식...
blog.naver.com
도함수에 관한 푸리에 변환은 다음과 같습니다.


푸리에 코사인, 사인 변환에 대한 도함수 공식입니다.
> 1계 도함수

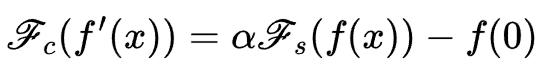
> 2계 도함수


유도는 부분적분을 통해 할 수 있습니다.
예시로 사인 변환의 2계 도함수 공식을 유도해보겠습니다.

반응형
3. 편미분 방정식 적용 시 유의사항
편미분 방정식에 푸리에 변환을 적용하려면 아래 사항들을 유의하여 사용해야 합니다.
(1) 어떤 변수에 대해, 어떤 푸리에 변환을 수행하는지 정의할 것
(2) 푸리에 변환을 수행하는 변수의 정의역 확인하기
▷ (-∞,∞) : 푸리에 변환
▷ (0,∞) : 푸리에 코사인 변환 / 푸리에 사인 변환
▶▶ 2계 편미분 방정식의 경우 초깃값이 뭔지에 따라 코사인 / 사인 변환을 사용
▶▶ f(0) → 푸리에 사인 변환, f'(0) → 푸리에 코사인 변환
반응형
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 1.4-1 완전미분방정식(Exact ODEs) (0) | 2022.12.29 |
|---|---|
| [공업수학] 편미분 방정식 (1) : 변수분리부터 푸리에 변환까지 (2) | 2022.12.27 |
| [공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식) (0) | 2022.12.27 |
| [공업수학] 1.1 미분방정식의 분류 (0) | 2022.12.26 |
| [공업수학] 연립미분방정식 예제 : 제차 방정식 (Homogeneous Equation) (0) | 2022.12.17 |