반응형
1. Definition
다변수함수에서 x, y, z 에 대한 편미분도 가능하지만 임의의 벡터를 기준으로 도함수를 구할 수도 있습니다.
이것을 방향도함수(Directional Derivative)라 부르며 다음과 같이 정의됩니다.

점 P에서 f(x,y,z)의 벡터 b 방향으로의 방향도함수 Dbf 또는 df/ds 는 식 (2)와 같이 정의됩니다.
이때 Q는 P를 지나며 b를 방향벡터로 갖는 직선 L에서 P로 다가가는 움직이는 점이고 s는 P와 Q사이의 거리입니다.
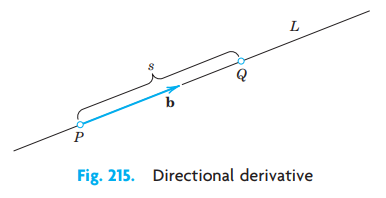
방향도함수의 계산은 gradient 를 이용합니다. 이때 b는 단위벡터입니다.

임의의 크기를 가지는 벡터에 대한 방향도함수의 계산은 벡터의 크기로 나누어주는 것으로 정의됩니다.
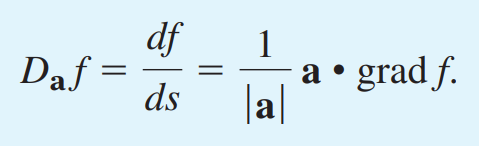
다음과 같이 정의되기도 합니다.
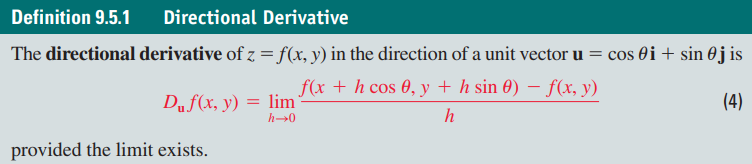
b 대신에 임의의 단위벡터 u를 사용하고 s 대신에 h를 사용해 정의했습니다.
이는 z = f(x,y)라는 특수한 경우에만 적용되는 정의입니다.

역삼각형 기호(▽) 는 gradient입니다.
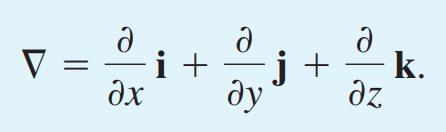
※ 방향도함수는 내적값이기 때문에 scarlar 입니다.
2. Examples
(예제) 주어진 f(x,y,z)와 점 P(2,1,3)에 대하여 a = [1,0,-2] 방향으로의 방향도함수를 계산하여라

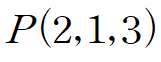
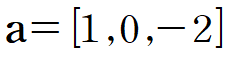
주어진 방향벡터가 단위벡터가 아니므로 아래 식을 사용합니다.

gradient 를 구하고 P(2,1,3) 점 x=2, y=1, z=3 을 대입합니다.
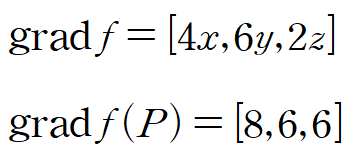
따라서 P점에서 a방향으로의 방향도함수는 다음과 같습니다.
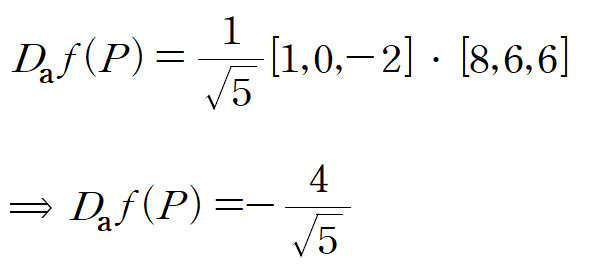
반응형
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 삼각함수 어려운 적분(Trigonometric Integrals), 삼각 적분 (0) | 2023.08.03 |
|---|---|
| [미분적분학] 회전체 부피 구하기 : 디스크, 원통셸 방법 (4) | 2023.01.10 |
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.23 |
| [미분적분학] 라그랑주 승수법 예제 (0) | 2021.12.12 |
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.10 |