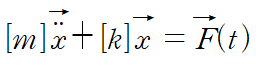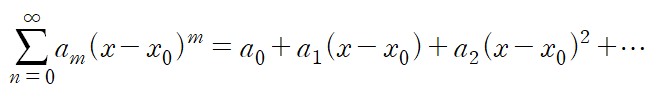SUBORATORY

#기계진동 orthogonality와 eigen analysis에 관한 자세한 내용은 생략하고 어떤 식으로 다자유도계 비감쇄 진동 문제를 풀어나가는지 예제를 중심으로 알아봅시다. ​ Multi Degrre of Freedom System을 줄여 M-DOF 문제 라고도 하는데 M-DOF 문제에서 중요한 것은 modal matrix를 구하는 것입니다. modal matrix를 구한 후 이를 이용해 초깃값을 변환하고 변환된 해를 다시 역변환 하여 최종적인 해를 구성하는 것이 기본적인 흐름입니다. ​ 이 글에서는 감쇄(Damping)가 없는 비감쇄 문제(Undamped System)만을 다루며 강제진동(Forced Vibration) 예제를 풀어보겠습니다. ​ ​ ​ 1. 다자유도계 문제를 푸는 순서 다자유도계..

#공업수학​ ​ 0. Introduction ​ 멱급수란 다항함수들의 합으로 구성된 급수를 뜻하며 앞서 테일러 급수를 통해 함수를 멱급수 형태로 나타내는 방법을 소개했었다. https://blog.naver.com/subprofessor/222106300471 [미분적분학] 테일러 급수전개 #미분적분학 테일러 급수전개는 미분방정식을 공부하면서도 나오는 내용이고, 어떤 값을 근사하는 데도 사... blog.naver.com ​ ​ 아래와 같은 형태의 급수를 멱급수라 한다. 가장 일반적인 형태이며 우리는 x0 = 0 즉, x = 0에서 전개한 멱급수를 사용할 것이다. ​ ​ ​ 지수함수를 아래와 같이 표현할 수도 있고 ​ 유리함수를 표현할 수도 있다. ​ 물론 수렴범위가 무한한 것은 아니다. 위 유리함수의 ..

#재료과학 #재휘현상 ​ ​ 금속을 액체 상태에서 고체 상태로 냉각하는 과정(Solidification)은 여러가지 요인들에 의해 조절됩니다. 냉각 속도와 온도 차 등 여러 요인들 중에서 접종 여부(고체 불순물이 잘 분포되어 있는가)는 가장 중요한 요인으로 취급됩니다. ​ 순수한 물과 작은 고체 불순물을 포함한 물 두 가지 중 더 빨리 어는 것은 놀랍게도 후자입니다. 액체가 고체로 변하는 것은 작은 고체입자가 만들어지는 것부터 시작하는데 그것은 보통 고체 벽 또는 이미 존재하는 고체 불순물에서부터 자라기 때문이죠 ​ ​ ​ ​ ​ 재휘현상은 접종이 잘 이뤄지지 않은 상태에서 냉각시 발생하는 현상입니다. 냉각 과정 중 갑자기 열이 방출되며 액상(액체)의 온도가 상승하게 되는데 이 때의 방출되는 열을 "용융..

#통계학 #가설검정 유의확률 유의확률은 유의수준과 관련이 있는 값이다. 유의확률의 정의는 "영가설을 기각할 수 있는 유의수준의 최솟값"이고, 유의수준은 α = 0.05 -> 신뢰수준 95%임을 의미 ​ 지금까지는 가설검정을 "검정통계량"이 기각역에 포함되는지로 확인했는데 p-value 또는 유의확률이라 불리는 통계량을 사용할 수도 있다. ​ 유의확률은 단순히 "기각역의 확률"이라고 받아들일 수도 있다. 또는 검정통계량이 기각역에 속할 확률. ​ 예를 들어 모분산이 알려진 우측 단측 검정에서 영가설 H0 하에서 검정통계량이 T0 = 1.5 였다면 유의수준 0.05에서 기각역은 ​ C = {T0 > 1.645} 이다. (검정통계량은 이때 표준정규분포를 따름; T0~N(0,1)) ​ 유의확률(p값 ; p-va..

#수치해석 ​ Runge-Kutta Method 룽게 쿠타 방법은 초깃값 문제, 즉 아래와 같은 미분방정식을 푸는 수치해석 기법이다. ​ 아래와 같은 미분방정식을 룽게 쿠타 방법으로 풀 수 있다. ​ ​ ​ 오일러 방법(Euler's method), 호인의 방법(Heun's method), 중간점 방법(Midpoint method) 등의 미분방정식을 푸는 여러 가지 기법은 대부분 이 룽게-쿠타 방법의 일종이다. ​ RK method는 선형 미분방정식이 아니라 비선형 미분방정식에도 적용할 수 있다는 매우 큰 장점이 있다. ​ ​ ​ ​ 다음과 같은 방법을 Runge-Kutta Method라고 한다. ​ ​ 여기서 h는 step size이고 ​ φ(phi) 는 함숫값들로부터 계산되는 어떤 값이다. 원하는 만..

#유체역학 파이프 유동 문제는 관의 형상(지름, 길이), 관의 재질(거칠기, 마찰), 압력 차이가 주된 관심사입니다. ​ 파이프 유동은 internal flow의 대표적인 예이며 유체의 유동을 유발하는 주된 원인이 두 지점의 압력차이가 됩니다. ​ 때문에 내가 A지점에서 B지점까지 유체를 수송하려 할 때 얼마만큼의 압력차이가 요구되는가?라는 것이 설계의 주된 목적이 되며 관의 형상은 유량에 변화를, 관의 재질과 형상은 유동 중 손실되는 에너지에 변화를 줍니다. ​ 때문에 에너지 방정식을 수립하고 상황을 잘 파악해서 식을 잘 정리한다면 어려울 게 없습니다. 파이프 유동에서 가장 복잡한 축에 속하는 문제는 여러 개의 관이 연결된 유동과 난류유동에서 달시 마찰계수 f를 trial and error로 찾는 문제..

#라플라스변환 라플라스 변환과 관련된 공식과 라플라스 변환의 성질들을 모아놓은 글입니다. ​ 출처 : Feedback Control of Dynamic Systems, Gene Franklin ​ ​ (1) 라플라스 테이블 Feedback Control of Dynamic Systems, Gene Franklin ​ ​ ​ ​ ​ ​ ​ (2) 라플라스 변환의 성질 Feedback Control of Dynamic Systems, Gene Franklin ​ ​ 1. 중첩원리 2. t-shifting(t-이동정리) 3. 치환적분 4. s-shifting(s-이동정리) 5. f(t)의 미분 6. f(t)의 적분 7. 합성곱(convolution). F(s)G(s) 역변환 가능 8. 초깃값 정리(IVT) 9..

#열역학 ​ Maxwell Relations 맥스웰 관계식은 네 가지 열역학 변수들에 대한 네 개의 관계식입니다. ​ ​ ​ ​ Example (예제 1) 다음 관계식을 이용하여 (∂T/∂v)s 를 유도하여라 ​ ​ ​ ​ 먼저, 유도해야 하는 식에서 s가 일정하다고 하니 ds = 0입니다. ​ ​ ​ 양변을 dv로 나누고 좌우변을 잘 정리하면 다음과 같이 원하는 관계식을 얻습니다. ​ ​ 문제의 요구사항과 어떤 변수가 상수인지를 먼저 확인하고 필요하다면 적절한 맥스웰 관계식을 사용해주어야 합니다. ​ ​ ​ ​ (예제 2) 깁스 관계식 du = Tds - Pdv 와 맥스웰 관계식을 이용해 P,v,T로만 표현된 (∂u/∂P)T 를 유도하여라. 또한 이상기체에서 이 편도함수가 어떤 거동을 보이는지 확인하여..

#유체역학 ​ ​ 유체가 파이프 내부를 지나갈 때 벽면과의 마찰 때문에, 또는 관이 꺾이거나 관의 형상이 바뀌는 지점(갑자기 좁아지는)에서 유체가 가진 에너지의 손실이 발생합니다. ​ 이때의 손실을 Major loss와 minor loss 로 구분하며 이번 게시글에서는 Major loss를 다룹니다. ​ ​ 1. Darcy Friction Factor Major loss는 유체와 파이프의 마찰 때문에 발생하는 손실이며 다음과 같이 수두(head)형태 즉 미터 단위(또는 ft, in) 로 표현됩니다. ​ 위 식을 "Darcy-Weisbach equation" 이라 합니다. ​ f는 darcy friction factor, l은 관의 길이, D는 관의 직경, V는 관을 지나는 유체의 속도(평균속도), g는 ..

#열역학 ​ Maxwell Relations 맥스웰 관계식은 압력(P), 비체적(v), 온도(T), 엔트로피(s) 사이의 관계를 나타내는 4가지 관계식이다. ​ 내부에너지(u)와 엔탈피(h)의 exact differential 에서 (1), (2) 식을 얻고 ​ Helmholtz function(A) 로부터 (3) 식을, ​ Gibbs function(G) 로부터 (4) 식을 얻는다. ​ ​ 이것이 모두 exact differential 이므로 우변에 존재하는 두 개의 미분소의 계수에 대해 다음이 성립한다. ​ ​ ​ 즉 (1),(2),(3),(4) 각각에 대해 이 성질을 적용할 수 있다. ​ ​ 위 네 가지 식이 바로 맥스웰 관계식이다. ​ ​ ​ Applications 맥스웰 관계식은 편미분방정식에서..