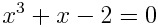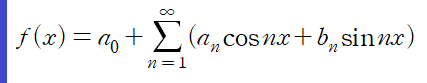SUBORATORY

오늘은 Erwin Kreyszig 의 Advanced Engineering Mathematics 에 수록된 선적분 예제를 풀어보자 ​ PART 1) 일반적인 선적분 계산 를 구하여라 ​ ​ (예제 1) ​ ​ ​ ​ (예제 2) ​ ​ ​ ​ ​ ​ (예제 3) ​ 곡선 C는 위와 같다 ​ ​ ​ ​ PART 2) C가 폐곡선인 경우 를 구하여라 ​ (예제 1) ​ ​ 경로를 매개변수 t 로 나타내면 아래와 같다 ​ 곡선 C가 폐곡선이므로 선적분은 폐곡선에 대한 선적분이다 ​ 사실 그린정리나 스토크스 정리 등이 아니라 일반적인 선적분 계산 문제에서는 폐곡선이냐 아니냐가 딱히 중요하지 않습니다. 생긴것만 저렇게 생겼지 동일한 방법으로 계산합니다 ​ ​ ​ ​ PART 3) F가 경로 독립(Path Inde..

사실 공업수학에서 미분방정식의 해를 구하기 위해 사용하는 방법이지만 별도로 미분적분학에 먼저 포스팅한다. ​ 라플라스 변환은 미분방정식을 대수방정식 꼴로 변환시켜 보다 쉬운 방정식을 풀 수 있다는 이점을 가지고 있는 변환법이다. ​ 대수방정식은 이런 애들을 칭하는 말이다. 대수적인 특성을 가지고 있는 방정식을 의미하며(당연히..) 사칙연산을 통해 해를 구할 수 있는 방정식을 의미한다. 미분방정식은 미분개념과 적분개념이 모두 포함되어 있는 방정식인데, 이 방정식은 애초에 사람이 인지하기가 어렵다. 변화율을 인지하는 것 자체가 어렵기도 하고 지수함수나 삼각함수와 같은 초월함수들이 포함될 경우 더더욱 이해하기가 어렵다. 반면 대수방정식은 인수분해 또는 근의 공식을 통해 쉽게 해를 구할 수 있다는 장점이 있다...

푸리에 급수란? 푸리에 급수(Fourier Series) 는 삼각함수들의 합으로 주기함수를 나타내는 방법이다. 나중에 푸리에 적분에서는 주기함수라는 조건이 무의미해지는 지경까지 이른다.(주기를 무한대로 잡은 것..) "대체 이걸 어떻게 떠올린 거지?"라는 생각이 안 날 수가 없는 위대한 발견이다. 푸리에 급수는 파동분석을 하기 위한 기초 개념이다. 푸리에 변환은 주기함수건, 비주기함수건 상관없이 삼각함수의 합 꼴로 함수를 해석할 수 있게 도와주는 도구다. 파일 압축에도 사용된다는데 거기까지는 아직 내 분야가 아니라 Pass.. 우리의 목표는 푸리에 변환까지다. 아무튼 이 "푸리에 XX"를 통틀어 푸리에 분석(Fourier Analysis)이라고 부른다. 아무튼 그 푸리에 분석의 기초가 되는 '푸리에 급수..

이건 스칼라함수고 이건 벡터함수다. (i) 벡터함수의 미분 오늘은 벡터함수의 미분에 대해 알아봅시다. 우리가 고등학교과정까지 배우는 함수는 100% 스칼라함수입니다. 결괏값이 스칼라이면 스칼라함수, 결괏값이 벡터이면 벡터함수라고 취급합니다. 스칼라 함수의 미분은 다들 알듯이, 다음 정의를 이용합니다. 벡터함수의 경우에도 같은 방법으로 미분을 해주고 뒤에 단위벡터를 붙여주면 됩니다. 별 거 없어요. 도입부에 소개한 벡터함수를 미분해보면 다음과 같습니다. 단위벡터는 상수같은 느낌으로 다뤄주시면 됩니다. 상수같은 느낌? 그렇다면 벡터함수가 단위벡터의 상수배로 주어졌을 때는 어떻게 미분하면 될까요? 네 스칼라함수일 경우와 같이 r'(t)=0이 됩니다. 벡터함수의 미분 정의는 다음과 같습니다. 이때, r(t)는 ..

미분방정식이란 말은 왠지 모르게 멋있다. 고등학교 들어와서 '미분방정식'푸는 공대 형들이 참 멋있어보였다. 나만 그런가..? 아무튼, 실제로 미분방정식은 "멋있다." 자동차를 굴리는 힘인 엔진에서도 미분방정식을 빼놓고 설명할 수 없으며 바짓주머니 속에 있는 스마트폰에서도, 릴라드가 던진 클러치 3점슛에서도 미분방정식은 등장한다. 공업수학을 배우고 나면 사회 전반에 미분방정식이 관여하고 있음을 깨닫는다. 도대체 미분방정식이란 게 뭘까? (i) 미분방정식? 미분방정식이라는 건 [미분]+[방정식] 같은 느낌으로 이해하면 된다. 고등학교 때 배우는 미적분과 초등학교 때 배우기 시작하는 방정식의 '역대급' 콜라보랄까? 한창 과외를 할 때 방정식의 정의를 모르는 학생들을 참 많이 만났다. 방정식의 정의는 다음과 같..

공업수학 포스팅은 Erwin Kreyszig 의 Advanced Engineering Mathematics 10th edition 즉 공업수학 10판을 기반으로 하며 상미분 방정식만을 다룬다. 교재의 로드맵을 이용해 보여주면 다음과 같다. 기회가 되면 PART B도 포스팅할 것 같은데 일단 계획은 상미분 방정식까지만. 편미분 방정식부터는 너무 괴랄하고 복잡한 데다가 필요한 사람의 풀(pool)이 너무 좁아지기 때문에 굳이 포스팅하지 않는다. (사실 내가 잘 몰라서_.._) 포스팅 목적 자체가 일반인들도 마치 잡지 읽듯이 부담감 없이 읽을 수 있도록 '소개'하는 것 그리고 쉬운 설명이 필요한 전공인들에게 '이해'를 돕는 것에 있기 때문에 PART A까지만 포스팅한다. 상미분 방정식을 푸는 방법에는 크게 세..

코로나 19가 한창 유행하던 3월 말 이후로 주식투자를 통해 큰 수익을 올렸다는 얘기들이 곳곳에서 들려온다. 쌀 때 사고 비쌀 때 판다는 통상적인 "투기 전략"으로 주식시장에 임한 사람들이 성공담의 주를 이뤘다. 나는 이것이 잘못되었다는 걸 솔직히 몰랐다. 투자를 그저 "쉽게 돈 버는 수단"중의 하나로 생각했을 뿐이다. 지금은 쉽게 돈을 벌고자 했다는 것을 순순히 인정하지만 과거에는 뭔가 떳떳하지 못한 마음에 가족에게도, 주변 사람들에게도 알리기 꺼려졌던 주식투자였다. 보이지 않던 길을 보이게 하는 사람이 계몽가라면 존 리는 그 칭호를 사용함에 부족함이 없는 사람이다. 계몽가 존 리의 목적은 단 하나다. 한국인들이 금융 문맹으로부터 경제독립으로 갈 수 있도록 돕는 것. 그 첫 출발은 2014년 미국에서 ..

돈이 인생의 전부는 아니라는 말에 많은 사람들이 동의하고 살아가지만 실제로는 인생 대부분의 시간을 돈을 벌기 위해 할애한다. 돈이 많다고 행복한 건 아니지만 행복하기 위해선 돈이 필요하다는 말은 우리 주변에서 자주 볼 수 있는 아이러니이다. 자본주의 사회에서는 인간이 살아가는 데 필요한 의, 식, 주 모두 돈으로 해결할 수 있다. 반대로 돈이 없으면 그 세 가지를 원활하게 공급받을 수 없다. 이 책의 저자는 그런 사실을 깨닫고 직장생활을 그만두었다. 쥐꼬리만한 월급을 받으면서, 그것도 원치 않는 일을 하면서 살아가는 그의 인생에 미래가 보이지 않았기 때문에 저자 주언규 씨(유튜버 신사임당)는 퇴사를 결심하고 사업을 시작한다. 오늘 소개하는 "킵고잉 : 나는 월 천만 원을 벌기로 결심했다"는 저자의 퇴사 ..