#기계진동
orthogonality와 eigen analysis에 관한 자세한 내용은 생략하고 어떤 식으로 다자유도계 비감쇄 진동 문제를 풀어나가는지 예제를 중심으로 알아봅시다.
Multi Degrre of Freedom System을 줄여 M-DOF 문제 라고도 하는데 M-DOF 문제에서 중요한 것은 modal matrix를 구하는 것입니다. modal matrix를 구한 후 이를 이용해 초깃값을 변환하고 변환된 해를 다시 역변환 하여 최종적인 해를 구성하는 것이 기본적인 흐름입니다.
이 글에서는 감쇄(Damping)가 없는 비감쇄 문제(Undamped System)만을 다루며 강제진동(Forced Vibration) 예제를 풀어보겠습니다.
1. 다자유도계 문제를 푸는 순서
다자유도계 문제를 푸는 순서는 다음과 같습니다.
1. 운동방정식으로부터 얻은 시스템의 특성방정식 -> 고유진동수(natural frequency) 구하기 -> 대응되는 모드 벡터(mode vector) 구하기
2. modal matrix 구하기
3. 초깃값 변환 : x(0) , x'(0) -> q(0) , q'(0)
4. 변환된 초깃값으로 q(t) 구하기
5. q(t)로부터 최종적인 해 x(t) 구성
2. 용어 설명
본격적인 예제 풀이에 앞서, 기호들과 각각에 대응되는 용어를 설명하겠습니다.
1.다자유도계의 일반적인 운동방정식 표현
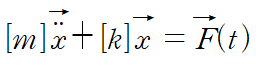
이런식으로 표현되는 연립 운동방정식을 위와 같이 행렬과 벡터로 한 번에 표현합니다.
예시로 아래와 같은 2자유도계 문제를 봅시다. 가운데 스프링 상수는 k2 = 2k라 하구요(n=2)
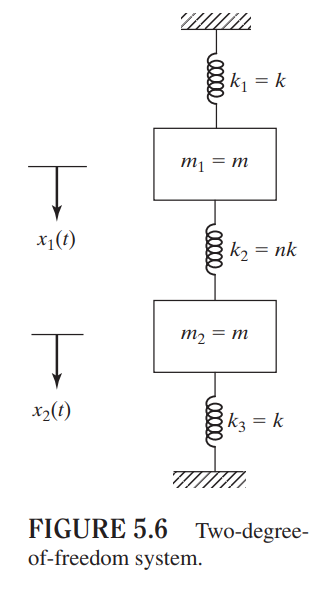
운동방정식은 다음과 같습니다

대괄호 표시는 행렬, 위에 화살표가 붙어있으면 벡터입니다.
이렇게 행렬과 벡터를 사용해 표현할 수도 있습니다.
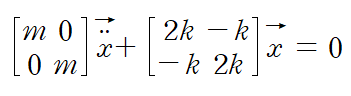
일반적으로 손으로 풀 수 있는 것은 운동방정식을 구성하는 행렬들이 symmetric, 즉 대각선 기준 대칭인 경우입니다.
만약 운동방정식을 구하고나서 봤는데 대칭이 아니라면(물론 그런 상황도 충분히 가능합니다) 계산 실수가 없었는지 확인해야 합니다.
다자유도계 문제는 이렇게 행렬 형태로 운동방정식을 정리하는 것부터 출발합니다.
2. 고유진동수
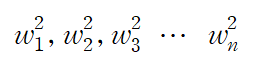
자유진동수라고도 불리는데 이 natural frequency는 질량-스프링으로 구성된 시스템의 고유한 특성입니다. 다시말해 특정한 질량과 스프링을 연결시켜놓으면 고유진동수가 정해진다는 것이죠
이 고유진동수는 해를 구성하는 중요한 요소입니다(삼각함수의 진동수가 됨)

위 행렬은 대각성분만 존재하고, i 행의 성분이 i 번째 고유진동수로 구성된 행렬입니다.
> 고유진동수 예시
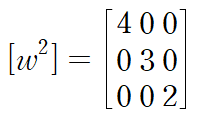
3. 초깃값의 표현
초깃값은 다음과 같이 벡터 형태로 표현합니다.
예시로 3자유도계의 초깃값을 가져왔으며, 자유도 만큼 초깃값이 주어져야 운동방정식의 해를 구할 수 있습니다.
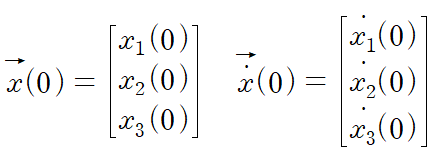
4. mode vector
고유진동수에 대응되는 벡터들로, 가능한 여러 진동의 형태를 의미합니다.
선형대수학의 고유벡터와 같은 방식으로 구합니다.
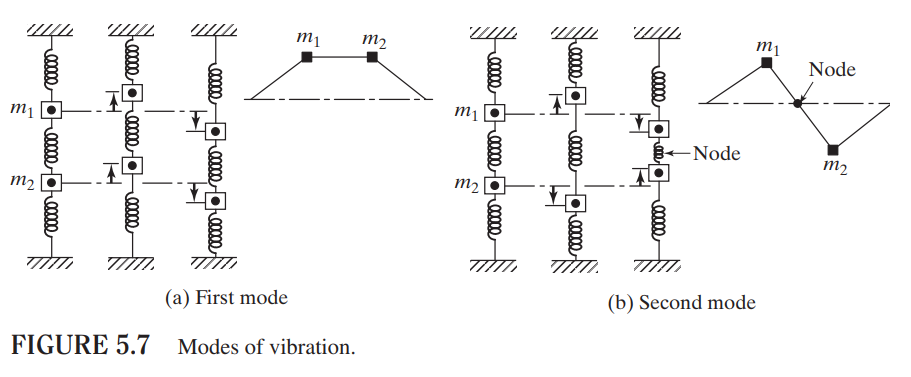
5. modal matrix [X]
mode vector들로 구성된 행렬입니다. 하지만 단순히 mode vector를 둔 게 아니라 특정 조건을 만족하도록 mode vector들의 크기를 조절하여 modal matrix를 구성해야 합니다.
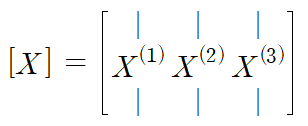
이렇게 구성한 modal matrix는 다음 두 가지 특수한 성질을 갖습니다.
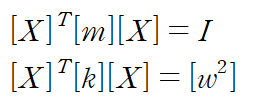
이것을 사용해 운동방정식을 정리하면 다음과 같습니다.
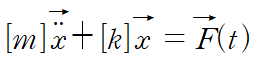
여기서 x(t) = [X]q(t)라는 변환을 사용합니다.
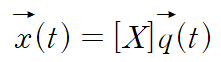
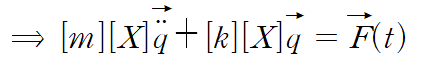
양변에 modal matrix의 transpose를 곱합니다(기존 행렬과 벡터의 왼쪽에)
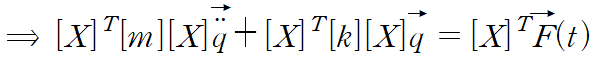
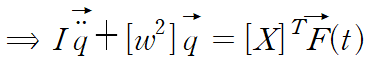
우변을 Q(t)라고 정의한다면
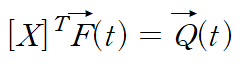
아래와 같이 깔끔하게 변환된 연립 미분방정식을 얻습니다.
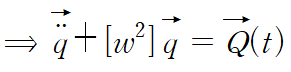
i번째 요소에 대한 미분방정식은 다음과 같습니다.
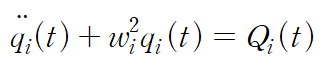
이 미분방정식의 해는 다음과 같습니다.
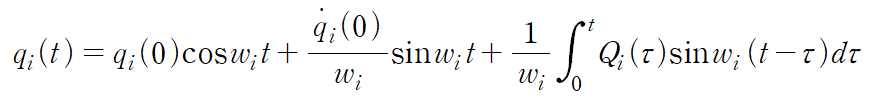
우변에서 첫 번째, 두 번째 항은 초깃값에 의해 결정되는 homogeneous solution이고 세 번째 항은 외력에 의한 particular solution입니다. 일반적인 외력을 고려해 convolution이 사용되었지만 주기함수나 단순한 외력이라면 일반적인 특수해 구하는 방식처럼 해를 구성하면 됩니다.
이제 이 q(t)를 다시 역변환 하면 x(t)를 구할 수 있습니다.
이따 예제로 설명하겠지만 간단히 처음 정의한 q(t) 정의식으로부터 구합니다.
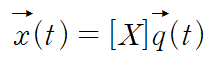
즉 modal matrix에 q(t)를 곱하는 것이 바로 역변환 과정이 됩니다.
3. 예제 : 강제진동(Forced vibration) 문제
(예제) Determine the amplitude of motion of the three masses in figure
with m = 1kg, k = 1000 N/m, F(t) = 5sin10t N
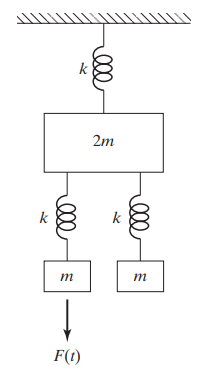
외력이 삼각함수로 주어졌을 때의 steady state response를 구하라는 문제입니다.
다자유도 문제를 푸는 순서를 다시 되짚어보겠습니다.
1. 운동방정식으로부터 얻은 시스템의 특성방정식 -> 고유진동수(natural frequency) 구하기 -> 대응되는 모드 벡터(mode vector) 구하기
2. modal matrix 구하기
3. 초깃값 변환 : x(0) , x'(0) -> q(0) , q'(0)
4. 변환된 초깃값으로 q(t) 구하기
5. q(t)로부터 최종적인 해 x(t) 구성
1. 시스템의 운동방정식은 다음과 같습니다.
위에서부터 질량 m1, m2, m3라 잡고 각각의 변위를 x1, x2, x3이라 잡은 겁니다.
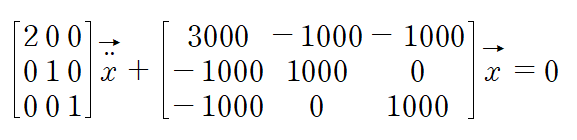
특성방정식은 다음과 같습니다.
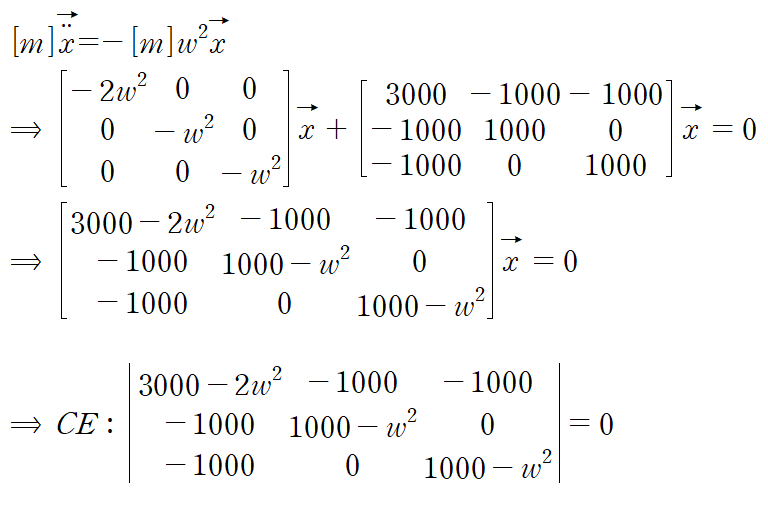
위 행렬식을 풀어서 얻는 w는 다음과 같습니다.
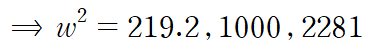
고유진동수를 구했으니 이제 각 고유진동수에 해당하는 모드벡터를 구해주면 됩니다.
각각의 고유진동수를 대입해도 되고 일반화시킨 다음 w를 대입해 구해도 됩니다.
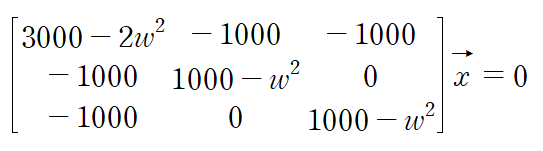
가장 간단한 행부터 정리합니다.
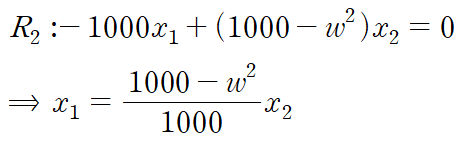
x2에 대하여 정리해봅시다.

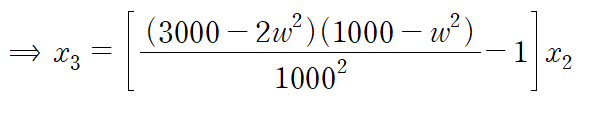
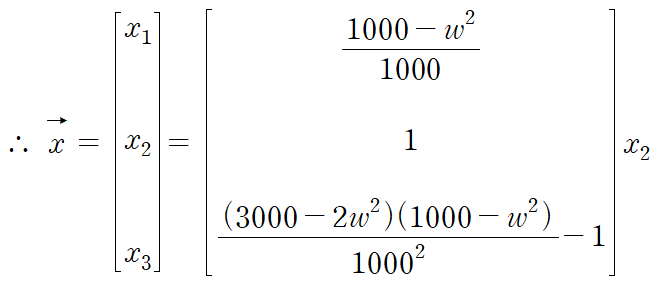
이것에 고유진동수를 넣으면 모드벡터들을 구할 수 있습니다.
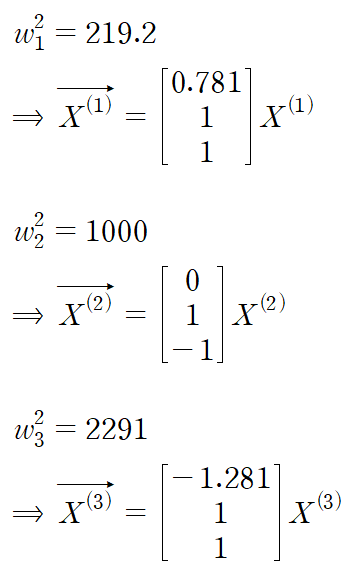
모드벡터들의 위첨자를 "슈퍼"라 읽습니다.
X(1)을 "X 슈퍼 원", X(2)를 "X 슈퍼 투" 이렇게 말입니다.
2. modal matrix
앞서 얻은 모드벡터들로 modal matrix를 구성합니다.
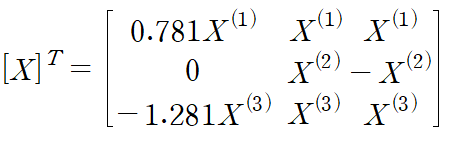
이것이 아래 조건을 만족시키도록 X1, X2, X3 을 구합니다.
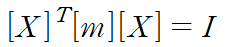
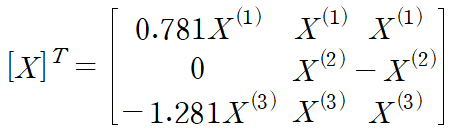
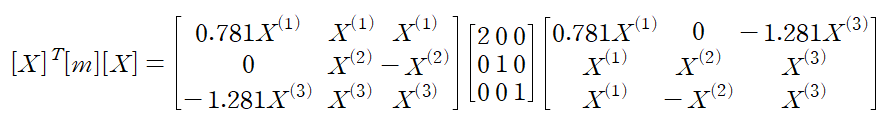
행렬계산을 거치면 다음과 같은 결과를 얻습니다.

1이 되야 한다는 조건은 우변이 단위행렬이라는 것에서 왔습니다.
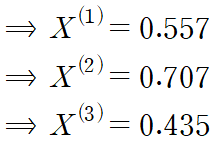
따라서 modal matrix는 다음과 같습니다.
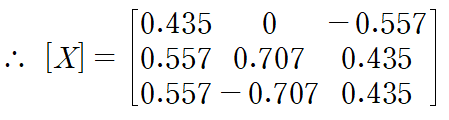
이것을 쉽게 구할 수 있는 공식이 있습니다.
만약 mass matrix [m]이 대각성분만 존재한다면 다음과 같은 공식을 통해 mode vector들의 크기를 구하고 빠르게 modal matrix를 구할 수 있습니다.
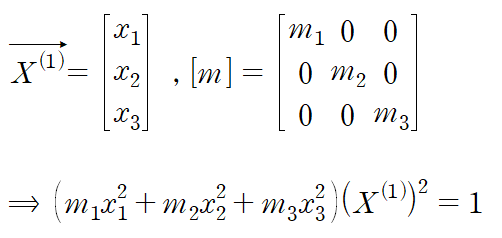
※ 이것은 [m]이 대각행렬일 때만 적용가능합니다. 이중, 삼중 진자운동의 경우 mass matrix가 대각행렬이 아닙니다.
또한 기존 정의식에 대입해 modal matrix를 잘 구했는지 확인합니다.
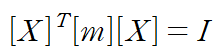
3. 초깃값을 사용하는 것은 homogeneous solution에 해당하는 것이므로, 이 예제에서는 해당되지 않습니다.
4. 이제 고유진동수를 가지고 q(t)를 구해봅시다.
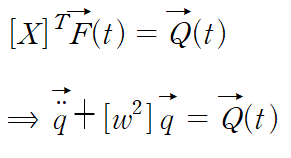
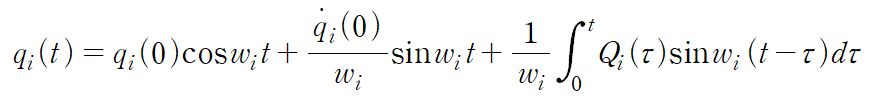
위 식은 general solution을의미하고 이 문제에서는 초깃값이 고려되지 않으므로(steady state response;particular solution) q(0)와 q'(0)이 모두 0이고 특수해만을 구해주면 됩니다. 위 식에는 일반적인 외력을 생각해서 합성곱(convolution)으로 표현되었지만 일반적인 특수해 구하는 방법을 사용해도 됩니다.
이 문제에서는 미정계수법을 사용하겠습니다.
가장 먼저 해야 할 일은 외력F(t)를 Q(t)로 바꾸는 일입니다.
F(t)는 왼쪽 아래에 있는 1kg 질량에 부착되어있습니다. 이것을 두 번째 질량 성분이라고 잡겠습니다.(이미 그렇게 두고 풀어온 것..)
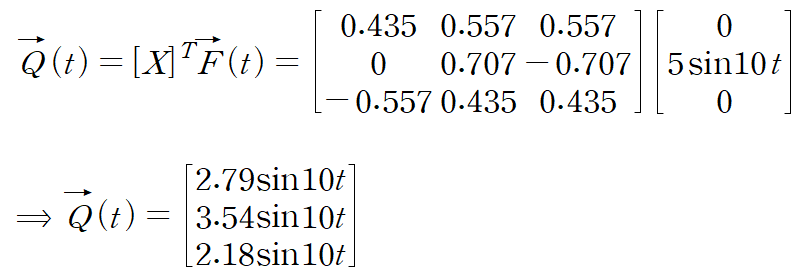
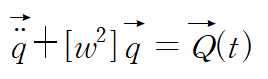

앞서 구한 고유진동수를 사용합니다.
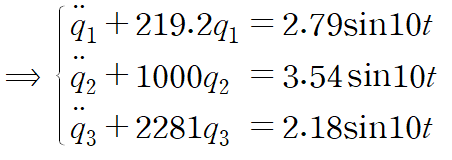
특수해를 구합니다.
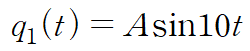
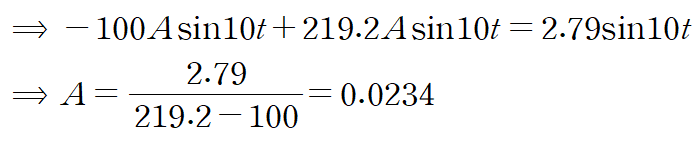
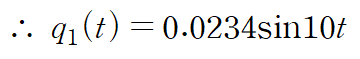
이와 같은 방법을 사용해 q2, q3도 구합니다.
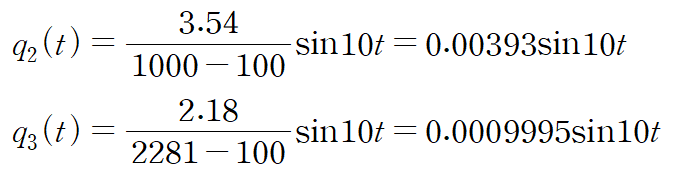
전체해를 작성합니다.
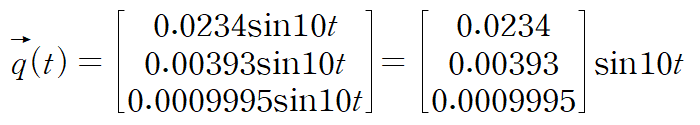
5. 이제 마지막으로 mordal matrix와 q(t)를 사용해 최종해 x(t)를 구합니다.
앞서 정의한 변환식을 그대로 사용합니다.
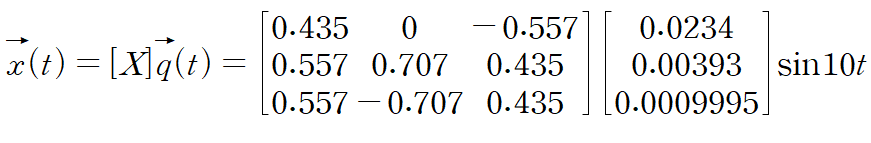
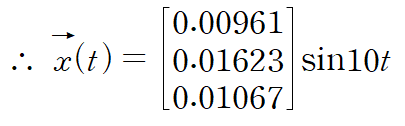
아래와 같이 표현할 수도 있습니다.
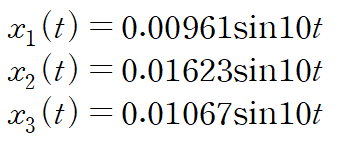
※ 질량체들의 순서를 바꿔서 계산하면 mordal matrix와 Q(t)등 문제 중간 과정은 다를 수 있으나 최종적인 결과는 같습니다.
'기계공학 > 기계진동' 카테고리의 다른 글
| [기계진동] 1차원 강제진동 - 감쇄모델 (0) | 2024.03.29 |
|---|---|
| [기계진동] 1차원 강제진동 - 비감쇄모델 (1) | 2024.03.28 |
| [기계진동] 1차원 자유진동 - 감쇄모델 (0) | 2024.03.27 |