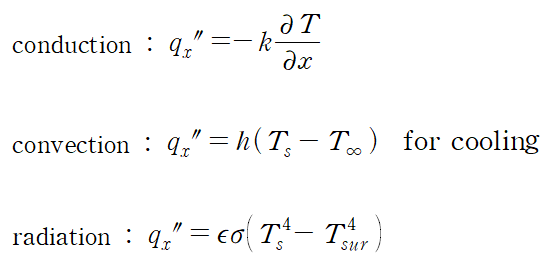#열전달 유체역학에서 주요 관심사가 압력분포와 속도분포이듯 열전달에서의 주요 관심사는 온도분포(temperature distribution)와 열전달량(heat)입니다. 온도분포를 알게 되면 heat flux와 heat rate를 알 수 있기 때문인데 세 가지 열전달 모드(전도, 대류, 복사)에 대한 heat은 모두 temperature 로 기술되어 있습니다. 때문에 열전달에서 물어보는 것이 대부분 이 온도와 열전달량(heat flux, heat rate)에 초점이 맞춰질 수밖에 없습니다. 이런 이유로 우리도 문제를 대할 때 온도분포와 열전달량에 관심을 가지는 것이 자연스러운 수순입니다. 간단한 예제들로 전도 열전달, 온도분포, 열전달량에 익숙해져봅시다. Examp..