#수치해석
Runge-Kutta Method
룽게 쿠타 방법은 초깃값 문제, 즉 아래와 같은 미분방정식을 푸는 수치해석 기법이다.

아래와 같은 미분방정식을 룽게 쿠타 방법으로 풀 수 있다.


오일러 방법(Euler's method), 호인의 방법(Heun's method), 중간점 방법(Midpoint method) 등의 미분방정식을 푸는 여러 가지 기법은 대부분 이 룽게-쿠타 방법의 일종이다.
RK method는 선형 미분방정식이 아니라 비선형 미분방정식에도 적용할 수 있다는 매우 큰 장점이 있다.
다음과 같은 방법을 Runge-Kutta Method라고 한다.

여기서 h는 step size이고

φ(phi) 는 함숫값들로부터 계산되는 어떤 값이다.
원하는 만큼 k_n을 설정할 수 있으며 가장 간단히, 상수로 φ를 설정한다면 다음과 같이 해당 점에서의 접선의 기울기를 사용할 수도 있겠다.

방법 자체는 간단한데 이 φ를 어떻게 설정하느냐에 따라 정확도가 달라지는 것이다.

이때 a,k,p,q는 다음과 같은 의미를 가진다.

즉 현재 y값(y_i)을 reference로 여러 함숫값들을 종합해서 그 다음 y값(y_i+1)을 추정할 수 있다는 것이다.
복잡해보이지만 일반적으로 k4까지만을 사용한다.(4차 RK method)
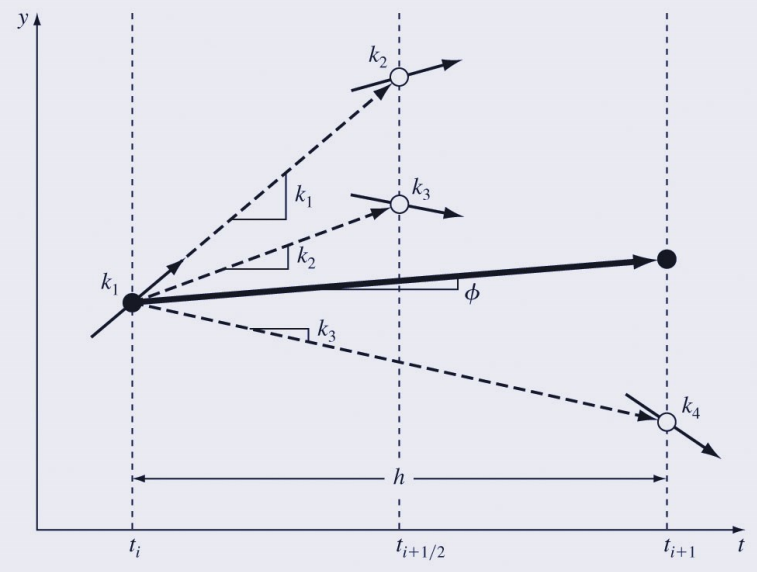
룽게 쿠타 4차 방법은 다음과 같이 k1, k2, k3, k4를 사용한다.

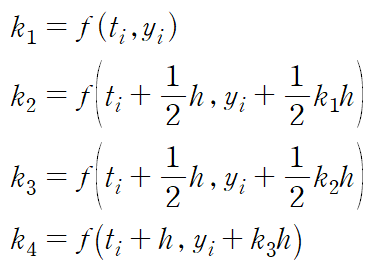
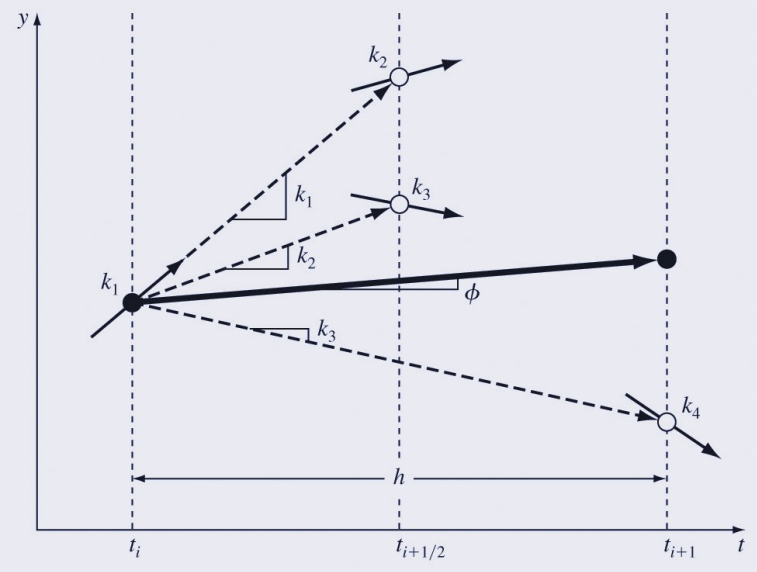
아래 그림과 같이 현재 지점에서 4개의 함숫값을 가지고 다음 지점을 예측하는 것이 4차 룽게 쿠타 방법이다.
각각의 계수와 상수 p, q는 테일러 급수전개로부터 구할 수 있으며 뒤에서 2차 RK method의 계수들을 유도해볼 것이다.
통상 n이 늘어날 수록 정교해지며 오일러 방법은 1차 RK method에 속하고 호인의 방법, 중간점 방법은 모두 2차 RK method에 속한다.
실용성이 높은 4차 RK method는 손으로 풀기에는 계산량이 많아 느리지만 그만큼 상당히 작은 오차를 얻는 매우 매우 매우 강력한 방법이다.
위에서 테일러 급수전개를 언급했는데 Runge-Kutta method는 "테일러 급수의 정확도를 고차 미분항 계산없이도 끌어올릴 수 있다"는 의미를 가지고 있다. 테일러 급수의 정확도는 expansion된 중심으로부터 얼마나 떨어져있냐, 고차 미분항이 어디까지 포함되느냐에 따라 결정되는데 RK method는 그것을 여러 지점의 함숫값으로 대체하는 것과 같은 것이다.
Derivation of 2nd order RK method
복잡해보이는 룽게 쿠타 방법의 정의식을 이해하기 위해 2차 RK method를 유도해보자
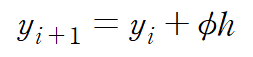
2차 RK method는 φ을 다음과 같이 2번째 항까지만 가져간다는 것이다
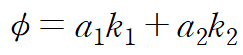
따라서 2차 RK method는 다음과 같이 정리된다
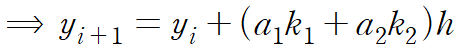
앞선 정의에 의해 k1, k2는 다음과 같다
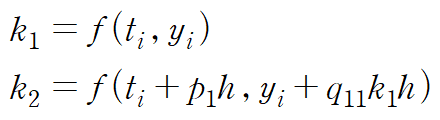
즉 a1, a2, k1, k2를 정해야 하는데 k1는 현재 지점의 함숫값으로 정해져있고
k2를 정하기 위해 p1, q11을 정해야 한다.
이 상수들은 테일러급수로부터 결정할 수 있다.
2차 테일러 급수 식은 다음과 같다.
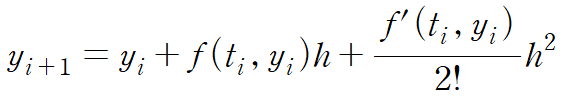
이때 f의 도함수는 t에 대해 미분한 도함수이며 연쇄법칙에 의해 다음과 같이 표현된다.
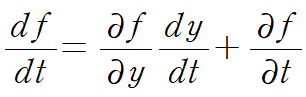
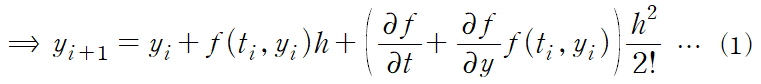
이때 dy/dt = f(t,y)이므로
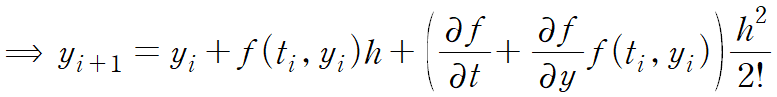
여기서 k2를 이변수함수로 취급하고 우변에 대해 테일러 급수를 전개한다.

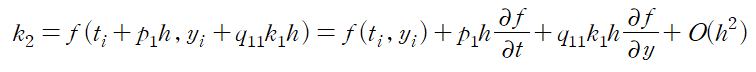
마지막 O(h^2)는 오차항이다.(error)
위 식의 양변에 a2h를 곱하자
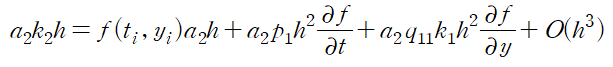
처음 정의한 2차 RK method에 이것을 대입하고 정리한다.
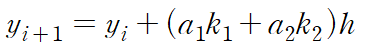
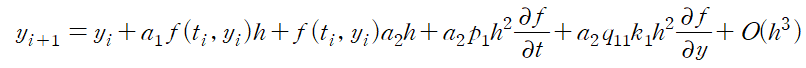
k1 = f(t_i , y_i )를 적용하고 h에 대해 오름차순으로 정리한다.
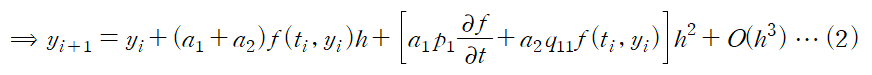
이제 위 (2) 식과 (1) 식의 양변을 비교하면 아래와 같이 계수 a1, a2, p1, q11를 결정하는 세 조건을 얻을 수 있다.
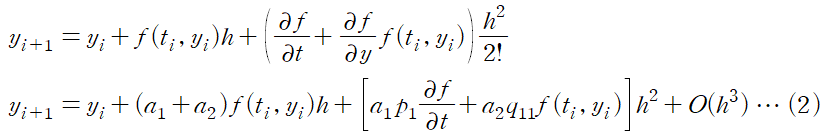
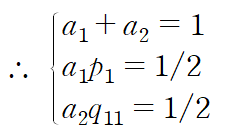
2차 RK method의 일종인 호인의 방법은 a1 = a2 = 1/2 로 설정한 것이다.
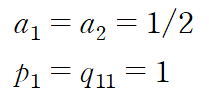
오차항은 h의 세제곱의 함수이므로 간격이 좁아질 수록 그 오차가 매우 작아진다는 것을 예상할 수 있다.
Example
룽게 쿠타 4차 방법, 또는 4차 룽게 쿠타 방법은 다음과 같다.
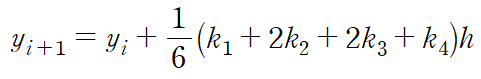
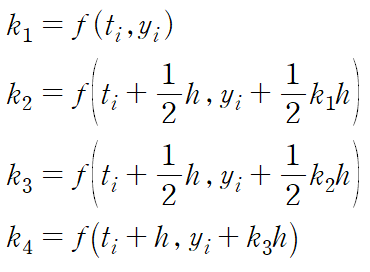
(예제) 주어진 미분 방정식에 대해 y(1)을 구하여라. 이때 step size는 0.25로 한다.
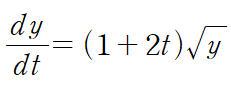
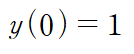
step size가 0.25, 즉 h = 0.25라는 것은 문제에서 원하는 y(1)를 구하기 위해 y(0.25), y(0.5), y(0.75)를 거쳐야 한다는 뜻이다.
> 풀이

'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 다항회귀 예제(Polynomial Regression), 매트랩 코드 (0) | 2023.07.29 |
|---|---|
| [수치해석] 비선형 회귀(Nonlinear Regression) 예제, 매트랩 코드 (0) | 2023.07.27 |
| [수치해석학] LU분해(LU Factorization), 파이썬 코드 (1) | 2023.01.26 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |
| [수치해석학] 뉴턴 보간법 (Newton's Interpolating Polynomial, Divided difference) (0) | 2021.12.16 |