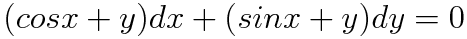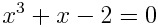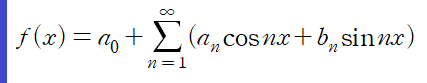SUBORATORY

1. 코시-리만 방정식 (Cauchy-Riemann Equations) ​ z = x + yi 인 복소공간에서 f(z) = u(x,y) + i v(x,y) 가 연속이고 미분가능하면 u, v는 아래 방정식을 만족합니다. ​ ​ 위 방정식을 코시-리만 방정식이라 부릅니다. ​ 즉 f(z)가 정의역 D에서 해석적(analytic)이라면 D의 모든 점에서 f(z)의 편도함수가 존재하고 코시-리만방정식을 만족합니다. ​ ​ 2. 증명 ​ 복소함수는 어느 방향으로 Δz 를 잡더라도 미분계수가 존재할 때 미분가능합니다. ​ 따라서 x, y 두 방향으로의 f(z) 미분계수를 따져봅시다. ​ ​ Δx와 Δy를 이용해 f'(z)를 표현합니다. ​ 이때 1번 경로는 Δy=0 인 경우니까 1번 경로에 대한 임의의 점 z에서의..

미분의 역연산이 되는 적분으로 이루어진 적분방정식을 알아봅시다. 더불어 라플라스 변환을 이용해 적분방정식의 해를 구해봅시다 ​ ​ (i) Definition 적분방정식의 형태 ​ ​ ​ 위 두 방정식처럼 해가 되는 함수인 y(t)의 적분형태가 포함된 방정식을 적분방정식이라고 합니다. 첫 번째 방정식의 경우 양변을 미분해서 해를 구하는 일반적인 미분방정식의 해를 구하듯 y(t)를 구할 수 있습니다. 그러나 두 번째 방정식의 경우 그게 불가능합니다. t로 미분을 해야 하는데 피적분함수 내에 t가 포함되어 있기 때문이죠. 이정도는 고등학교 미적분에서 다 배우는 상식.수준입니다. 아무튼 적분방정식의 형태는 위와 같습니다. ​ ​ ​ (ii) Application ​ 합성곱에 라플라스 변환을 취하면 아래와 같은 ..

#공업수학 Convolution으로 번역되는 합성곱에 대해서 알아봅시다. ​ ​ (i) Definition 합성곱의 정의 ​ 두 함수 f와 g에 대해 합성곱은 자를 사용해 표현하고, 아래와 같이 적분식으로 정의됩니다. ​ ​ 직관적으로 찾아내신 분도 계시겠지만, 합성곱은 교환법칙이 성립합니다. ​ 위 합성곱의 정의식에서 라고 u를 설정합니다. u로 설정함과 동시에 적분구간과 문자에 변화가 생깁니다. ​ ​ u와 t를 이용해 다시 정리하면 ​ ​ 합성곱 정의식의 τ(tau)가 u로 바뀐 것 빼고는 달라진 게 없죠? 즉 u를 다시 τ를 사용해서 표현해도 무방합니다. ​ ​ 이상의 결과를 정리하면 교환법칙이 성립함을 알 수 있습니다. ​ ​ ​ (ii) Application ​ 합성곱에 라플라스 변환을 취하면..

​ Dirac delta function. 6.4는 디랙 델타 함수에 대한 내용입니다. 먼저 디랙 델타 함수의 정의를 봅시다 ​ (i) Definition ​ t=a라는 임의의 점에서 함숫값이 매우 큰 함수를 디랙 델타 함수라고 합니다. 짧은 시간 안에 강한 임펄스가 가해진다는 뜻에서 Short Impluse 라고도 합니다. unit step function과 유사하게 unit impulse function 라는 이름도 가지고 있습니다. ​ 디랙 델타 함수는 여러 근사 표현을 가지고 있는데, 공업수학에서는 그중 가장 간단한 표현을 사용합니다 ​ 위와 같이 fk(t-a)를 설정한 후 극한을 취해 디랙 델타 함수를 표현할 수 있습니다. ​ ​ k의 값에 관계 없이 fk(t-a)와 t축이 이루는 면적은 항상 ..

이전에 포스팅한 라플라스 변환은 f(t)에 관한, 즉 일변수 t에 대한 상미분방정식을 풀기 위한 해법으로써 소개되었다. 대수방정식을 거쳐 해를 구한다는 다소 편리한 이 라플라스 변환은 상미분방정식을 넘어 편미분방정식에도 적용될 수 있다(!). ​ ​ 편미분방정식을 라플라스 변환으로 풀기 위해서는 몇가지 기본전제(지식)가 필요하다. ​ 1. 본 포스팅에서 다뤄지는 함수 w는 모두 이변수 함수 w(x,t)이다. 2. 라플라스 변환 시 적분은 한 문자에 대해서만 수행된다. 3. 역변환 또한 한 문자에 대해서만 수행된다. 4. W(x,s)는 함수 w(x,t)에 라플라스 변환을 수행한 함수이다. ​ 편미분방정식에서 주의해야 할 것은 변수의 혼동이다. 라플라스 변환을 수행할 때 x와 t가 아무 관계 없는 독립변수이..

완전미분방정식이 무엇인지, 어떻게 판별하는지, 어떻게 푸는지에 대해서는 아래 링크를 참조바랍니다. 풀이과정이 다소 길고 복잡하기 때문에 예제 파트를 따로 나누었습니다. 이번 포스팅에서는 네 개의 미분방정식 예제를 소개하는데, 이를 통해 완전미분방정식에 대한 감이 잡히길 바랍니다..! blog.naver.com/subprofessor/222094820066 (예제 1) 다음 미분방정식의 완전성을 검사하여라 dx앞에 있는 놈들을 y에 대해 편미분해주고, dy앞에 있는 놈들을 x에 대해 편미분해줍니다. 음! 뭔가 둘이 안맞네 하죠? 맞아요 완전미분방정식이 아닙니다. 이런 간단한 문제가 시험에 나올 일은 없지만 만약 나온다면 저는 이렇게 답안을 작성할 것 같네요 해당 미분방정식에 대해 완전성 검사를 시행한 결과..

오늘은 Erwin Kreyszig 의 Advanced Engineering Mathematics 에 수록된 선적분 예제를 풀어보자 ​ PART 1) 일반적인 선적분 계산 를 구하여라 ​ ​ (예제 1) ​ ​ ​ ​ (예제 2) ​ ​ ​ ​ ​ ​ (예제 3) ​ 곡선 C는 위와 같다 ​ ​ ​ ​ PART 2) C가 폐곡선인 경우 를 구하여라 ​ (예제 1) ​ ​ 경로를 매개변수 t 로 나타내면 아래와 같다 ​ 곡선 C가 폐곡선이므로 선적분은 폐곡선에 대한 선적분이다 ​ 사실 그린정리나 스토크스 정리 등이 아니라 일반적인 선적분 계산 문제에서는 폐곡선이냐 아니냐가 딱히 중요하지 않습니다. 생긴것만 저렇게 생겼지 동일한 방법으로 계산합니다 ​ ​ ​ ​ PART 3) F가 경로 독립(Path Inde..

사실 공업수학에서 미분방정식의 해를 구하기 위해 사용하는 방법이지만 별도로 미분적분학에 먼저 포스팅한다. ​ 라플라스 변환은 미분방정식을 대수방정식 꼴로 변환시켜 보다 쉬운 방정식을 풀 수 있다는 이점을 가지고 있는 변환법이다. ​ 대수방정식은 이런 애들을 칭하는 말이다. 대수적인 특성을 가지고 있는 방정식을 의미하며(당연히..) 사칙연산을 통해 해를 구할 수 있는 방정식을 의미한다. 미분방정식은 미분개념과 적분개념이 모두 포함되어 있는 방정식인데, 이 방정식은 애초에 사람이 인지하기가 어렵다. 변화율을 인지하는 것 자체가 어렵기도 하고 지수함수나 삼각함수와 같은 초월함수들이 포함될 경우 더더욱 이해하기가 어렵다. 반면 대수방정식은 인수분해 또는 근의 공식을 통해 쉽게 해를 구할 수 있다는 장점이 있다...

푸리에 급수란? 푸리에 급수(Fourier Series) 는 삼각함수들의 합으로 주기함수를 나타내는 방법이다. 나중에 푸리에 적분에서는 주기함수라는 조건이 무의미해지는 지경까지 이른다.(주기를 무한대로 잡은 것..) "대체 이걸 어떻게 떠올린 거지?"라는 생각이 안 날 수가 없는 위대한 발견이다. 푸리에 급수는 파동분석을 하기 위한 기초 개념이다. 푸리에 변환은 주기함수건, 비주기함수건 상관없이 삼각함수의 합 꼴로 함수를 해석할 수 있게 도와주는 도구다. 파일 압축에도 사용된다는데 거기까지는 아직 내 분야가 아니라 Pass.. 우리의 목표는 푸리에 변환까지다. 아무튼 이 "푸리에 XX"를 통틀어 푸리에 분석(Fourier Analysis)이라고 부른다. 아무튼 그 푸리에 분석의 기초가 되는 '푸리에 급수..

미분방정식이란 말은 왠지 모르게 멋있다. 고등학교 들어와서 '미분방정식'푸는 공대 형들이 참 멋있어보였다. 나만 그런가..? 아무튼, 실제로 미분방정식은 "멋있다." 자동차를 굴리는 힘인 엔진에서도 미분방정식을 빼놓고 설명할 수 없으며 바짓주머니 속에 있는 스마트폰에서도, 릴라드가 던진 클러치 3점슛에서도 미분방정식은 등장한다. 공업수학을 배우고 나면 사회 전반에 미분방정식이 관여하고 있음을 깨닫는다. 도대체 미분방정식이란 게 뭘까? (i) 미분방정식? 미분방정식이라는 건 [미분]+[방정식] 같은 느낌으로 이해하면 된다. 고등학교 때 배우는 미적분과 초등학교 때 배우기 시작하는 방정식의 '역대급' 콜라보랄까? 한창 과외를 할 때 방정식의 정의를 모르는 학생들을 참 많이 만났다. 방정식의 정의는 다음과 같..