푸리에 급수란? |
푸리에 급수(Fourier Series) 는 삼각함수들의 합으로 주기함수를 나타내는 방법이다. 나중에 푸리에 적분에서는 주기함수라는 조건이 무의미해지는 지경까지 이른다.(주기를 무한대로 잡은 것..) "대체 이걸 어떻게 떠올린 거지?"라는 생각이 안 날 수가 없는 위대한 발견이다.
푸리에 급수는 파동분석을 하기 위한 기초 개념이다. 푸리에 변환은 주기함수건, 비주기함수건 상관없이 삼각함수의 합 꼴로 함수를 해석할 수 있게 도와주는 도구다. 파일 압축에도 사용된다는데 거기까지는 아직 내 분야가 아니라 Pass.. 우리의 목표는 푸리에 변환까지다. 아무튼 이 "푸리에 XX"를 통틀어 푸리에 분석(Fourier Analysis)이라고 부른다. 아무튼 그 푸리에 분석의 기초가 되는 '푸리에 급수'를 알아보자
먼저 주기가 2π인 함수의 푸리에 급수전개를 보자

이때 삼각함수의 계수 an 과 bn 은 아래와 같이 정의된다. 왜 그런지는 다음 시간에 나올 증명 파트에서 살펴보도록 하고..
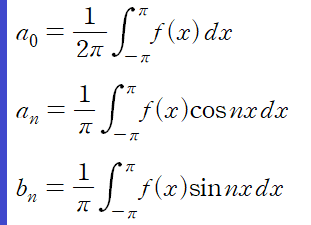
(예제 1)
주어진 f(x)를 푸리에 급수로 나타내어라

푸리에 급수의 정의에 따라 삼각함수의 계수(an과 bn)를 구해주면 된다.
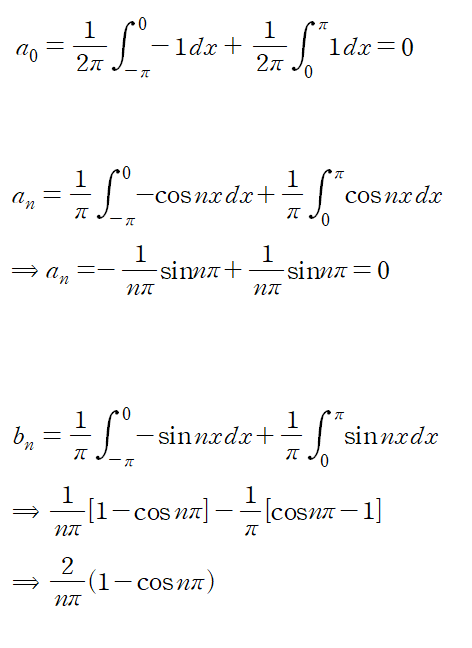
bn을 간단히 정리하면 아래와 같다.
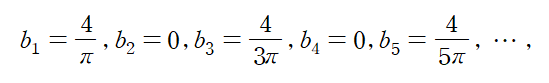
f(x)는 푸리에 급수의 정의에 의해
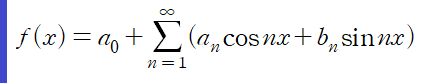
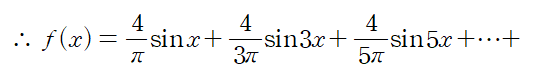
이다.
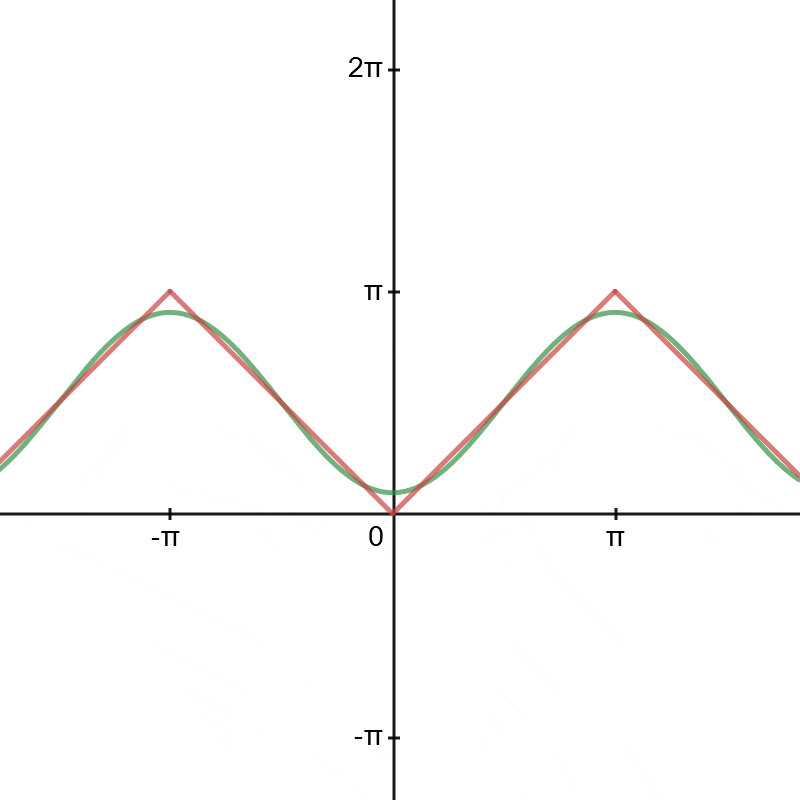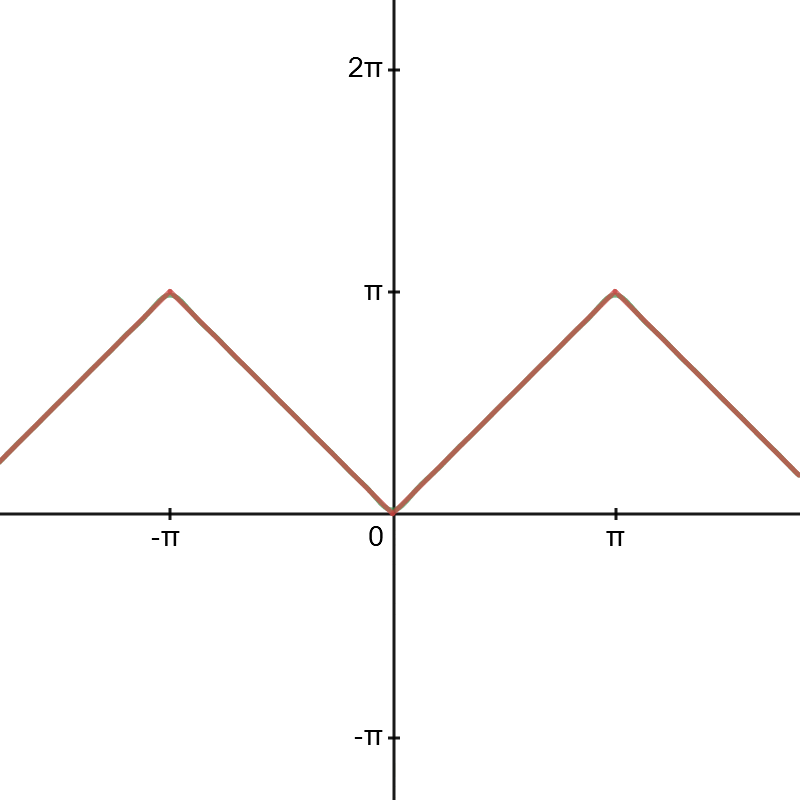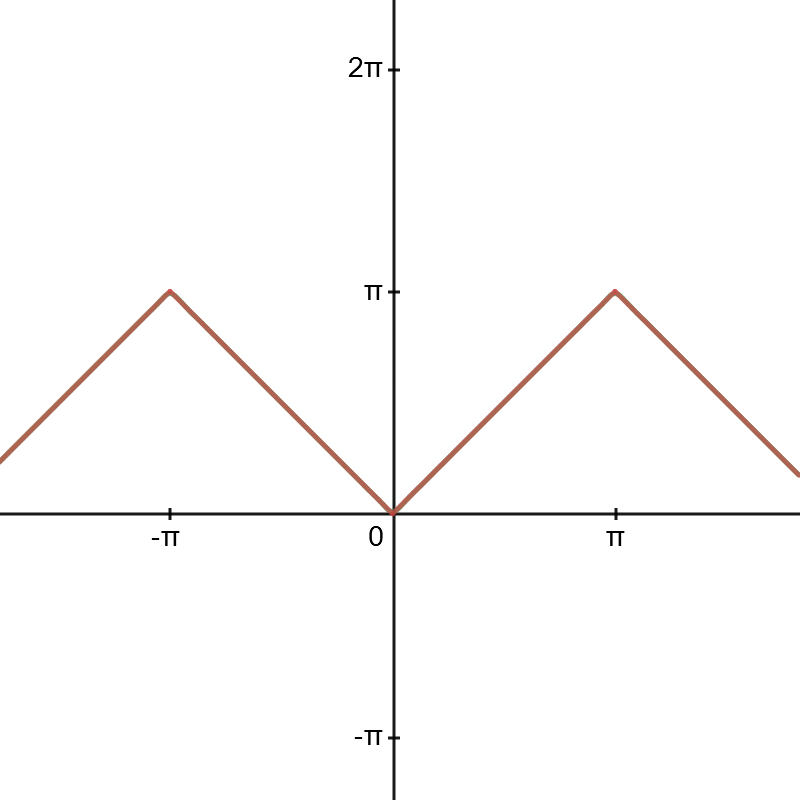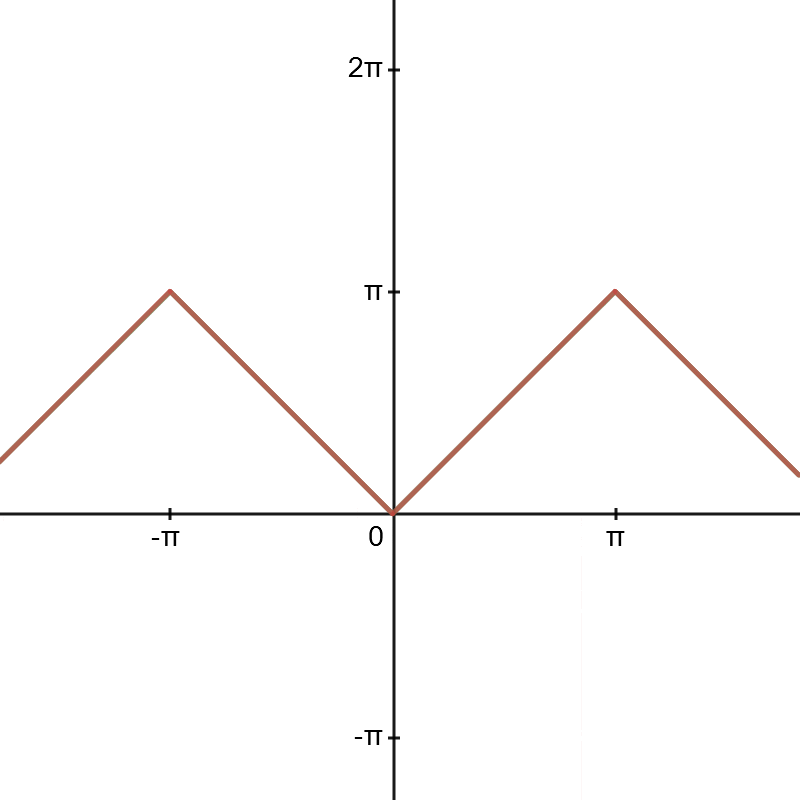
구한 삼각함수의 합들이 정말로 원래 주어진 f(x)와 동일한가?에 대해서는 그래프를 통해 직접 알아보자
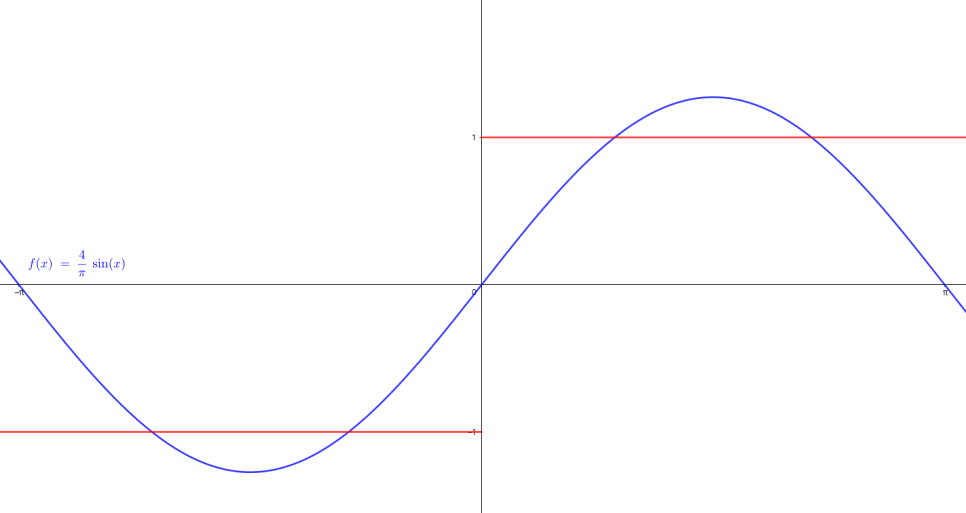
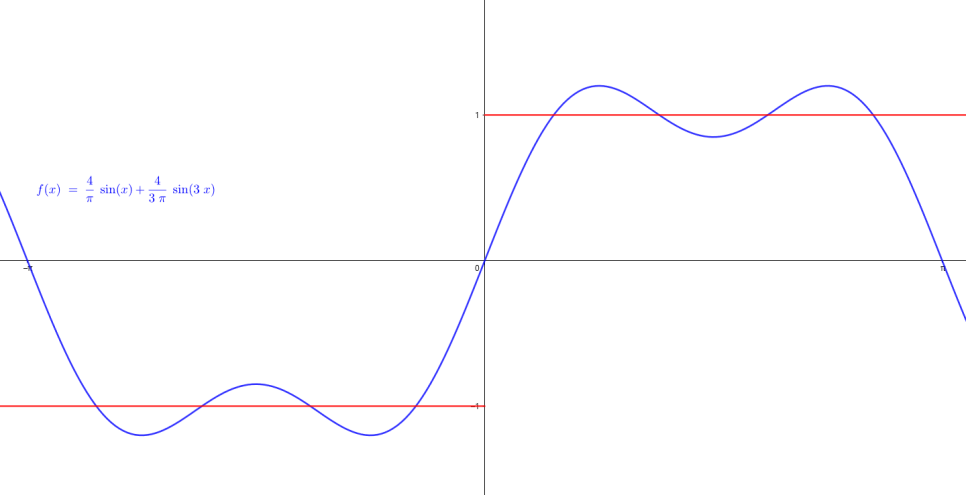

항이 하나씩 늘어갈 때마다 근사화되는 f(x)의 모습을 볼 수 있다



항이 늘어갈 수록 원래 함수와 많이 비슷해진다
(예제 2)
주어진 f(x)를 푸리에 급수로 나타내어라

마찬가지로 정의에 따른 삼각함수의 계수를 구하자
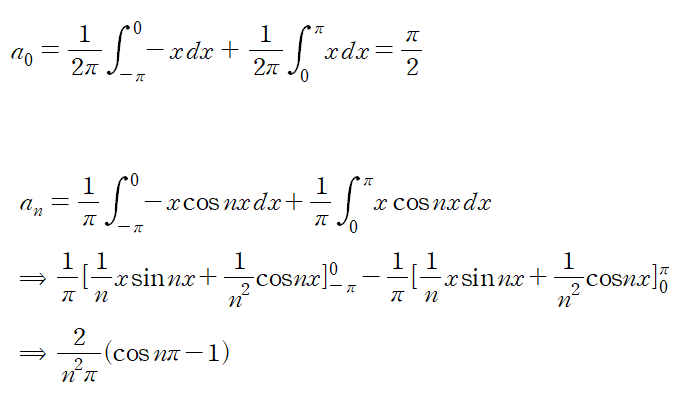
n에 따른 an을 간단히 나타내보면 아래와 같다

다음은 bn.

bn=0임은 직접 정적분의 값을 구하는 방법도 좋지만 피적분함수가 기함수이므로 0임을 보이는 풀이도 좋다
따라서 f(x)를 푸리에 급수로 표현하면 아래와 같다

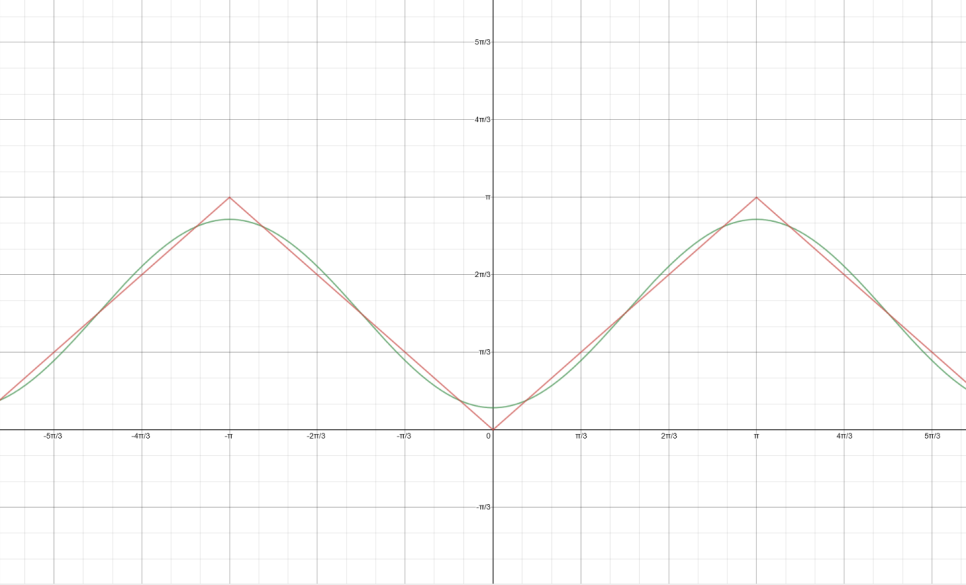
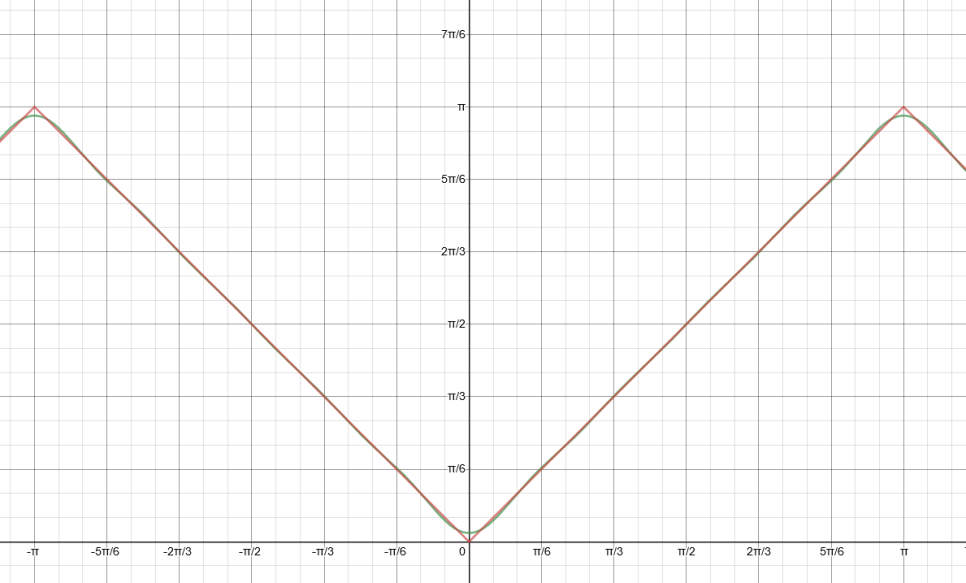
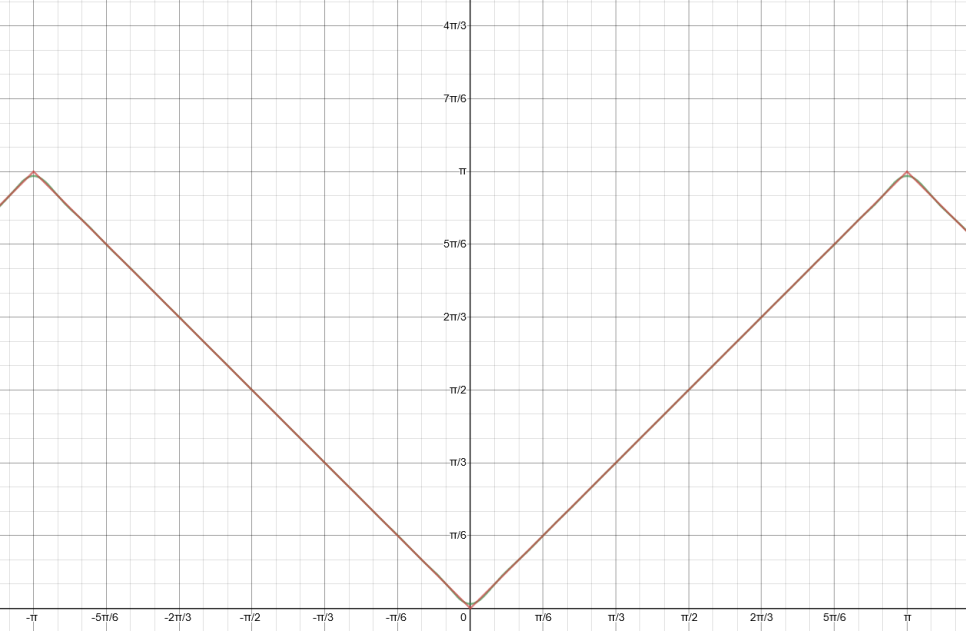
진짜 위 삼각함수의 합이 원래 f(x)의 그래프와 얼마나 같은지 항을 하나씩 늘려가며 그래프를 살펴보자

(예제 3)
주어진 f(x)를 푸리에 급수로 나타내어라

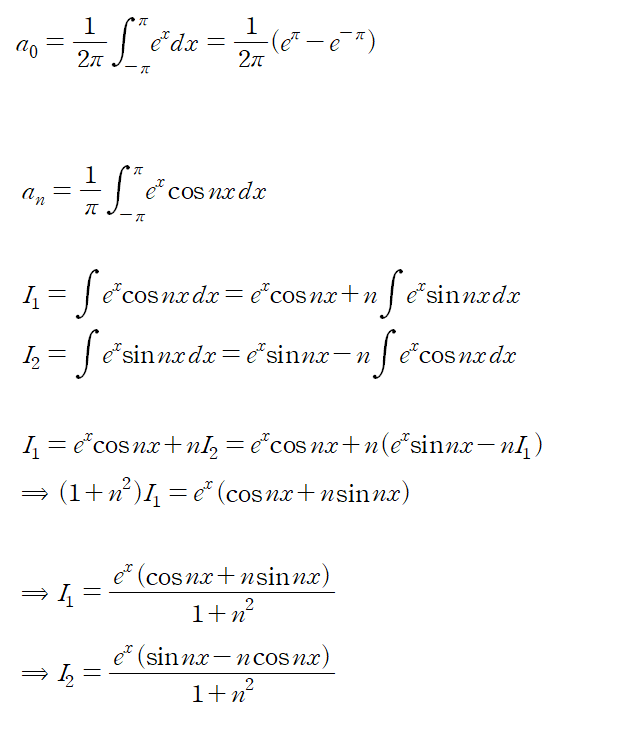
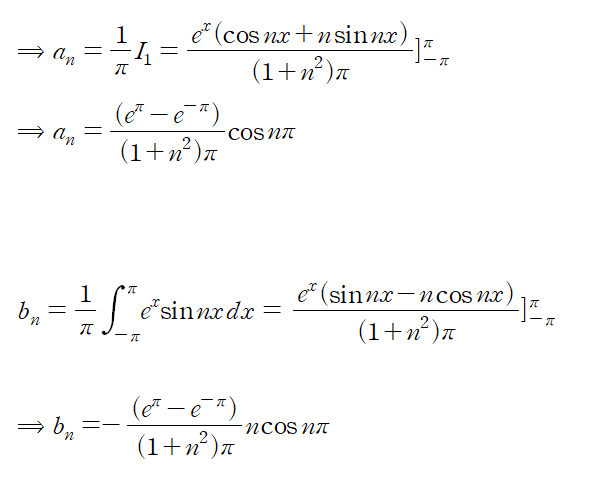
편의상 I1와 I2라고 두 적분을 정의해 an과 bn을 구하였다
푸리에 급수의 정의에 의해 f(x)는 다음과 같다
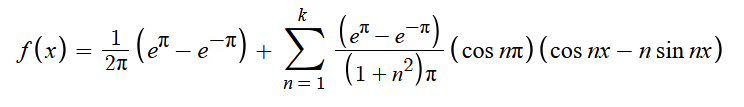
이번에도 그래프를 통해 검증해보자
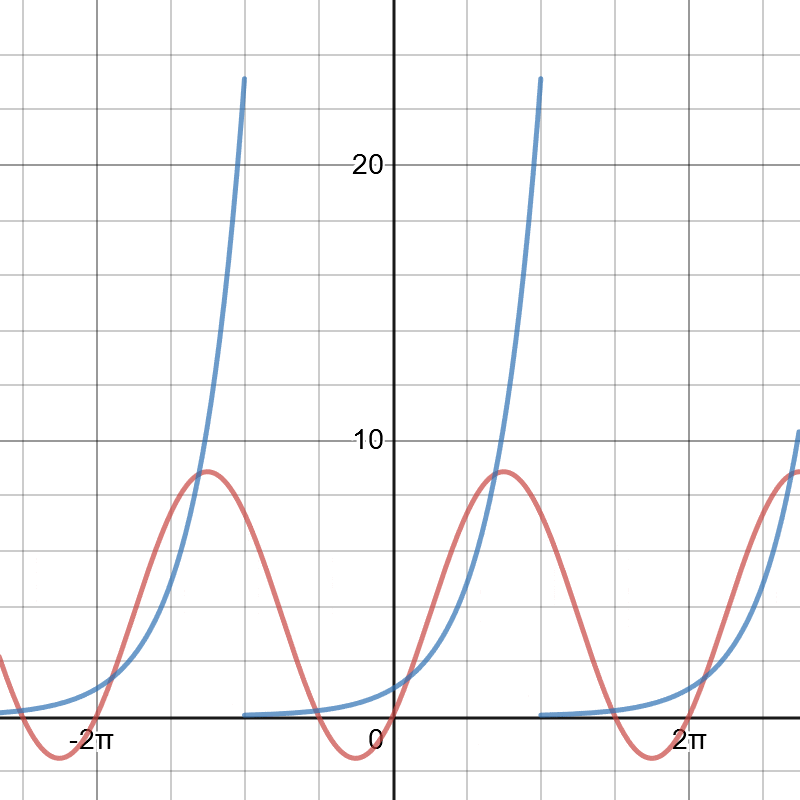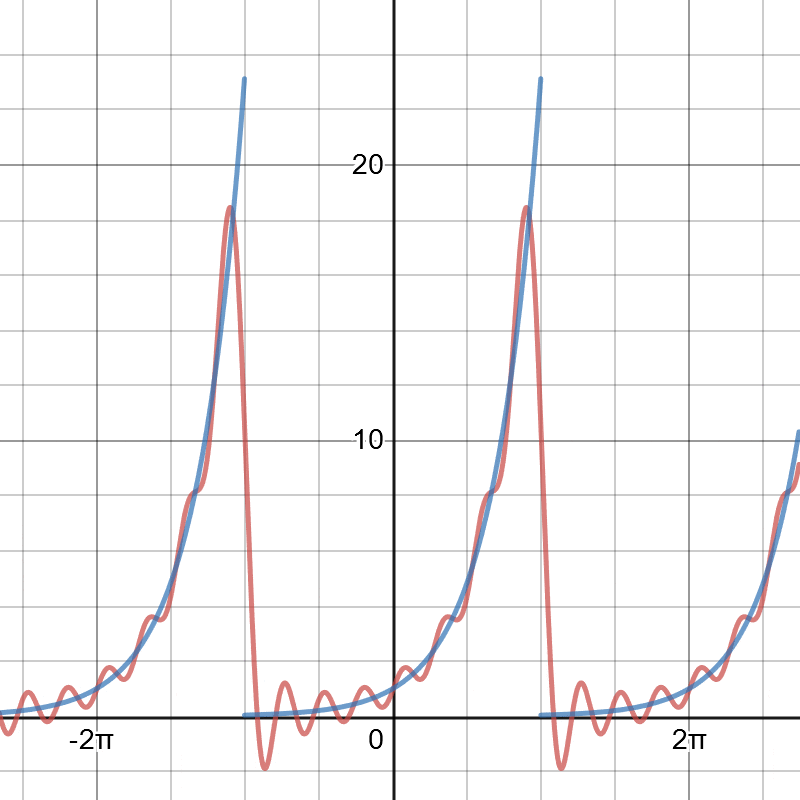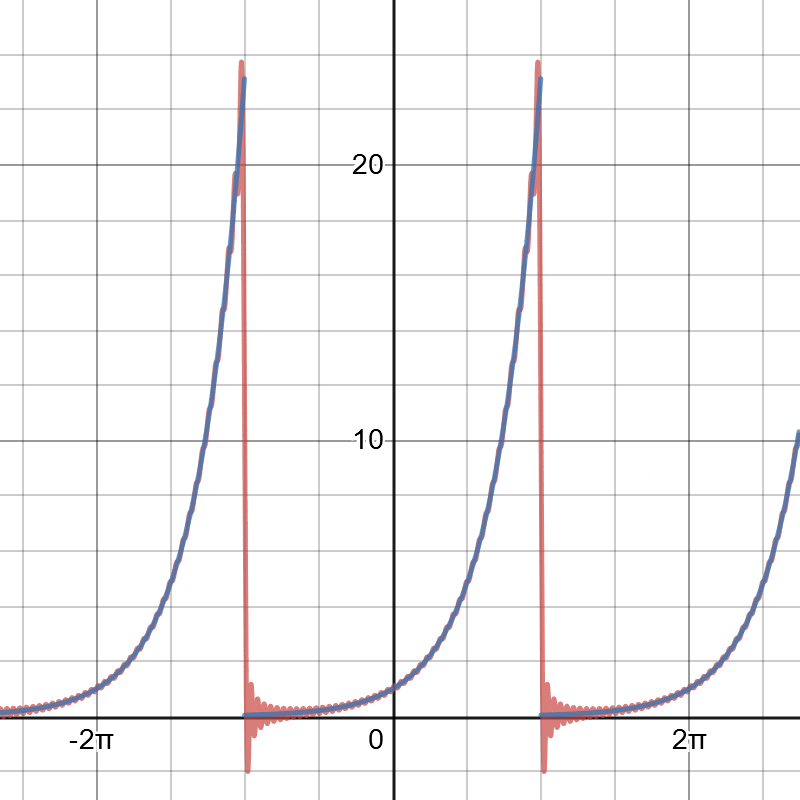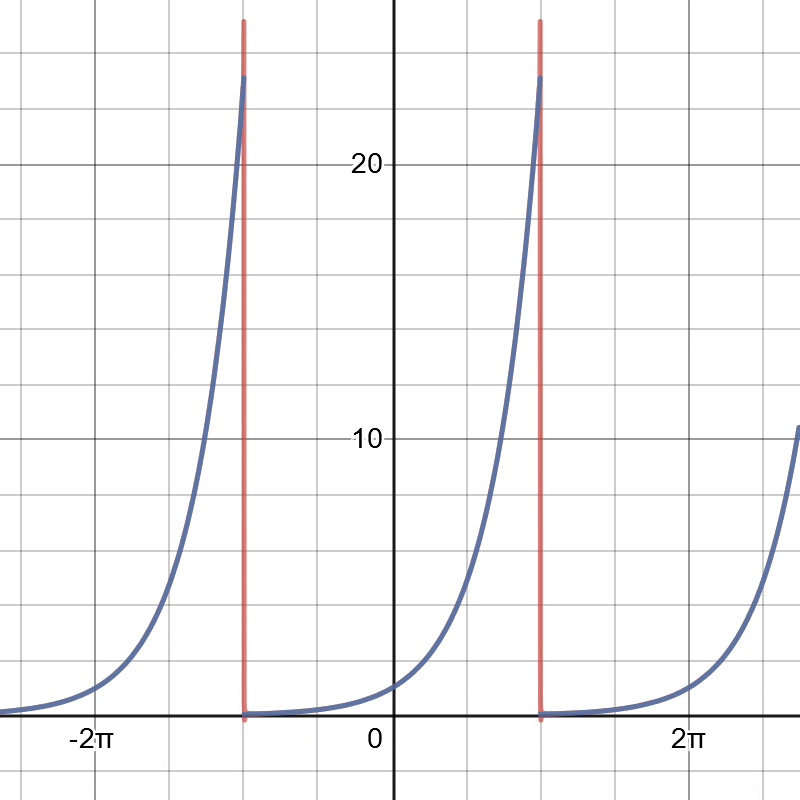
푸리에 급수를 사용하면 함수의 대칭성과 관계없이 "모든 주기함수"를 삼각함수의 합으로 나타낼 수 있다(물론 손으로 계산할 때는 적분이 용이한 형태의 함수가 선호됨....) 예제를 통해 푸리에 급수를 알아보는 건 여기까지 하고 다음 시간에는 푸리에 급수가 왜 저렇게 정의되는지(계수의 정의에 대한 증명)를 알아보자
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 4. 오일러 공식(Euler's Formula) (0) | 2020.12.05 |
|---|---|
| [공업수학] 3. 선적분(Line Integral) 예제 (0) | 2020.12.05 |
| [공업수학] 2. 라플라스 변환(Laplace Transform) 예제 (5) | 2020.12.05 |
| [공업수학] 0. 미분방정식의 소개 (0) | 2020.10.09 |
| ERWIN KREYSZIG의 공업수학 (0) | 2020.10.09 |