완전미분방정식이 무엇인지, 어떻게 판별하는지, 어떻게 푸는지에 대해서는 아래 링크를 참조바랍니다. 풀이과정이 다소 길고 복잡하기 때문에 예제 파트를 따로 나누었습니다. 이번 포스팅에서는 네 개의 미분방정식 예제를 소개하는데, 이를 통해 완전미분방정식에 대한 감이 잡히길 바랍니다..!
blog.naver.com/subprofessor/222094820066
(예제 1) 다음 미분방정식의 완전성을 검사하여라
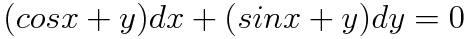
dx앞에 있는 놈들을 y에 대해 편미분해주고, dy앞에 있는 놈들을 x에 대해 편미분해줍니다.
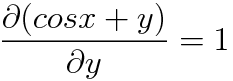
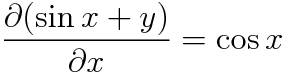
음! 뭔가 둘이 안맞네 하죠? 맞아요 완전미분방정식이 아닙니다. 이런 간단한 문제가 시험에 나올 일은 없지만 만약 나온다면 저는 이렇게 답안을 작성할 것 같네요
해당 미분방정식에 대해 완전성 검사를 시행한 결과
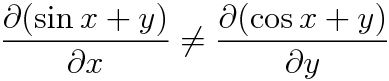
이므로 완전미분방정식이 아닙니다. 라고 말이죠
(예제 2) 다음 미분방정식의 완전성을 검사하여라
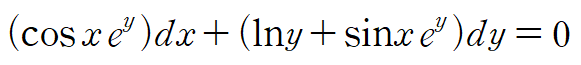
똑같이 dx 앞에 있는 애들을 y에 대해, dy 앞은 x에 대해 각각 편미분해서 비교합니다.
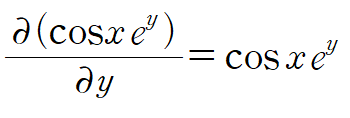
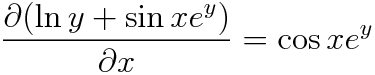
즉 두 편미분값이 같으므로 완전미분방정식입니다.
(예제 3) 다음 미분방정식의 해를 구하여라
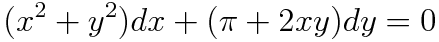
(a) 완전성 검사
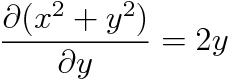
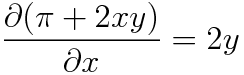
깔끔합니다. 넘어갑시다
(b) u 세우기
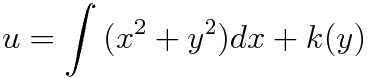
완전미분방정식의 해법 파트에서 배운대로 적용하면 위와 같이 u를 설정할 수 있구요 부정적분을 해주면 다음과 같은 식을 얻습니다.
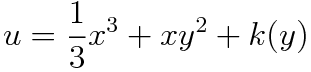
(c) y에 대해 편미분해서 k(y) 구하기
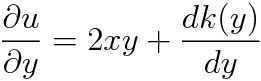
위에서 세운 u를 y에 대해 편미분한 것입니다.
이제 이것을 N(x,y)즉 처음에 주어진 미분방정식에서 dy앞과 비교해주면 됩니다.
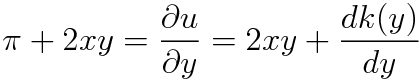
2xy가 깔끔하게 소거되므로 다음과 같은 과정을 통해 u를 구할 수 있습니다.
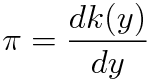
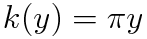
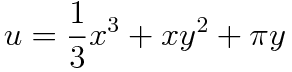
여기서 끝? u=C라는 관계식을 사용해 적분상수로 정리해주어야 합니다. 따라서 주어진 미분방정식의 해는 다음과 같습니다.
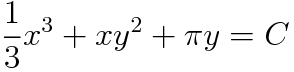
깔끔합니다.
(예제 4) 다음 초깃값 문제를 푸시오
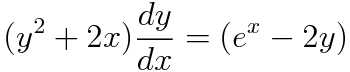
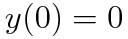
음.. 뭔가 우리가 그동안 보던 형태랑 차이가 있어보이죠? 겁먹을 필요 없이 dy와 dx를 분리해서 생각합시다.
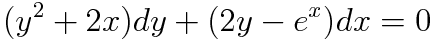
이제 완전성 검사를 시작합시다.
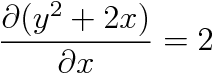
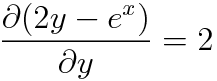
깔끔하네요. 이제 u를 세워봅시다.(이번에는 N을 가지고 풀어볼게요)
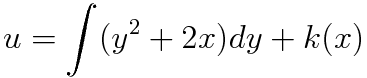
이렇게 세울 수 있겠죠? 부정적분을 계산해주면 다음 식을 얻습니다.
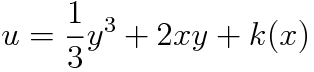
다음은 M(x,y)와 비교합시다.
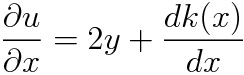
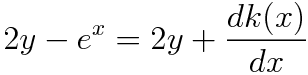
2y가 소거되므로 k(x)는 -e^x가 됩니다. u는 다음과 같이 정리할 수 있구요
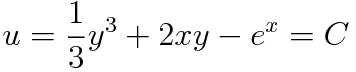
초깃값 y(0)=0을 대입하면 주어진 미분방정식의 특수해는 아래와 같습니다
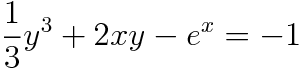
이제 좀 감이 오시나요? 완전성 검사부터 완전미분방정식의 해를 구하는 과정까지 네 개의 예시를 통해 알아봤습니다. 혹시 오타를 발견하셨거나 질문거리가 있으시면 편하게 댓글 달아주세요 :)
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 7. 디랙 델타, Short Impulse (0) | 2021.02.18 |
|---|---|
| [공업수학] 6. 편미분 방정식 : 라플라스 변환 해법 (1) | 2021.02.06 |
| [공업수학] 4. 오일러 공식(Euler's Formula) (0) | 2020.12.05 |
| [공업수학] 3. 선적분(Line Integral) 예제 (0) | 2020.12.05 |
| [공업수학] 2. 라플라스 변환(Laplace Transform) 예제 (5) | 2020.12.05 |