이전에 포스팅한 라플라스 변환은 f(t)에 관한, 즉 일변수 t에 대한 상미분방정식을 풀기 위한 해법으로써 소개되었다. 대수방정식을 거쳐 해를 구한다는 다소 편리한 이 라플라스 변환은 상미분방정식을 넘어 편미분방정식에도 적용될 수 있다(!).
편미분방정식을 라플라스 변환으로 풀기 위해서는 몇가지 기본전제(지식)가 필요하다.
1. 본 포스팅에서 다뤄지는 함수 w는 모두 이변수 함수 w(x,t)이다.
2. 라플라스 변환 시 적분은 한 문자에 대해서만 수행된다.
3. 역변환 또한 한 문자에 대해서만 수행된다.
4. W(x,s)는 함수 w(x,t)에 라플라스 변환을 수행한 함수이다.
편미분방정식에서 주의해야 할 것은 변수의 혼동이다. 라플라스 변환을 수행할 때 x와 t가 아무 관계 없는 독립변수이기 때문에 다른 한 문자를 상수취급하고 적분하면 된다. 도함수에 라플라스 변환을 취할 때도 동일하다.
이 해법은 기본적으로 상미분방정식에서 했던 것처럼 t에 대해 라플라스 변환을 취해 풀이해나가는 방식이다. x에 대한 변환은 소개하지 않는다.
과정을 정리하면 아래와 같다.
1. 주어진 편미분 방정식에 라플라스 변환을 취한다.
2. 초기조건을 사용해 식을 정리한다.
3. 정리된 식을 x에 대한 상미분방정식처럼 취급하여 해를 구한다. 여기서 해는 W(x,s)를 의미한다.
4. W(x,s)에 역변환을 취해 w(x,t)를 구한다.
(예제)
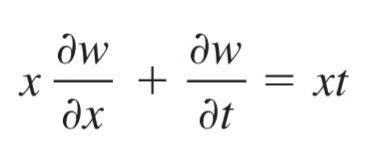
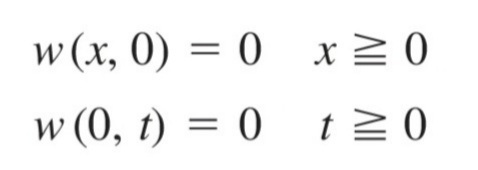
초기조건 (Initial Condition)과 경계조건 (Boundary Condition)이 주어졌다. 초기조건은 t=0일 때의 조건을, 경계조건은 x의 정의역 끝(위 문제의 경우 x=0)에서의 조건을 의미한다.
간단한 1계 편미분방정식이다.
<1> 먼저 양변에 라플라스 변환을 취하자
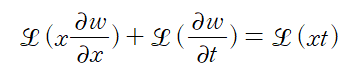
각 항별로 라플라스 변환을 수행하면 다음과 같다.
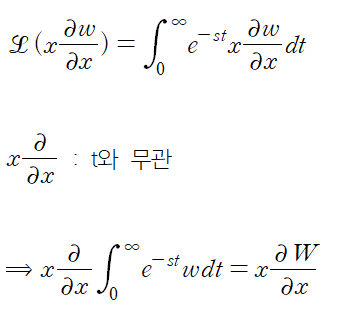
편미분 기호 x도 적분기호 앞으로 꺼내놓는다.
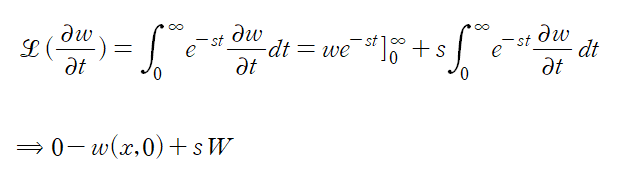
도함수의 라플라스 변환공식을 사용해도 좋다. 까먹었을 때는 직접 부분적분으로 유도하자
마지막으로 xt항이다. x를 상수취급하면 x/s^2 항을 얻는다.
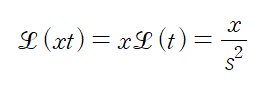
<2> 이상을 정리하면 아래와 같이 s와 x로 이루어진 방정식을 얻는다. 초기조건 w(x,0)=0 에 의해 항이 정리된다.

<3> x에 대한 1계 선형 상미분방정식을 풀듯 W(x,s)를 구한다.
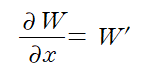
해를 구하는많은 방법들이 있지만 적분인자를 곱해서 푸는 방식을 채택.
먼저 W'의 계수를 1로 만들어주기 위해 양변을 x로 나눠주자
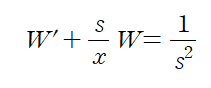
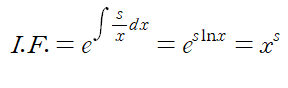
양변에 적분인자를 곱해주고 양변을 x에 대해 적분
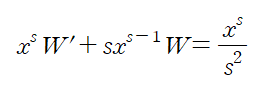
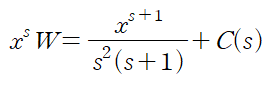
이때 적분상수는 s에 대한 C(s)로 설정해야 한다. x에 대한 편미분을 수행할 경우 s로만 이루어진 항은 모두 사라지기 때문에 C(s)의 형태로 설정하는 것인데, 이 C(s)는 초기조건 w(0,t)=f(t)로부터 W(0,s)=F(s)를 얻고, 대입하는 과정에서 결정된다.
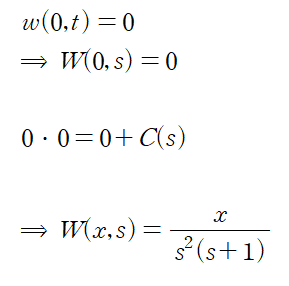
초기조건 w(0,t)=0의 양변에 라플라스 변환을 취하면 W(0,s)=0이 된다. 상미분방정식에서의 초깃값은 말 그대로 "값"이기 때문에 다른 액션을 취할 수 없지만 편미분방정식에서의 초기조건은 그 자체로 함수이기 때문에 갖가지 액션을 취할 수 있다.
<4> 역변환을 양변에 취하기 전에 역변환이 용이한 형태(부분분수)로 정리하자
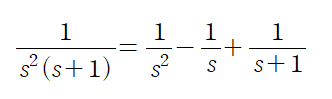
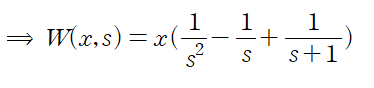
이제 마지막으로 양변에 역변환을 취해주자
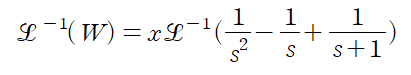
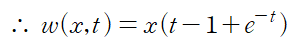
이렇게 라플라스 변환을 편미분에도 적용할 수 있다.
변수분리를 통해 풀 수도 있지만 라플라스 변환은 제차, 비제차 구분할 것 없이 적용할 수 있는 방법인 데다 풀이 중간중간에 적절한 경계조건을 사용하는 것이 제법 재밌는 편이다. RPG 퀘스트 하나씩 풀어가는 느낌이랄까
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 8. 합성곱(convolution) (2) | 2021.03.01 |
|---|---|
| [공업수학] 7. 디랙 델타, Short Impulse (0) | 2021.02.18 |
| [공업수학] 5. 완전미분방정식 예제 (2) | 2021.01.17 |
| [공업수학] 4. 오일러 공식(Euler's Formula) (0) | 2020.12.05 |
| [공업수학] 3. 선적분(Line Integral) 예제 (0) | 2020.12.05 |