사실 공업수학에서 미분방정식의 해를 구하기 위해 사용하는 방법이지만 별도로 미분적분학에 먼저 포스팅한다.
라플라스 변환은 미분방정식을 대수방정식 꼴로 변환시켜 보다 쉬운 방정식을 풀 수 있다는 이점을 가지고 있는 변환법이다.
대수방정식은
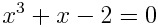
이런 애들을 칭하는 말이다. 대수적인 특성을 가지고 있는 방정식을 의미하며(당연히..) 사칙연산을 통해 해를 구할 수 있는 방정식을 의미한다. 미분방정식은 미분개념과 적분개념이 모두 포함되어 있는 방정식인데, 이 방정식은 애초에 사람이 인지하기가 어렵다. 변화율을 인지하는 것 자체가 어렵기도 하고 지수함수나 삼각함수와 같은 초월함수들이 포함될 경우 더더욱 이해하기가 어렵다. 반면 대수방정식은 인수분해 또는 근의 공식을 통해 쉽게 해를 구할 수 있다는 장점이 있다. 또한 대수방정식의 해를 구하는 과정에서 자연스럽게 초깃값이 사용되므로 해의 형태가 일반해가 아닌 특수해 형태로 나온다는 장점이 있다.(미지상수가 없다는 뜻!)
라플라스 변환을 통해 미분방정식을 대수방정식으로 바꾸고, 대수방정식의 해를 구한 다음 다시 라플라스 역변환을 통해 원래 미분방정식의 해를 얻을 수 있다. 라플라스 역변환은 간단히 대수방정식을 다시 미분방정식으로 바꾸는 것을 말한다

미분방정식의 해를 구하기 위해서는 두 가지 공식을 사용한다. ①기본 변환표, ②미분공식. 추가적으로 적분공식도 올려놓는다
s-shifting 이나 t-shifting 에 대해서는 따로 언급하지 않겠다. 보다 자세히 다루는 것은 추후 공업수학에서 포스팅할 때이지 않을까 싶다
(0) 라플라스 변환의 정의
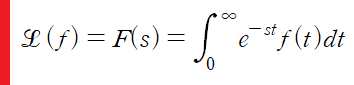
라플라스 변환의 정의
이 정의를 이용해 시간에 대한 함수 f를 s라는 새로운 변수에 대한 함수 F로 변환시킬 수 있다. 물론 F(s)=f(t)를 의미하지는 않는다. s와 t 사이에는 어떠한 관계도 성립하지 않기 때문에.
예시를 통해 라플라스 변환을 더 알아보자


이에 더해 라플라스 변환이 가지고 있는 매우 중요한 성질, 선형성 또한 유도해보자
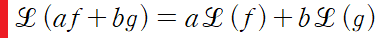
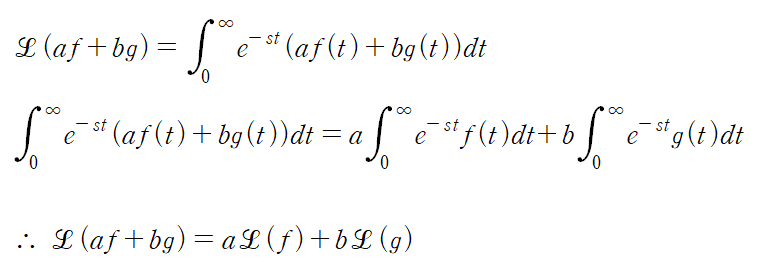
미분방정식은 대개 여러 개의 항으로 구성되어있기 때문에 선형성을 가진다는 사실을 알고 있어야 정상적으로(정석적으로) 해를 구할 수 있다
(1)
라플라스 변환표erwin kreyszig 의 advanced engineering mathematics 10th edition


공식이 더 있긴 한데 이정도면 충분하다. 나머지는 미분공식, 적분공식으로 직접 구할 수 있는 것들이다. 왼쪽에 F(s)가 위치한 이유는 위 테이블을 가지고 역변환 하라고.
(2) 미분공식, 적분공식
미분방정식은 함수f의 도함수가 포함되어있는 방정식이다. 따라서 미분방정식을 라플라스 변환을 통해 풀 때 도함수에 대한 라플라스 변환을 수행하는 것은 필수적이다. 추가적으로 적분에 대한 공식 또한 미분공식의 유도과정과 같은 방식으로 유도할 수 있다
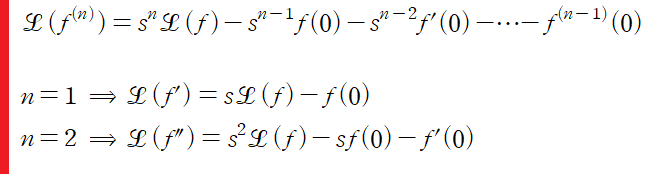
유도 과정은 다음과 같다
먼저, 1계 도함수에 대한 유도 과정이다
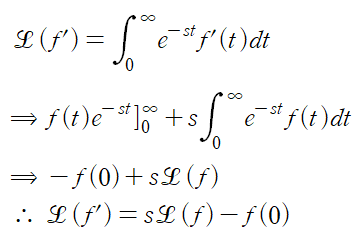
다음으로 n계 도함수에 대한 유도과정이다


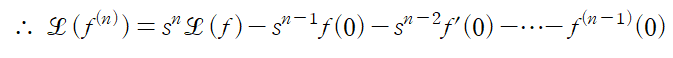
+) 적분공식

(3) 라플라스 변환을 이용해 미분방정식 풀기
(예제 1)
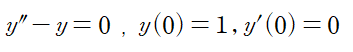



(예제 2)
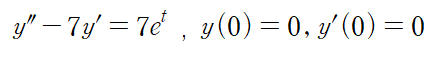

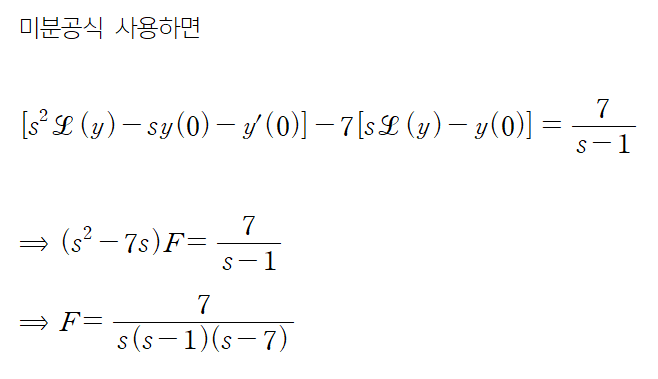
기본적으로 변환표를 이용하기 위해서는 부분분수 합 꼴로 변환해주어야 한다


Any Qustions, Any Comments WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 4. 오일러 공식(Euler's Formula) (0) | 2020.12.05 |
|---|---|
| [공업수학] 3. 선적분(Line Integral) 예제 (0) | 2020.12.05 |
| [공업수학] 1. 푸리에 급수 (Fourier Series) (1) | 2020.11.25 |
| [공업수학] 0. 미분방정식의 소개 (0) | 2020.10.09 |
| ERWIN KREYSZIG의 공업수학 (0) | 2020.10.09 |