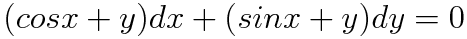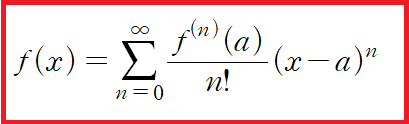매년 10월 말 그리고 12월 중순 즈음 되면 많이들 물어보는 게 이 합성저항이다. 정말 말도 안되게 간단하지는 않지만.. 이걸 돈주고 물어보는 분들이 매년. 매우. 많다는 사실에 조금은 울적하다(a little salty ☆) 컴팩트하게 가보자. 직렬은 도선을 따라 연결한 것, 병렬은 새로운 도선을 깐 것(이 경우 교차점이라 번역되는 node가 생성)이라 이해하자 간단하다. 회로분석은 저항에 흐르는 전류의 양을 계산하고 소비되는 전력을 분석하는 것을 기초로 이뤄진다. 근데 가끔 혹은 때때로 하나하나 계산하기가 어려울 때가 있다 이런 놈들을 상대할 때 일일이 각개전투를 하고 앉아있을 시간이 없다!(실무에선 띡띡 하나씩 교환한다..) 적어도 책상에 앉아 펜을 놀리는 우린 그렇다. ..