오늘은 무한급수의 합이 수렴하는지, 발산하는지 알 수 있는 판정법(Test) 중 교대급수 판정법(alternating series test)에 대해 알아봅시다.
(i)교대급수의 정의

교대급수는 양항 급수 즉 모든 향이 양수인 수열 an을 통해 정의됩니다. alternating 이라는 말에서도 알 수 있듯이 양수항과 음수항이 교대로 번갈아 나온다고 해서 교대급수라 합니다. 교대급수 판정법은 그러한 교대급수에 대해서 수렴과 발산을 조사할 수 있는 판정법입니다. 일단 조건 자체가 굉장히 간단하기 때문에 예제를 풀어보는 데에 문제는 없으나.. 대학교 시험문제의 경우 삼각함수 꼴로 교대급수가 주어질 수 있어 "어?? 이건 뭐지??"하고 어리버리 타지 않도록 합시다.
(ii) 교대급수 판정법

교대급수 판정법의 정의
그러니까 한마디로, 양항수열 an이 0으로 수렴하는 감소수열일때 해당 an으로 만든 교대급수가 수렴한다는 겁니다. 정의 자체가 그렇게 어렵지도 않고 예시에 적용하기도 그렇게 어렵지 않습니다. 그런데 한 가지 특수한 경우가 있습니다. 첫번째 조건에서 "모든 자연수 n"대신에 "어떤 자연수 k가 있을때,

"인 경우도 가능합니다. 이 경우는 곧 나오는 예제에서 알아봅시다. 교대급수 판정법은 적용이 그렇게 어렵지 않기 때문에 그냥 정의대로 정직하게 사용해주시면 됩니다.
(iii)예제
(예제 1) 다음 급수의 수렴/발산을 조사하여라

네 딱봐도 교대급수의 형태를 띄고 있는 급수가 주어졌습니다. 교대급수 판정법의 정의에 따라서 차근차근 풀어봅시다.
모든 자연수 n에 대하여 다음이 성립합니다.
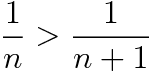
따라서 모든 자연수 n에 대하여
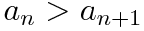
이 성립합니다. 또한

이므로 교대급수 판정법에 의해 주어진 급수는 수렴합니다.
(예제 2) 다음 급수의 수렴/발산을 조사하여라

교대급수 판정법의 첫번째 조건에서 무조건 모든 n에 대해 성립할 필요는 없다고 했지요? 이를테면 3보다 큰 모든 자연수에 대해서

가 성립해도 괜찮다는 겁니다. 주어진 수열이 감소하는지 알아보기 위해서 an을 가지고 함수f(x)를 만들어볼게요
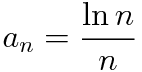
an을 위와 같이 정의합시다.

이렇게 f(x)를 설정해주고 f(x)의 도함수를 통해 f(x)의 증감을 알아봅시다. f(x)를 미분해 주면 아래와 같습니다.
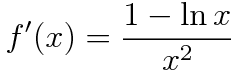
즉 f'(x)는
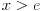
에서 0보다 작고, 따라서 f(x)는
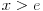
에서 감소합니다
따라서 f(x)의 모티브가 되는 an 또한
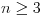
에서 감소함을 알 수 있는데요
따라서 3보다 크거나 같은 모든 자연수 n에 대하여 다음이 성립합니다

다음으로 lim an을 조사해봐야 합니다. 아래와 같이 0임을 알 수 있는데요,
저는 간편하게 로피탈의 정리를 이용해서 극한값을 구해주었습니다
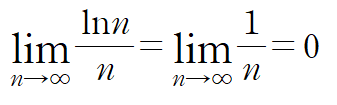
따라서 교대급수 판정법에 의해, 주어진 급수가 수렴함을 알 수 있습니다.
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 야코비안(Jacobian) 예제 (0) | 2021.02.06 |
|---|---|
| [미분적분학] 이상적분 (Improper Integral) (1) | 2021.01.17 |
| [미분적분학] 삼각치환법 (Trigonometric Subtitution) (0) | 2021.01.17 |
| [미분적분학] 테일러 급수전개 (0) | 2020.12.06 |
| [미분적분학] 벡터함수의 미분 (0) | 2020.10.09 |