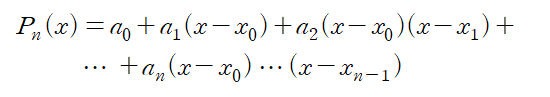그린정리는 폐곡선 C를 경로로 취하는 선적분(Line Integral)과 C로 둘러싸인 영역 D의 중적분(Double Integral) 간의 관계를 부여하는 정리라고 할 수 있습니다. 정리를 소개하기 이전에 곡선 C의 양의 방향(positive orientation)을 시계반대방향(counterclockwise, CCW)으로 정의하겠습니다. 1. 그린정리 (Green'sTheorem) 보통은 C가 폐곡선이기 때문에 아래와 같은 식으로 그린정리를 소개합니다. D는 앞서 소개했듯이 C로 둘러싸인 영역입니다. 그린정리를 간단히 설명하자면 다음과 같습니다. 곡선 C가 매끄럽고 양의 방향을 가지며 평면 상의 폐곡선일 때 C로 둘러싸인 영역을 D라고 하자. 이때 F = 로 표현되는 벡터함수다. ..