SUBORATORY

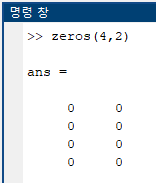
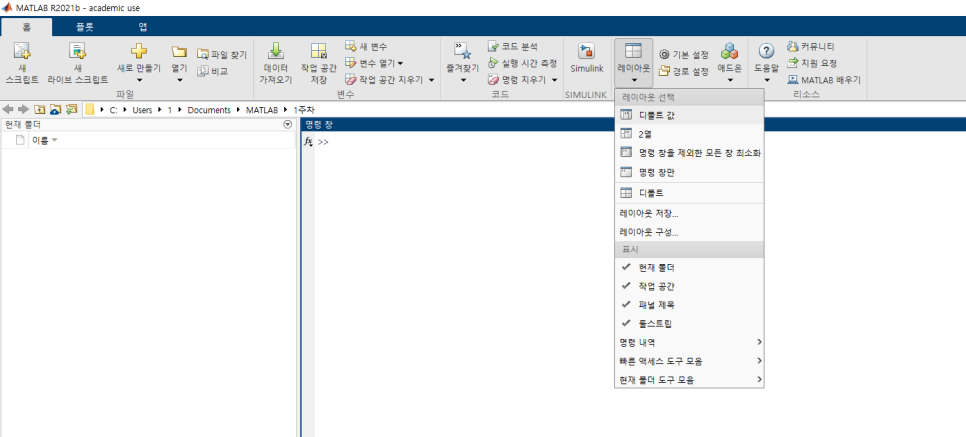
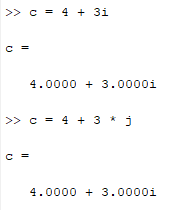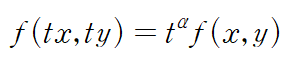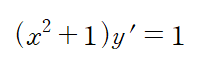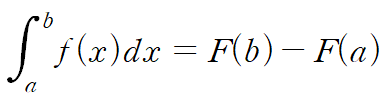#매트랩 ​ ​ 1. zeros ​ zeros(r, c)를 입력하면 모든 entry가 zero이고 크기가 r x c 인 배열(행렬)이 생성된다. ​ ​ zeros(n, n)를 입력하면 모든 entry가 zero이고 크기가 n x n 인 배열이 생성된다. ​ ​ ​ ​ 2. ones ​ ones(r, c) 를 입력하면 모든 entry가 1이고 크기가 r x c 인 배열이 생성된다. ​ ones(n) 를 입력하면 모든 entry가 1이고 크기가 n x n 인 배열이 생성된다. ​ ​ 3. Colon Operator (:) ​ Colon operator는 파이썬의 슬라이싱과 유사한 기능이다. ​ 아래 그림은 새로운 배열을 생성하고 colon operator를 사용한 예시이다. ​ :가 범위에 해당하는 건데 :..

#매트랩 ​ ​ 1. 사칙연산 (Mathematical Operation) ​ 연산자 설명 예시구문 ^ 거듭제곱 4^2 = 8 * 곱셈 3*pi = 6.2832 / 나눗셈 4/2 = 2 + 덧셈 3 + 5 = 8 - 뺄셈 3 - 5 = -2 파이썬에서 거듭제곱이 **로 표현되는 것과 다르게 매트랩에서는 ^​을 사용한다. ​ ​ ​ ​ 2. Array entries ​ 생성한 배열의 엔트리는 A(2,3)과 같이 출력할 수 있다. ​ 다음과 같이 3 x 4 array(matrix) 를 생성한 후 ​ A(2,3)을 명령 창에 입력하면 2행 3열에 해당하는 entry가 출력된다. ​ ​ ​ 만약 행렬의 크기를 벗어난 행이나 열을 입력할 경우 Error가 출력된다. ​ ​ ​ A(3)처럼 행 개수 내의 범위에 해..

#매트랩 ​ ​ 1. 복소수 복소수는 i 또는 j를 이용해 별도의 기호없이 표현한다. i 대신 j를 사용하는 것은 전류 i 와 혼동되는 것을 피하기 위함이며 3i 라고 쓰는 것과 3*i 라 쓰는 것은 같다. ​ ​ ​ 2. format 매트랩은 기본적으로 수를 소수점 아래 4자리까지 표현한다. 이러한 수의 표현 형식을 format이라 하며 기본형식은 short, 소수점 아래 14 에서 15자리까지 표현되는 것을 long, 공학적 표기방식은 short eng 이다. ​ format short ​ 같은 x에 대해 format long을 입력하고 난 뒤의 값은 조금 차이가 있다. format long ​ x*3을 수행했을 때 1이 반환되기 때문에 short냐 long에 따라 0.3333 이나 0.3333333..

#매트랩 ​ ​ 1. 변수 지정​ ​ 파이썬의 바인딩과 동일하게 등호(=)기호를 사용해 원하는 변수에 값을 지정할 수 있다. ​ 변수를 지정할 때는 몇 가지 룰이 있는데 잘못 지정한 경우 친절하게 알려주니까 외울 필요는 없다. (1) a123과 같이 문자와 숫자를 함께 변수의 이름으로 사용할 수 있지만 123a처럼 숫자가 맨 앞에 오는 것을 불가능하다. 맨 앞에 오는 것은 반드시 알파벳이어야만 한다. ​ ​ (2) 변수의 이름으로 사용할 수 있는 특수문자는 "_" , 통칭 언더바(underscore) 가 유일하다. 이때 언더바의 개수에는 딱히 제한이 없다. ​ ​ ​ 2. 배열(array) ​ 매트랩에서 파이썬의 리스트 자료형과 유사한 배열(array)을 생성할 수 있다. ​ ​ 배열을 생성하려면 대괄호..

#매트랩 ​ ​ 1. 레이아웃 ​ ​ 초기 실행화면에서 상단의 레이아웃 버튼을 선택하면 여러가지 원하는 레이아웃을 적용할 수 있다. ​ ​ ​ 또한 기호에 맞추어 설정한 레이아웃을 저장할 수도 있다. 나는 내가 원하는 기본 레이아웃을 "디폴트"라는 이름으로 저장했는데 저장한 레이아웃은 '레이아웃 저장' 버튼 위에 위치한다. 저장한 레이아웃을 '레이아웃 구성' 버튼을 눌러 이름을 바꾸거나 삭제할 수 있다. ​ ​ ​ 2. 명령 내역 명령 내역에서 도킹됨을 선택하면 화면 우측 하단에 지금까지의 명령이 기록되는 time line 같은 창이 생긴다. 명령 내역을 우클릭해서 복사, 삭제 등 원하는 작업을 수행할 수 있다. ​ 원하는 명령을 더블클릭해서 명령 창에서 다시 실행할 수도 있다. ​ ​ 3. 편집기 ​ ..

​ ​ 반복되는 일상 속에서 되풀이 하는 일들을 크게 두 가지로 구분합니다. 그 일이 나를 파괴한다면 우리는 그 일을 버릇이라 부르고, 나를 빛나게 한다면 우리는 그것을 습관이라 부릅니다. 인생을 살아가는 데 있어서 나쁜 버릇을 제하고 좋은 습관들을 정착시키는 것이 중요하다는 사실은 너나 할 것 없이 모두가 알고 있는 사실입니다. ​ 하지만 우리는 습관이니, 버릇이니 돌아볼 겨를도 없이 바쁜 시간 속에서 치여 살아갑니다. 그런 현대인에게(특히 성미 급한 한국인에게 참 좋은 방법이라고 생각합니다) 저자 제임스 클리어가 제안하는 방법은 너무나 획기적이어서 실천으로 옮기지 않을 수 없습니다. ​ 내용 요약 별 건 아니고 이라는 제목에 걸맞게 아주 작은 습관을 반복해나가는 것입니다. 'atom'은 눈에 보이지도..

#공업수학 ​ 이전 글에서 1계 미방은 네 가지만 알면 된다고 했는데 추가로 지금까지 블로그에서 다루지 않은 두 가지 형태를 더 소개합니다. ​ (1) Homogeneous Equation 실수 α 에 대해 위 꼴로 정리되는 함수 f(x,y)를 동차함수(homogeneous function)이라 합니다. ​ 아래와 같은 미분방정식에 대해 ​ M과 N이 모두 동차함수인 것을 동차미분방정식 이라 합니다. ​ ​ ​ dx 앞에 붙은 함수의 동차성 검증 ​ dy 앞에 붙은 함수의 동차성 검증 ​ 위 방정식의 경우 M(x,y)와 N(x,y) 가 모두 2차 동차함수(homogeneous function of degree 2) 라 부릅니다. ​ 만약 M과 N이 모두 동차함수이며 그 차수가 동일하다면 u = y/x 또..

ㄴ #공업수학 ​ 1계 상미분방정식은 네 가지 형태만 알면 됩니다. P(x)dx = Q(y)dy 꼴로 표현가능한 변수분리형과 M(x,y)dx + N(x,y)dy = 0 꼴의 완전미분방정식, y' + P(x)y = r(x) 꼴인 선형 상미분 방정식, y' + p(x)y = r(x)y^a 꼴의 베르누이 방정식. ​ ​ (1) 변수분리형 https://blog.naver.com/subprofessor/222094390913 [공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식) 드디어 시작이다. 간단한 변수분리형 1계 상미분 방정식을 풀어보자. 1.2는 방향장(direction field)에 관... blog.naver.com ​ ​ 위와 같이 각 변수로만 묶이도록 양변을 정리하여 적분할 ..

Cory Wong - Cosmic Sans (feat. Tom Misch) bass score / bass tab / pdf ↓ 악보 출처 ↓ https://www.youtube.com/watch?v=Mh89hr54B2Q ↓원곡 ↓ https://www.youtube.com/watch?v=GgvMSSiZMi8

정적분의 값을 구하는 방법은 피적분함수의 원시함수(역도함수, Antiderivative)를 구해 구간의 끝 값을 대입하는 것입니다. ​ 이를테면 처럼 ​ 그런데 일반적인 방법으로 Antiderivative를 구할 수 없는 함수에 대해서는 정적분을 어떻게 구해야 하는가? 라는 물음이 생겨나는데 아래와 같은 경우를 살펴봅시다. ​ 마땅한 Antiderivative를 구하기가 어렵습니다. 해서 f(x)와 근접한 다항함수 P(x)를 찾아 그것의 정적분으로 f(x)의 정적분 값을 근사하는 것이 뉴턴-코츠 공식입니다. ​ ​ ​ 1. 사다리꼴 (Trapezoidal Rule) 작은 도형으로 쪼개서 그 넓이를 구한다. 라는 개념은 고등학교 과정에서도 배우는 구분구적법 내용입니다. ​ 사다리꼴 공식은 각 점을 잇는 선..