1. 일변수함수의 극대, 극소
다변수함수를 살펴보기 전에 일변수함수에서의 극대, 극소를 살펴봅시다

미분가능한 함수에 대해서 극값이 존재하는 조건은 f'(x)=0 이고 f''(x)>0 또는 f''(x)<0 입니다. 고등학교에서도 배운 내용이지만 "f'(x) 좌우에서 부호변화가 있어야 한다"라는 익숙한 말을 이계도함수로 표현하면 위와 같습니다.
위 그래프 f(x)는 x=c에서 극대인데 이것은 x=c에서 f'(c)=0 이고 f''(c)<0 이기 때문입니다. 또한 x=d에서 f'(d)=0 이고 f''(d)>0 이기 때문에 극소입니다.

y=x3의 경우 x=0에서 f'(x)=0이지만 f''(x) 또한 0이기 때문에 극값을 갖지 않습니다. x=0은 변곡점(Inflection Point)이라고 부릅니다.
2. 다변수함수의 극대, 극소, 안장점

위 그림에서 z=f(x,y)라 하면 f(x,y)는 x=1, y=3 에서 극솟값 4를 가짐을 볼 수 있습니다. f(x,y)는 x=1, y=3 에서 x의 편도함수 fx와 y의 편도함수 fy가 모두 0임을 확인할 수 있습니다.

f(x,y)의 편도함수
그러나 다변수함수의 경우 편도함수의 값이 0이더라도 극값이 존재하지 않을 수 있습니다. 마치 y=x3 의 그래프처럼 말이죠. 다변수함수에서는 이러한 지점을 "안장점"(Saddle Point)이라고 합니다. 말 탈 때 쓰는 그 안장과 닮았다 해서 안장점이라는 이름이 붙여졌답니다.

위 그림에서 f(x,y)=y2-x2 는 x=0, y=0 에서 x, y에 대한 두 편도함수가 모두 0이지만 극값이 아닙니다.
다변수함수에서 극대, 극소의 정의는 다음과 같습니다

한국어로 풀이하면 (a,b)의 근방의 모든 (x,y)에 대해 f(x,y)≤f(a,b) 일 때 극대, f(x,y)≥f(a,b) 일 때 극소라 정의됩니다. 근방에 대한 정의는 생략하겠습니다. 단순히 (a,b) 주위의 모든 점이라고 생각하면 됩니다.
이제 fx=fy=0인 점에 대해서 극점인지, 안장점인지 판별하는 방법을 알아봅시다.

fx=fy=0인 점(a,b)를 임계점(Critical Point) 라고 하는데 이것이 극값, 안장점의 후보가 됩니다.
이 임계점들에 대해서 판별식을 통해 극값과 안장점을 결정합니다.
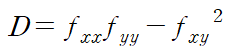
먼저 D>0인 경우 극값이 존재합니다. 이때 fxx가 0보다 크면 극소, 0보다 작으면 극대입니다.
다음으로 D<0인 경우 안장점입니다.
마지막 D=0인 경우는 극값과 안장점 여부를 판단할 수 없습니다.
(예제 1) f(x,y)의 극대, 극소, 안장점을 구하여라
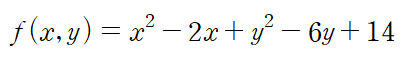
먼저 fx=fy=0 인 임계점을 찾아봅시다
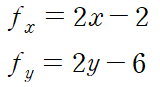
위 1계 편도함수로부터 임계점은 (1,3)이고 이것이 극소, 극대, 안장점의 후보가 됩니다
판별식 D를 사용하기 위해 2계 편도함수를 구합니다
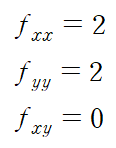
이때 모든점에서 D>0입니다
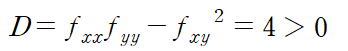
D>0이므로 극값이 존재하며
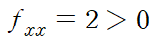
fxx가 0보다 크므로 f(x,y)는 (1,3)에서 극솟값 4를 가집니다
사실은 다변수함수의 극값, 안장점을 판별하는데 쓰이는 2계 편도함수식 D를 "헤시안 행렬식"이라고 부르는 게 맞습니다만 극값, 안장점을 "판별"하는 것이니 판별식이라고 부르겠습니다.
(예제 2) f(x,y)=x2-4xy+y3+4y 의 극대, 극소, 안장점을 구하여라
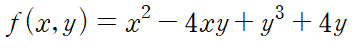
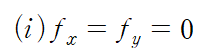
먼저 임계점을 구합니다.
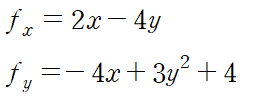
fx=0 으로부터
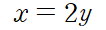
이것을 fy=0에 대입하면
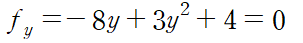
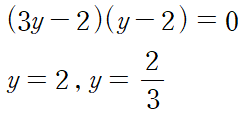
따라서 임계점은 다음 두 점입니다.
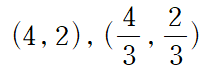
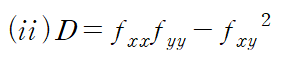
판별식에 임계점을 대입합니다.
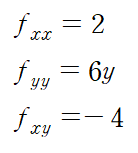
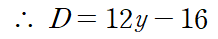
첫 번째 점을 대입하면
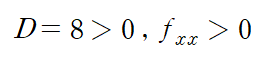
따라서 f(x,y)는 (4,2)에서 극솟값 -12 를 가집니다.
두 번째 점을 대입하면
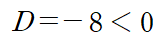
따라서 f(x,y)는 (4/3, 2/3)에서 안장점 32/27 를 가집니다.