그린정리는 폐곡선 C를 경로로 취하는 선적분(Line Integral)과 C로 둘러싸인 영역 D의 중적분(Double Integral) 간의 관계를 부여하는 정리라고 할 수 있습니다. 정리를 소개하기 이전에 곡선 C의 양의 방향(positive orientation)을 시계반대방향(counterclockwise, CCW)으로 정의하겠습니다.
1. 그린정리 (Green's Theorem)

그린정리는 폐곡선 C에 대한 정리이기 때문에 보통 아래와 같은 식으로 그린정리를 소개합니다. D는 앞서 소개했듯이 C로 둘러싸인 영역입니다.
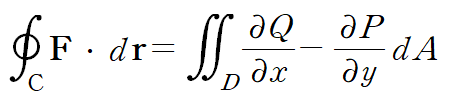
그린정리를 간단히 설명하자면 다음과 같습니다.
곡선 C가 매끄럽고 양의 방향을 가지며 평면 상의 폐곡선일 때 C로 둘러싸인 영역을 D라고 하자. 이때 F = <P, Q>로 표현되는 벡터함수다.

이때 P와 Q가 영역 D에서 편도함수를 가진다면 곡선 C에 대한 F의 선적분은 영역 D에서 Qx-Py 의 중적분과 같다.
2. 예제
(예제 1) 선적분을 계산하여라. C는 (0,0), (1,0), (0,1)을 잇는 삼각형이며, 양의 방향이다.
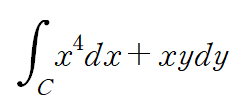

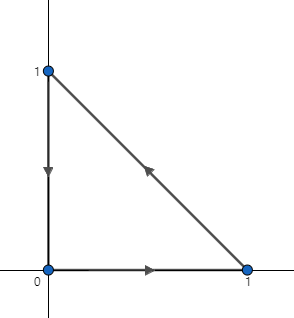
C를 xy 평면에 표시하면 다음과 같습니다. 선적분을 구하기 위해서는 세 개의 구간으로 방향벡터 r(t)를 쪼개어 계산해야 하는데 그린정리를 이용하면 한 번의 중적분으로 쉽게 계산할 수 있습니다.
그린정리를 사용하기 위해 P와 Q를 구하고 각각의 편도함수를 구합니다.
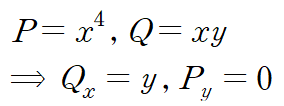

색칠한 영역 D는 아래와 같습니다.

그린정리를 이용해 선적분을 계산하는 대신 중적분을 계산합니다.
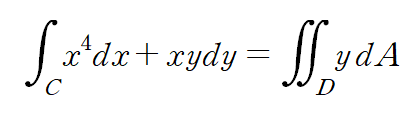
세 구간으로 C를 나누어 계산하는 것보다 훨씬 간편합니다.
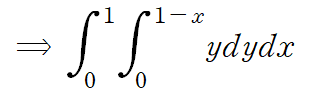
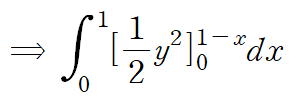
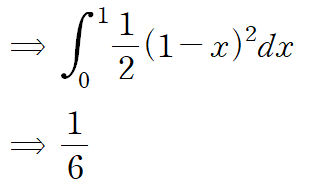
따라서 선적분의 값은 1/6 입니다.

(예제 2) xy 평면에 위치한 곡선 C가 중심이 원점이고 반지름이 3인 원일 때 선적분을 계산하여라

마찬가지로 그린정리를 이용해 중적분으로 바꾸어 계산해줍시다. 선적분으로 접근하기에는 함수가 너무 복잡한 형태입니다.
그린정리를 계산의 편이성이라는 측면에서 접근한다면 선적분에서 dx 앞에 오는 항을 y로 편미분한 것이 간단한 형태가 되는지 보면 됩니다. 마찬가지로 dy 앞에 오는 항을 x로 편미분한 것이 간단한 형태가 되는지 보면 됩니다.

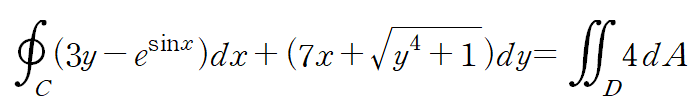
영역 D는 반지름이 3인 원이었으니 답은 36π 입니다.

(+) 중적분에서 피적분함수가 4인 경우 아래 식을 이용해 간단히 값을 구할 수 있습니다.
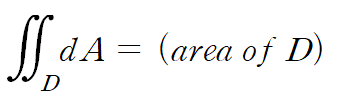
(예제 3) F(x,y)와 xy평면 상의 곡선 C가 다음과 같을 때
양의방향으로의 폐곡선 C에 대한 F의 선적분을 계산하여라


그린정리를 이용했을 때 간단한 형태의 중적분이 됩니다.
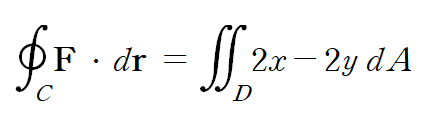
이를 계산하는 일련의 과정입니다.
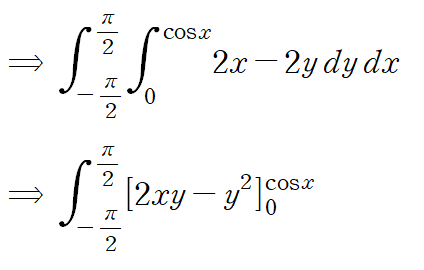
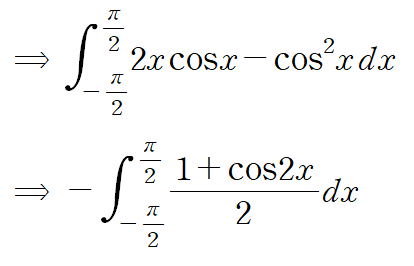
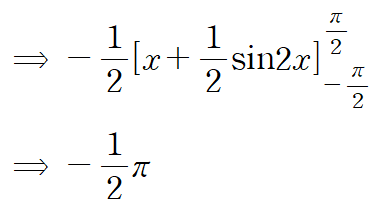
따라서 선적분의 값은 다음과 같습니다.
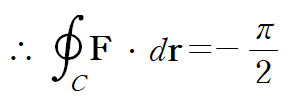
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.23 |
|---|---|
| [미분적분학] 라그랑주 승수법 예제 (0) | 2021.12.12 |
| [미분적분학] 다변수함수의 편미분, 연쇄법칙 (Chain Rule) (2) | 2021.11.08 |
| [미분적분학] Cylindrical Shell Method (4) | 2021.04.17 |
| [미분적분학] 이상적분 (Improper Integral) (0) | 2021.02.06 |