지난 시간 소개한 라그랑주 다항식에 이어 뉴턴 보간법과 분할차분(Divided Difference)에 대해서 알아봅시다.
https://subprofessor.tistory.com/63
[수치해석학] 라그랑주 다항식 (Lagrange Polynomial), 파이썬 코드
오늘 다룰 내용은 보간법의 일종인 라그랑주 다항식 입니다. 보간법(Interpolating)은 간단히 몇 개의 점이 주어졌을 때 그것을 관통하는 함수를 세워 discrete한 데이터들을 연속적인 데이터로 근사
subprofessor.tistory.com
보간법에 대한 설명은 위 링크로 대체하겠습니다.
1. Newton's Interpolating Polynomial
뉴턴 보간법은 다음과 같은 형태의 Polynomial 을 지칭합니다.
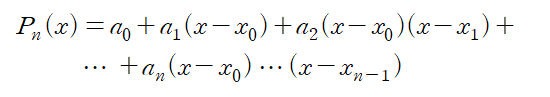
각 계수는 데이터로부터 얻어집니다.
Pn(x)를 (x0 · · · xn ) n+1 개의 데이터로 얻은 Interpolating Polynomial
f(x0) · · · f(xn)을 각 x에 대응하는 y 데이터라 합시다.
Pn(x)의 양변에 x0 을 대입하면 a0 를 얻습니다.
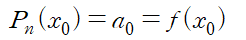
Pn(x)의 양변에 x1 을 대입하면
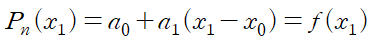
이때
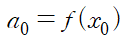
가 성립하므로
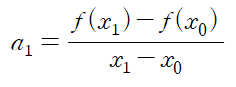
a1 은 위와 같습니다.
마찬가지로 모든 k ∈[0,n] 에 대해 양변에 xk 를 대입하는 것으로 ak 를 구할 수 있습니다.
2. Divided Difference
Divided Difference를 이용하면 다항식의 계수를 보다 간편하게 나타낼 수 있습니다.
Divided Difference(분할 차분)는 다음과 같이 정의됩니다.
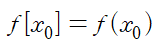
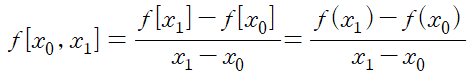
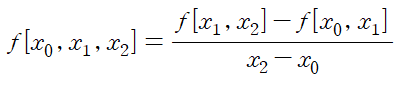
2nd divided difference
.
.
.
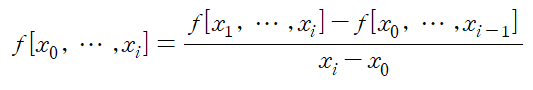
위에서 설정한 ak 가 곧 k th divided difference가 되어 뉴턴 보간법에서 다항식은 다음과 같이 정리됩니다.
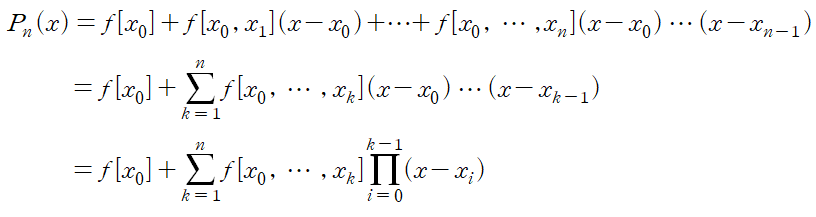
다음은 Divided difference가 정말로 계수가 되는지 확인해보기 위해서 a2 를 직접 구해보는 과정입니다.
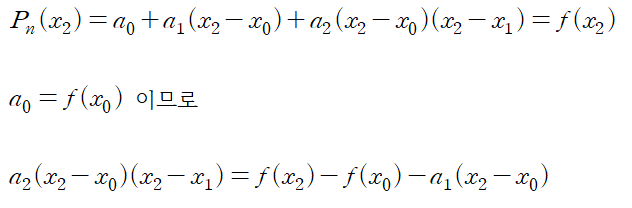
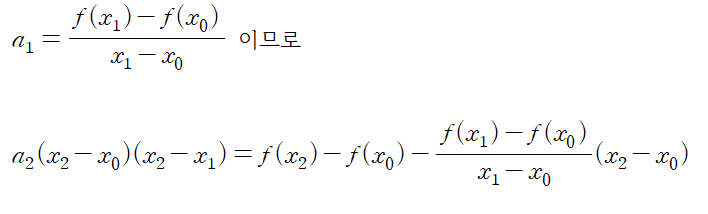
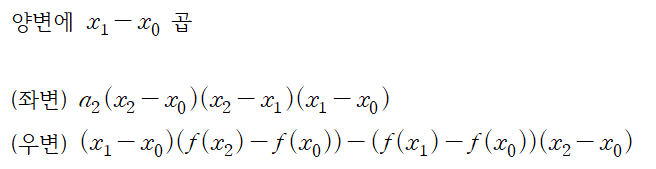
우변을 전개하면 f(x0)x0 항이 소거됩니다.
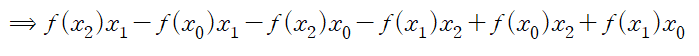
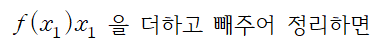
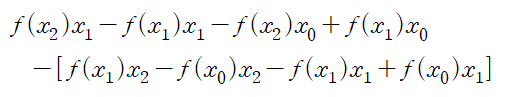
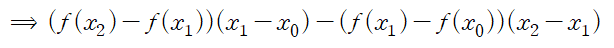
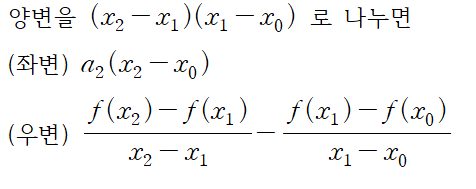
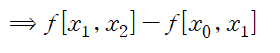
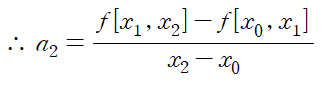
3. for same interval
x 데이터의 간격이 일정한 경우 보다 간단히 다항식을 얻을 수 있습니다. 실제 실험 시에는 시간 간격을 일정하게 두고 데이터를 얻는 경우가 많기 때문에 해당 방법을 알고 있다면 보다 쉽게 코드를 작성할 수 있습니다.
Interpolating Polynomial 은
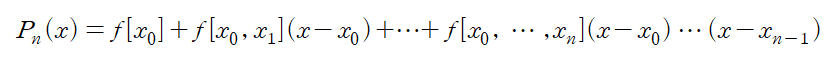
Divided Difference 는
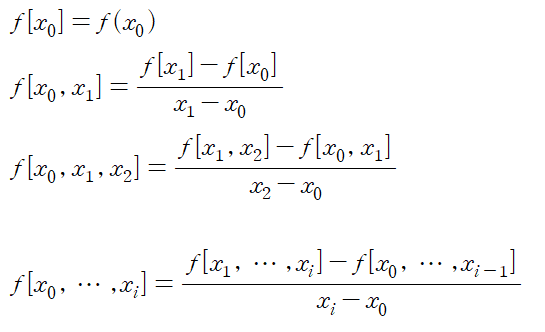
이때 인접한 두 데이터의 간격이 h라 하면 (xi - xi-1=0) 1st divided difference 는
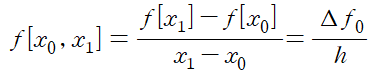
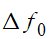
는
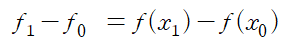
을 의미합니다.
마찬가지로 2nd divided difference 는
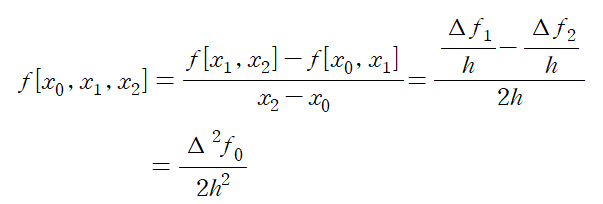
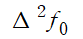
는
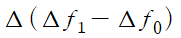
을 의미합니다.
같은 방법으로 k th divided difference 는 다음과 같습니다.
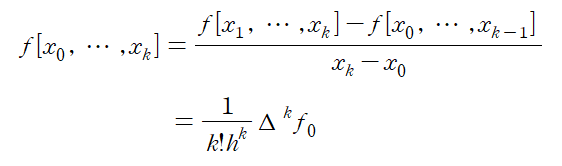
이때
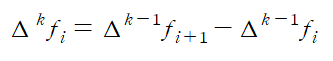
위와 같이 표현을 할 수도 있고, 이항정리와 유사한 형태로 표현을 할 수도 있습니다.
4. Binomial Theorem
마찬가지로 간격이 h로 일정한 경우를 다룹니다.
x를 x0 로 표현하면
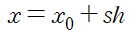
이것으로부터 아래 식이 성립합니다.
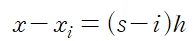
Interpoating Polynomial 은
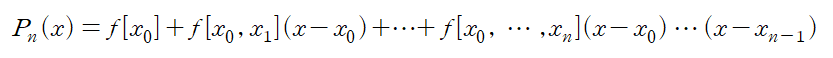
이때 x=x0+sh 가 성립하므로
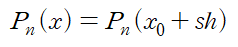
위 식의 우변은 Polynomial의 변수가 x에서 s로 바뀐다는 것을 내포합니다.
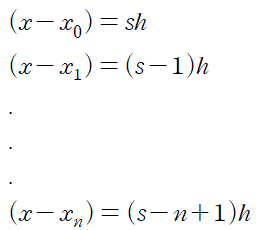
이므로
Interpolating Polynomial은 다음과 같습니다.
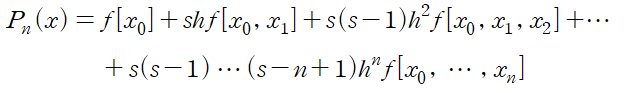
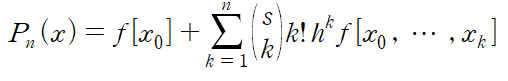
이때 k th divided difference가 아래와 같으므로

최종형태는 다음과 같습니다.
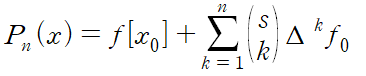
위 식을 (Newton's) Forward Diffence Formular 라고 합니다.
시그마 기호 바로 오른쪽에 있는 녀석은 Binomial coefficient(이항계수)라 하는데 고등학교 확률과 통계에서 나오는 조합 sCk 와 같습니다.
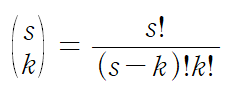
'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 비선형 회귀(Nonlinear Regression) 예제, 매트랩 코드 (0) | 2023.07.27 |
|---|---|
| [수치해석] 룽게-쿠타 방법(Runge-Kutta Method), 룽게 쿠타 4차 예제 (0) | 2023.06.08 |
| [수치해석학] LU분해(LU Factorization), 파이썬 코드 (1) | 2023.01.26 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |
| [수치해석학] 라그랑주 다항식 (Lagrange Polynomial), 파이썬 코드 (0) | 2021.12.08 |