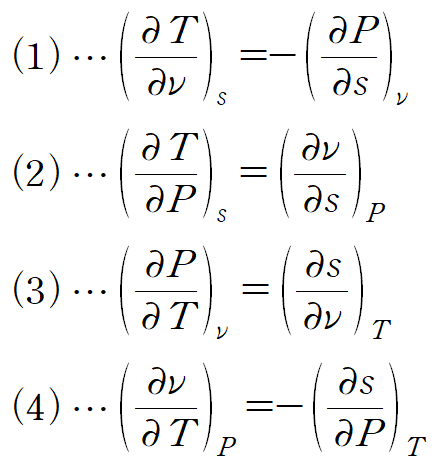SUBORATORY

#열역학 ​ Maxwell Relations 맥스웰 관계식은 네 가지 열역학 변수들에 대한 네 개의 관계식입니다. ​ ​ ​ ​ Example (예제 1) 다음 관계식을 이용하여 (∂T/∂v)s 를 유도하여라 ​ ​ ​ ​ 먼저, 유도해야 하는 식에서 s가 일정하다고 하니 ds = 0입니다. ​ ​ ​ 양변을 dv로 나누고 좌우변을 잘 정리하면 다음과 같이 원하는 관계식을 얻습니다. ​ ​ 문제의 요구사항과 어떤 변수가 상수인지를 먼저 확인하고 필요하다면 적절한 맥스웰 관계식을 사용해주어야 합니다. ​ ​ ​ ​ (예제 2) 깁스 관계식 du = Tds - Pdv 와 맥스웰 관계식을 이용해 P,v,T로만 표현된 (∂u/∂P)T 를 유도하여라. 또한 이상기체에서 이 편도함수가 어떤 거동을 보이는지 확인하여..

#유체역학 ​ ​ 유체가 파이프 내부를 지나갈 때 벽면과의 마찰 때문에, 또는 관이 꺾이거나 관의 형상이 바뀌는 지점(갑자기 좁아지는)에서 유체가 가진 에너지의 손실이 발생합니다. ​ 이때의 손실을 Major loss와 minor loss 로 구분하며 이번 게시글에서는 Major loss를 다룹니다. ​ ​ 1. Darcy Friction Factor Major loss는 유체와 파이프의 마찰 때문에 발생하는 손실이며 다음과 같이 수두(head)형태 즉 미터 단위(또는 ft, in) 로 표현됩니다. ​ 위 식을 "Darcy-Weisbach equation" 이라 합니다. ​ f는 darcy friction factor, l은 관의 길이, D는 관의 직경, V는 관을 지나는 유체의 속도(평균속도), g는 ..

#열역학 ​ Maxwell Relations 맥스웰 관계식은 압력(P), 비체적(v), 온도(T), 엔트로피(s) 사이의 관계를 나타내는 4가지 관계식이다. ​ 내부에너지(u)와 엔탈피(h)의 exact differential 에서 (1), (2) 식을 얻고 ​ Helmholtz function(A) 로부터 (3) 식을, ​ Gibbs function(G) 로부터 (4) 식을 얻는다. ​ ​ 이것이 모두 exact differential 이므로 우변에 존재하는 두 개의 미분소의 계수에 대해 다음이 성립한다. ​ ​ ​ 즉 (1),(2),(3),(4) 각각에 대해 이 성질을 적용할 수 있다. ​ ​ 위 네 가지 식이 바로 맥스웰 관계식이다. ​ ​ ​ Applications 맥스웰 관계식은 편미분방정식에서..

#유체역학 ​ Introduction 현실과 유사한 환경에서 실험을 수행하는 것은 시간과 물질적으로 어려움이 있고 무엇보다 비용적인 한계가 가장 크다. 공학은 "가장 경제적인 해결책"을 제시하는 학문이기 때문에 정확성을 최대한으로 유지하며 실험의 스케일을 축소하기 위해, 또한 구성요소들간의 상호작용 등을 최소화하는 간단한 모델이 등장했다. ​ ​ 공학에서 단위계는 힘-길이-시간 FLT system 과 질량-길이-시간 MLT system 두 가지가 있는데 이것은 모두 "차원"을 의미한다. ​ 예를 들어 밀도의 차원은 MLT system에서 다음과 같다. ​ ​ FLT system에서는 다음과 같다. ​ ​ 변수들은 각각의 고유한 차원을 가지고 있다. 각도(라디안), 레이놀즈 수 등 무차원 변수도 있다. ​..

#재료역학 ​ Introduction 부정정보(Statically Indeterminate Beams)는 정역학적으로 부정정(Indeterminate) 상태인 보를 의미합니다. ​ 부정정이란 평형방정식 ΣF = 0 만으로 반력을 확정할 수 없는 구조이며 부정정 문제를 풀기 위해서는 변위에 대한 관계식, 적합방정식 등 추가 관계식이 요구됩니다. 부정정보 문제의 예시는 다음과 같습니다. ​ 2차원 평형방정식에서 얻을 수 있는 식은 ΣFx = 0, ΣFy = 0, ΣM = 0 총 세 개인데 그림 (a)에 나타난 반력요소는 그보다 많은 4개이기 때문에 추가적인 관계식이 필요합니다. ​ ​ ​ 아래 그림의 경우 총 여섯 개의 반력이 발생합니다. ​ ​ ​ Analysis by Deflection Curve 이러한..

#재료역학 ​ ​ 가스가 든 탱크 등 용기 내의 압력이 외부보다 클 경우 용기에 발생하는 응력은 구형 용기와 원통형 용기로 케이스를 나누어 볼 수 있습니다. ​ ​ 1. Spherical Pressure Vessels 구형 압력용기를 아래 그림과 같이 반으로 잘라보면 중심을 포함하는 단면에서 압력에 의한 힘 P와 응력에 의한 힘 F가 작용합니다. ​ 압력에 의한 힘은 압력 X 단면적 이고 응력에 의한 힘은 두께t를 가지는 껍질의 중심까지의 반지름 rm을 사용해 산정하였습니다. ​ 이 두 힘이 평형을 이뤄야 한다는 것에서 용기에 작용하는 응력을 유도할 수 있습니다. ​ ​ ​ ​ ​ ​ ​ 2. Cylindrical Pressure Vessels 원통형 용기의 경우 원주방향(Circumference) 응력..

#재료과학 ​ ​ 목차 1. 처짐 미분방정식 2. 예제 풀이 ​ ​ ​ ​ ​ 보의 처짐 문제는 기본적으로 미분방정식으로부터 파생되는 적분상수들을 처리해줌으로 해결할 수 있습니다. 그 과정에서 제약조건들로부터 적분상수의 개수만큼 관계식을 이끌어 내는 것이 관건입니다. ​ ​ 1. 처짐 미분방정식 ​ ​ 최종적으로 얻고자 하는 건 처짐을 나타내는 처짐곡선 v입니다. 처짐 문제를 푸는 방법은 다음과 같습니다. ​ 1. SFD -> BMD 구하기(x에 대한 식으로 나타내기) 2. 적분해서 처짐곡선 구하기 3. 적절한 관계식 찾아서 적분상수 처리하기 ​ ​ ​ 하나의 문제에 대해 위 세 가지 미분방정식을 사용해 처짐곡선을 구해보고 그 다음 다양한 예제를 2계 미분방정식으로 해결해보겠습니다. ​ ​ 2. 예제 ​..

#재료역학 ​ ​ 1. Introduction 보의 처짐량은 v를 이용해 나타냅니다. v를 x의 함수라 할 때 미분방정식을 푸는 목적은 "처짐 곡선을 구하는 것"입니다. ​ ​ 처짐의 부호는 상향(U자형 커브)이 + 입니다. 즉 +y방향이 양입니다. ​ ​ ​ ​ 2. Derivation ​ mechanics of material, cengage 왼쪽 그림에서 미소 길이 ds 가 곡률반지름(radius of curvature) ρ 와 미소각변위 dθ 의 곱입니다. ​ ​ 곡률 k가 곡률반지름의 역수이므로 다음 식이 성립합니다. ​ 오른쪽 그림에서 처짐곡선의 기울이 dv/dx 는 tanθ 입니다. ​ ​ 이때 θ의 각이 매우 작다고 가정하면 두 가지 근사를 가정할 수 있습니다. ​ ​ (4) 식을 (3)에..

#재료역학 https://subprofessor.tistory.com/142 [재료역학] 보의 순수 굽힘 - 개념 편 #재료역학 순수 굽힘(Pure bending)이란 굽힘모멘트가 일정한, 즉 전단력이 작용하지 않는 굽힘을 뜻합니다. ​ 지난 글에서 SFD, BMD를 그릴 때도 설명했지만 전단력은 로 정의됩니다. ​ 굽힘모멘트 subprofessor.tistory.com ​ 지난 시간에 이어 보의 순수 굽힘을 알아보도록 합시다. 크게 다섯 가지 공식이 등장합니다. ​ ​ 이번 글에서는 간단하게 다섯 가지 공식의 의미와 각 공식들의 표현을 배워봅시다. ​ 공식 소개 (1) 변형률 ​ 중립면을 기준으로 높이 y에서의 보의 길이에 대한 축 방향(x축 방향) 변형률은 다음과 같습니다. ​ 마이너스 부호가 붙는 ..

#재료역학 순수 굽힘(Pure bending)이란 굽힘모멘트가 일정한, 즉 전단력이 작용하지 않는 굽힘을 뜻합니다. ​ 지난 글에서 SFD, BMD를 그릴 때도 설명했지만 전단력은 로 정의됩니다. ​ 굽힘모멘트가 일정하다면 dM/dx가 0이 되고, 따라서 전단력 V=0이 됩니다. ​ ​ ​ 이번 글에서는 중립면, 중립축, 보의 곡률과 같은 순수 굽힘 개념들에 대해 알아봅시다. 그 후에 추가적인 식 유도와 예제 풀이를 통해 익숙해지자구요 ​ ​ ​ ​ ​ 1. Definition (1) 직교 축 위 그림은 굽힘이 일어나는 보에 대해 x, y, z 축을 설정한 것입니다. 보의 축 방향이 x축이 되고, 옆에서 바라보았을 때 위로 올라가는 수직 방향(vertical)이 y축으로 설정됩니다. x, y 축이 설정되..