반응형
1. Introduction
보의 처짐량은 v를 이용해 나타냅니다. v를 x의 함수라 할 때 미분방정식을 푸는 목적은 "처짐 곡선을 구하는 것"입니다.
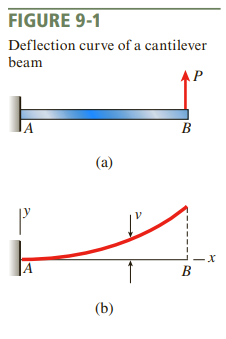
처짐의 부호는 상향(U자형 커브)이 + 입니다. 즉 +y방향이 양입니다.
2. Derivation
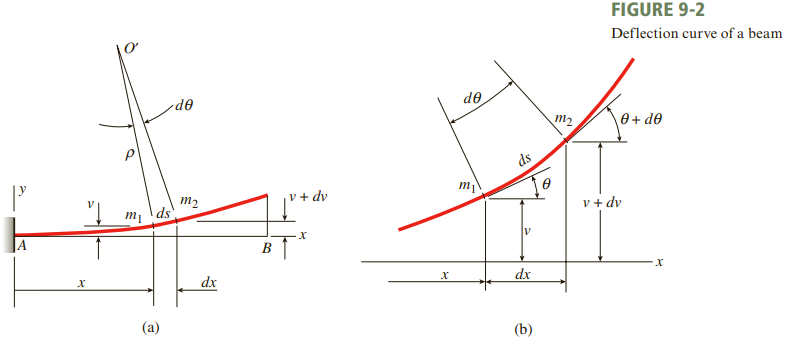
mechanics of material, cengage
왼쪽 그림에서 미소 길이 ds 가 곡률반지름(radius of curvature) ρ 와 미소각변위 dθ 의 곱입니다.

곡률 k가 곡률반지름의 역수이므로 다음 식이 성립합니다.
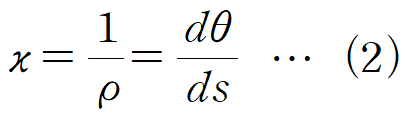
오른쪽 그림에서 처짐곡선의 기울이 dv/dx 는 tanθ 입니다.

이때 θ의 각이 매우 작다고 가정하면 두 가지 근사를 가정할 수 있습니다.
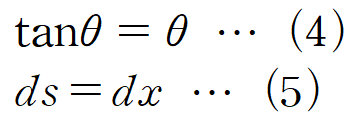
(4) 식을 (3)에 대입합니다.
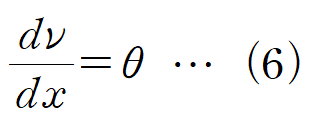
(5) 식을 (2)에 대입합니다.

이때 굽힘모멘트 M과 곡률 k의 관계는 아래와 같습니다.
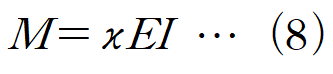
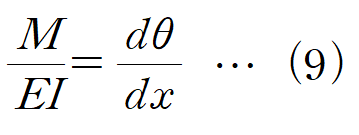
(6) 식의 양변을 x에 대해 미분합니다.

(9)와 (10)에서 dθ/dx 을 소거하면 처짐곡선의 미분방정식을 얻습니다.

(11)을 통상 아래와 같이 정리합니다.
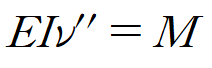
이 식에 굽힘모멘트, 전단력, 분포하중과의 관계식을 적용하여 3,4차 미분방정식도 유도할 수 있습니다.

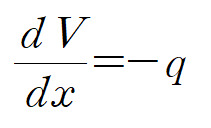
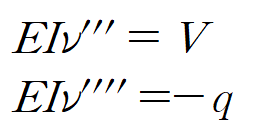
아래와 같이 세 종류의 처짐 곡선의 미분방정식을 유도하지만 통상 굽힘모멘트를 통한 2계 미분방정식을 사용합니다.

다음에는 처짐 예제와 모멘트 - 면적법에 대해 소개하는 시간을 갖겠습니다.
반응형
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 용기 내 압력에 의한 응력 (0) | 2023.02.24 |
|---|---|
| [재료과학] 보의 처짐 예제 (1) | 2023.02.24 |
| [재료역학] 보의 순수 굽힘 - 공식 편 (2) | 2022.12.31 |
| [재료역학] 보의 순수 굽힘 - 개념 편 (2) | 2022.12.26 |
| [재료역학] 전단력 선도, 굽힘모멘트 선도 예제 (SFD, BMD) (0) | 2022.12.26 |