#재료역학
Introduction
부정정보(Statically Indeterminate Beams)는 정역학적으로 부정정(Indeterminate) 상태인 보를 의미합니다.
부정정이란 평형방정식 ΣF = 0 만으로 반력을 확정할 수 없는 구조이며 부정정 문제를 풀기 위해서는 변위에 대한 관계식, 적합방정식 등 추가 관계식이 요구됩니다. 부정정보 문제의 예시는 다음과 같습니다.
2차원 평형방정식에서 얻을 수 있는 식은 ΣFx = 0, ΣFy = 0, ΣM = 0 총 세 개인데 그림 (a)에 나타난 반력요소는 그보다 많은 4개이기 때문에 추가적인 관계식이 필요합니다.

아래 그림의 경우 총 여섯 개의 반력이 발생합니다.

Analysis by Deflection Curve
이러한 부정정보 문제는 보의 처짐 곡선을 구하는 것으로 해결할 수 있습니다.
일반기계기사 등 자격증 시험에서는 이 다음에 소개할 중첩법이라는 빠른 방법을 사용하지만 기본적으로 처짐곡선으로 구할 수 있다는 것을 알아두는 것이 좋습니다.
다음과 같은 방법으로 부정정보 문제를 해결할 수 있습니다.
1. 모든 반력을 표시하고 여분력을 설정
2. 확정지어야 하는 미지수는 처짐곡선을 구할 때 나오는 적분상수와 미지반력(여분력)
* 여분력을 뭐로 정하느냐가 굉장히 중요합니다.
여분력은 미지반력 중 몇을 보에 가해진 외력으로 취급한것이며 경계조건을 잘 유도하는 것이 문제시간을 빠르게 단축할 수 있습니다.
(예제 1) 보에 작용하는 모든 반력을 구하여라

보에 작용하는 반력은 벽에 작용하는 모멘트와 수직, 수평 방향 반력과 롤러에서 작용하는 수직 방향 반력까지 총 4개입니다.
따라서 해당 문제는 부정정보 문제라는 것을 알 수 있습니다.
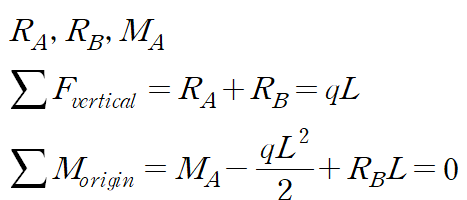
A점에서 수평방향 반력은 무시하겠습니다.
여분력을 어떻게 설정하든 상관없지만 오른쪽 롤러의 반력을 여분력으로 설정하면 단순한 외팔보 문제가 됩니다.

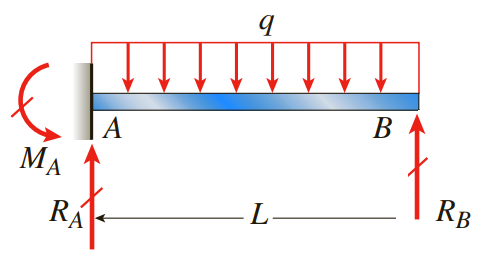
이를 토대로 처짐곡선을 구합니다. 처짐곡선을 구하는 방법은 아래 게시글 참조 바랍니다.
https://subprofessor.tistory.com/169
[재료과학] 보의 처짐 예제
#재료과학 목차 1. 처짐 미분방정식 2. 예제 풀이 보의 처짐 문제는 기본적으로 미분방정식으로부터 파생되는 적분상수들을 처리해줌으로 해결할 수 있습니다. 그 과정에서
subprofessor.tistory.com

이후로는 일반적인 처짐곡선 구하는 문제처럼 풀면 됩니다.

미지수는 C1, C0, RB 총 세 개입니다.
문제의 경계조건에서 양끝단에서 처짐양이 0이라는 것과 왼쪽에서 처짐각이 0이라는 것까지 총 세 개의 관계식을 유도합니다.



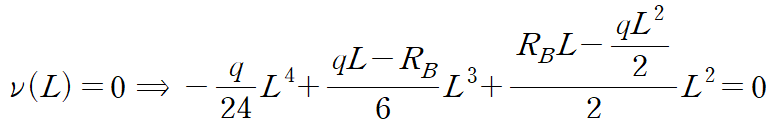
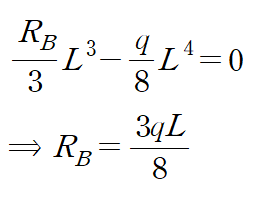
이것을 이용해 나머지 반력을 구합니다.

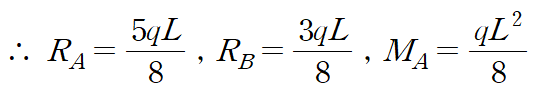
Method of Superposition
부정정보 문제를 풀 때마다 처짐곡선을 새로 구해 미지반력을 결정하는 것은 매우 시간이 오래 걸리기 때문에, 기본 케이스들을 활용하는 "중첩법"으로 풀이과정과 시간을 대폭 줄일 수 있습니다.
1. 평형방정식을 세우고 여분력을 선택
2. 원래 하중과 여분력을 분리하여 각각 별개의 구조물에 작용한다고 가정
3. 각각의 하중시스템의 처짐을 테이블로부터 구한 후 중첩
4. 기하학적 조건을 고려해 적합방정식을 세운다(δ=0, θ=0)
5. 평형방정식과 적합방정식으로부터 반력을 결정
처짐 테이블은 아래와 같이 주어집니다.(출처 : mechanics of material, Barry J. Goodno & James M. Gere, 9th edition)


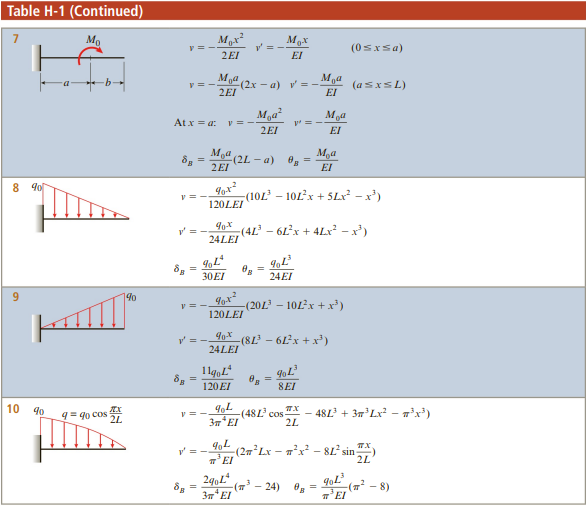



앞선 예제를 중첩법으로 풀어보겠습니다.
(예제 2) 보에 작용하는 모든 반력을 구하여라

마찬가지로 평형방정식을 세우고 여분력을 설정합니다.

이때 여분력은 보의 형태가 테이블에서 찾을 수 있는 형태가 되게끔 설정합니다.
RB를 여분력으로 잡으면 외팔보로 취급 가능하며 위 테이블에서 H-1-1, H-1-4를 사용할 수 있습니다.

부정정보에는 분포하중 q와 하중 RB가 가해진다고 볼 수 있으며 이를 분리하면 다음과 같습니다.
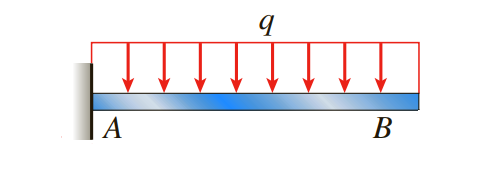

분포하중 q에 의한 B점에서의 처짐과 처짐각은 다음과 같습니다.

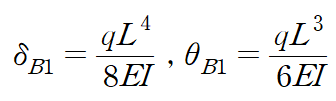
집중하중 RB에 의한 처짐과 처짐각은 다음과 같습니다.


이때 집중하중의 방향이 테이블과 반대이기 때문에 처짐과 처짐각이 반대방향이라는 것을 염두하고 있어야 합니다.
처음 제시된 부정정보에서 B점의 지지가 롤러였기 때문에 처짐각은 알 수 없으나 처짐량이 0이라는 조건을 유도할 수 있습니다.
이것은 분포하중에 의한 처짐과 집중하중에 의한 처짐을 모두 더했을 때 0이어야 한다는 것을 의미합니다.

이를 평형방정식에 적용하면 나머지 반력도 구할 수 있습니다.
※ 미지반력은 4개(수평반력 포함), 평형방정식은 3개(수평방향 힘의 평형방정식 포함)이므로 필요한 추가 관계식은 1개입니다. 이것을 처짐량이 같다는 적합방정식으로부터 유도하였습니다.
(예제 3) A점과 B점에서의 반력을 구하여라
q = 1 kN/m

반력은 A점에서 2개(수직반력, 모멘트 반력), B점에서 2개(수직반력, 모멘트 반력), 합해서 4개이며 유도할 수 있는 방정식은 수평방향 힘의 평형 방정식을 제외한 2개입니다.
B에서 발생하는 두 개의 반력을 여분력으로 잡고 중첩법을 이용해 적합방정식을 세운다면 B에서의 처짐량과 처짐각이 0이라는 2개의 관계식을 추가로 유도할 수 있습니다.

1. 평형방정식을 세우고 여분력을 정합니다.


여분력을 RB과 MB로 잡았습니다.
2. 부정정보에 작용하는 외력은 분포하중q, 집중하중 RB, 모멘트 B 입니다.
각각에 의한 처짐과 처짐각을 구합니다.
H-1-2, H-1-4, H-1-6 을 사용합니다.





3. 처짐량과 처짐각이 모두 0이라는 것을 사용합니다.
집중하중 RB에 의한 처짐의 부호만 반대이므로 아래 적합방정식을 얻습니다.


연립방정식을 풀면 다음과 같이 미지반력을 구할 수 있습니다.


'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 맥스웰 관계식 (Maxwell Relations) (0) | 2023.03.10 |
|---|---|
| [유체역학] 버킹엄 파이 정리, 반복변수법 (0) | 2023.02.26 |
| [재료역학] 용기 내 압력에 의한 응력 (0) | 2023.02.24 |
| [재료과학] 보의 처짐 예제 (1) | 2023.02.24 |
| [재료역학] 보의 처짐 : 처짐 미분방정식 유도 (Deflections of Beams) (0) | 2023.01.01 |