#재료과학
목차
1. 처짐 미분방정식
2. 예제 풀이
보의 처짐 문제는 기본적으로 미분방정식으로부터 파생되는 적분상수들을 처리해줌으로 해결할 수 있습니다.
그 과정에서 제약조건들로부터 적분상수의 개수만큼 관계식을 이끌어 내는 것이 관건입니다.
1. 처짐 미분방정식

최종적으로 얻고자 하는 건 처짐을 나타내는 처짐곡선 v입니다.
처짐 문제를 푸는 방법은 다음과 같습니다.
1. SFD -> BMD 구하기(x에 대한 식으로 나타내기)
2. 적분해서 처짐곡선 구하기
3. 적절한 관계식 찾아서 적분상수 처리하기
하나의 문제에 대해 위 세 가지 미분방정식을 사용해 처짐곡선을 구해보고
그 다음 다양한 예제를 2계 미분방정식으로 해결해보겠습니다.
2. 예제
(예제 1) 분포하중 q = 2kN/m 이고 보의 길이 L = 6m 일 때 보의 처짐곡선을 구하여라
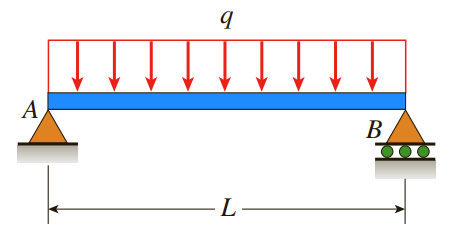
자중에 대한 내용이 없으면 굳이 고려하지 않습니다.
굽힘모멘트, 전단력, 분포하중 세 가지로 처짐곡선을 구해봅시다.
1. 굽힘모멘트 방정식

임의의 점에서의 굽힘모멘트를 구하면 처짐곡선을 구할 수 있습니다.
본 예제의 굽힘모멘트 선도(BMD)를 구하면 다음과 같습니다.
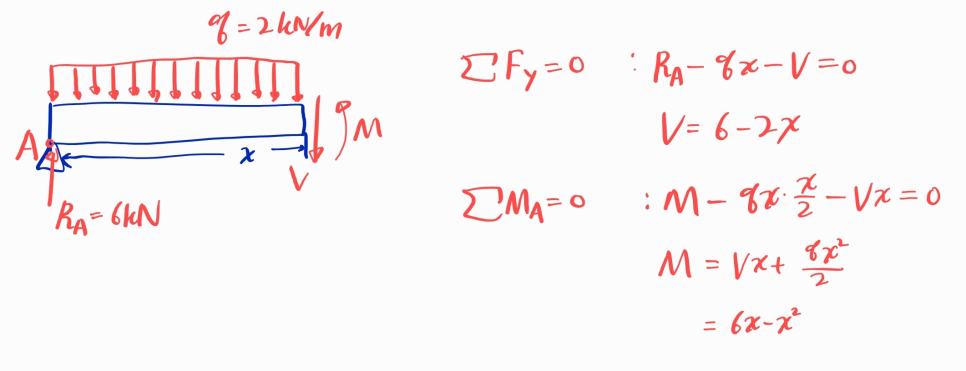
※ 전단력선도에서 왼쪽을 기준으로 잡으면 V는 아래방향, M은 반시계방향
전 구간의 전단력과 굽힘모멘트를 구했습니다.

처짐방정식에 M을 대입합니다.
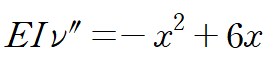
양변을 x에 대해 두 번 적분합니다.
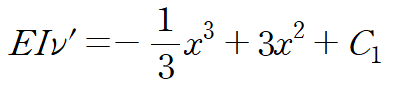
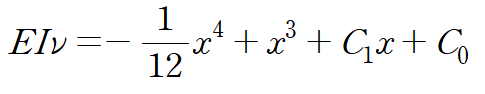
두 개의 미지수가 있고 해당 문제의 경계조건은 보의 양단의 처짐이 0이라는 것입니다.(지지점에서는 처짐 발생 X)
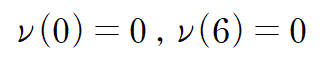

따라서 보의 처짐곡선은 다음과 같습니다.
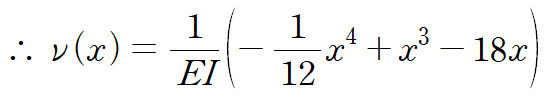
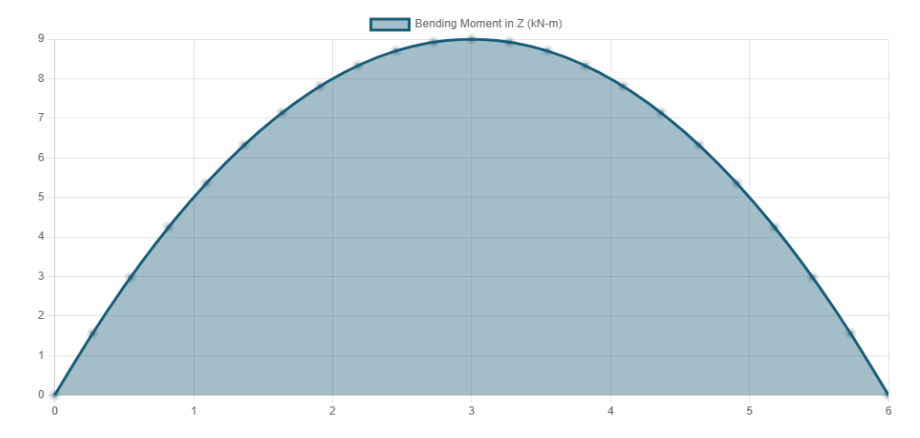
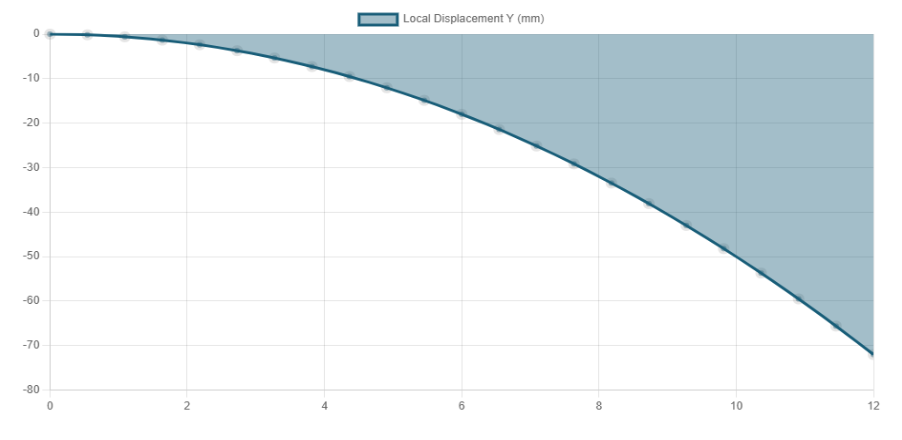
처짐곡선은 보가 쳐졌을 때의 모양을 의미합니다.
아래 그림은 특정 E, I에 대한 처짐곡선입니다.
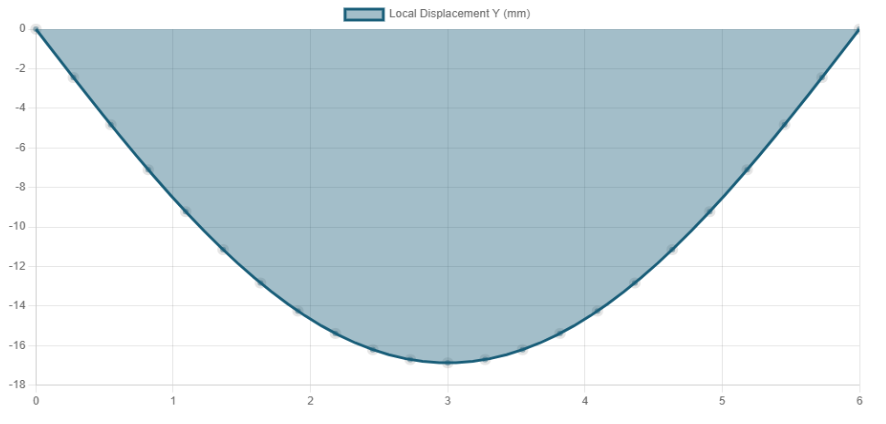
2. 전단력 방정식
아래 3계 미분방정식에
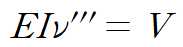
앞서 구한 전단력 V를 대입합니다.

마찬가지로 처짐곡선 v에 대한 식을 얻을 때까지 적분(세 번)합니다.
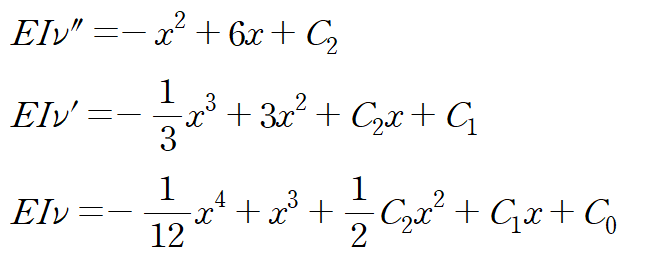
미지수가 세 개인데 표면적으로는 관계식이 경계조건 두 개 밖에 없어보입니다.

대칭성, 굽힘모멘트의 성질 등을 사용하면 추가 관계식을 이끌어낼 수 있습니다.
보가 중앙 x = 3 지점을 기준으로 대칭이니 중앙에서 보의 처짐각(v')이 0임을 사용할 수도 있고

양단에서 굽힘모멘트가 0임을 사용할 수도 있습니다.(본 예제의 경우만 해당. 캔틸레버(fixed support) 보나 양단에 굽힘모멘트가 작용하고 있는 경우는 제외)
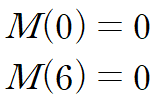
셋 중 어느 관계식을 사용하더라도 동일한 결과를 얻습니다. 저는 x = 0에서 굽힘모멘트가 0임을 사용하겠습니다.

2계 미분방정식을 풀었을 때와 동일한 결과를 얻었습니다.

3. 분포하중 방정식
분포하중 q를 사용하면 4계 미분방정식으로부터 4개의 상수가 나옵니다.
이에 따라 4개의 관계식을 이끌어 내야 하기 때문에 그다지 선호되는 방법은 아닙니다.
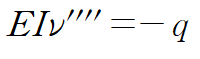
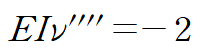
마찬가지로 4 번 적분해서 상수가 포함된 처짐곡선을 얻습니다.

아래 네 가지 관계식을 사용하겠습니다.

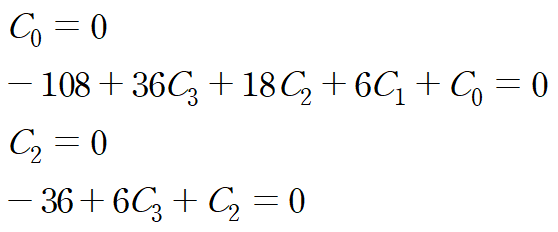
그냥 풀어도 되지만 미지수가 많이 떄문에 행렬로 가져와서 해를 구하겠습니다.
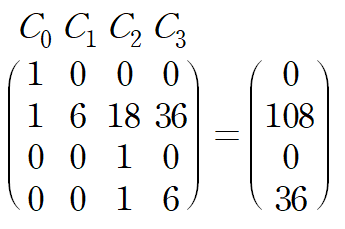
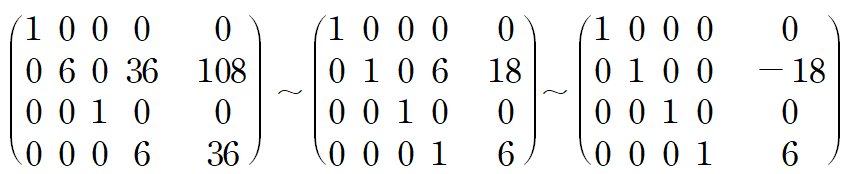

앞선 두 방법과 같은 처짐곡선을 얻을 수 있습니다.

(예제 2) 보의 처짐곡선을 구하여라
L = 12m, M = 2kN·m
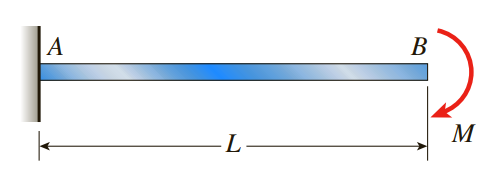
자중을 고려하지 않기 때문에 순수굽힘 문제로 해석할 수 있습니다.
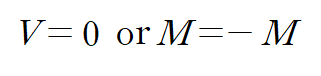
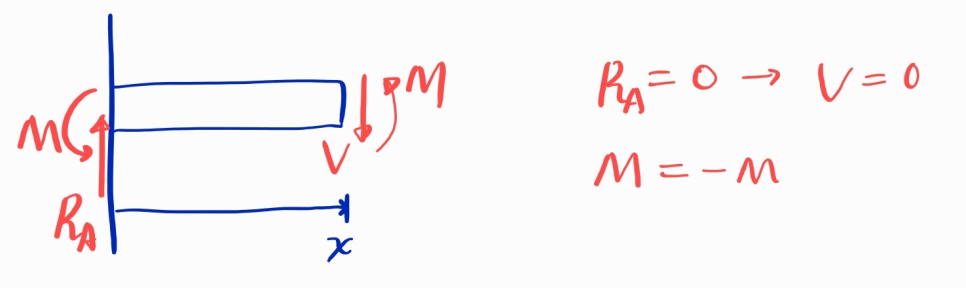
굽힘모멘트의 부호가 음인 것은 부호규약 때문입니다. 일반적으로 U자형으로 휘게 하는 모멘트를 양으로 약속합니다.
굽힘모멘트를 사용해 처집곡선을 구하겠습니다.
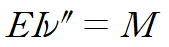
M = -2로부터 처짐곡선을 구합니다.
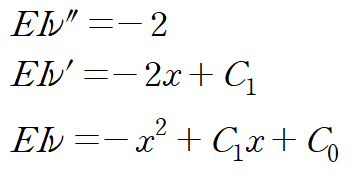
캔틸레버 보(외팔보)의 경우 고정된 지점의 처짐이 0이라는 것과 그 지점에서 처짐각이 0이라는 성질이 있습니다.
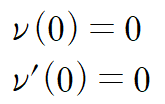

(예제 3) 보의 처짐곡선을 구하여라

SFD, BMD에 익숙하신 분들은 piecewise function 형태로 SFD와 BMD가 그려진다는 것을 직관적으로 알 수 있을텐데
이런 경우 함수 간의 경계에서 처짐과 처짐각이 동일하다는 것을 관계식으로 사용할 수 있습니다.
처짐방정식에 대입할 굽힘모멘트를 구합니다.
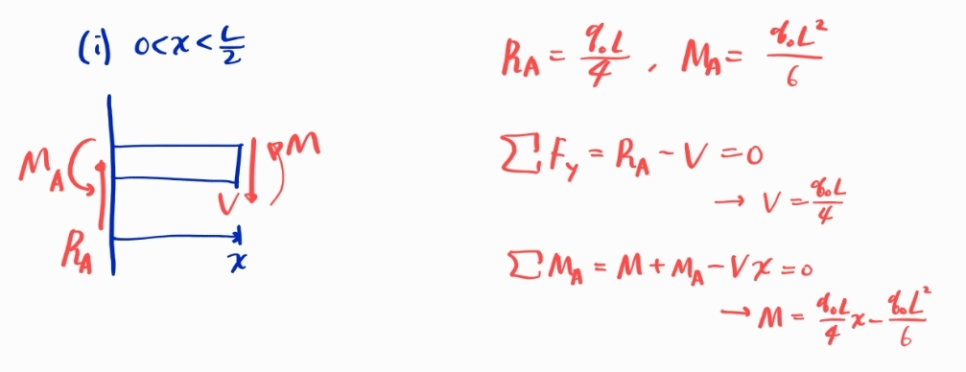

이상을 종합하면 아래와 같습니다.

각각 두 번 적분하면 네 개의 적분상수가 나옵니다.
처짐곡선은 연속이며 매끄러워야 하므로 아래와 같이 네 가지 관계식을 얻을 수 있습니다.
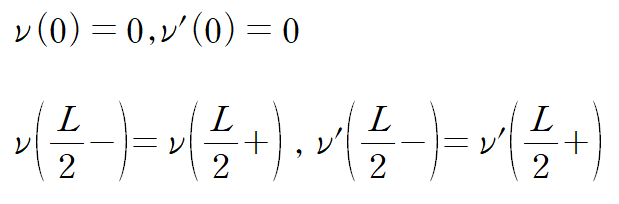
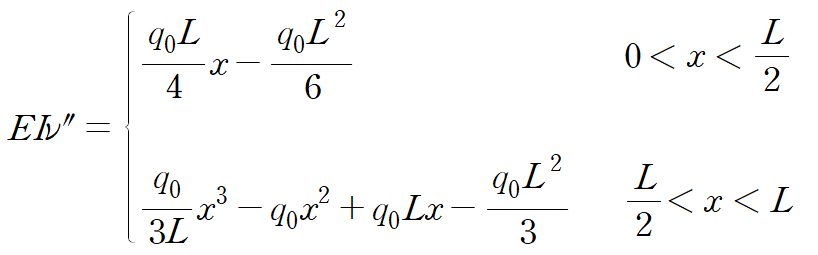


네 가지 관계식을 적용합니다.
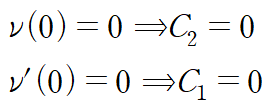
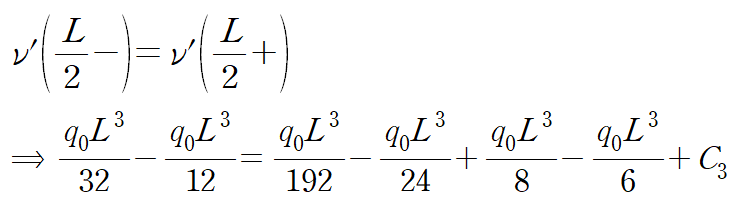
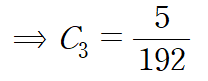
같은 방법으로 C4를 구할 수 있습니다.
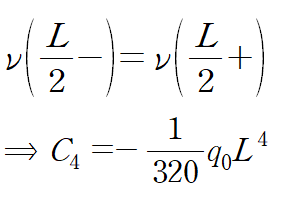
이상을 정리하면 다음과 같습니다.

'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 부정정보 예제 (3) | 2023.02.24 |
|---|---|
| [재료역학] 용기 내 압력에 의한 응력 (0) | 2023.02.24 |
| [재료역학] 보의 처짐 : 처짐 미분방정식 유도 (Deflections of Beams) (0) | 2023.01.01 |
| [재료역학] 보의 순수 굽힘 - 공식 편 (2) | 2022.12.31 |
| [재료역학] 보의 순수 굽힘 - 개념 편 (2) | 2022.12.26 |