#재료역학
순수 굽힘(Pure bending)이란 굽힘모멘트가 일정한, 즉 전단력이 작용하지 않는 굽힘을 뜻합니다.
지난 글에서 SFD, BMD를 그릴 때도 설명했지만 전단력은
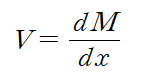
로 정의됩니다.
굽힘모멘트가 일정하다면 dM/dx가 0이 되고, 따라서 전단력 V=0이 됩니다.
이번 글에서는 중립면, 중립축, 보의 곡률과 같은 순수 굽힘 개념들에 대해 알아봅시다. 그 후에 추가적인 식 유도와 예제 풀이를 통해 익숙해지자구요

1. Definition
(1) 직교 축

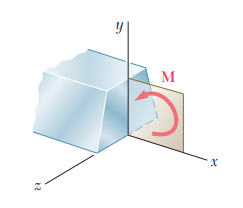
위 그림은 굽힘이 일어나는 보에 대해 x, y, z 축을 설정한 것입니다. 보의 축 방향이 x축이 되고, 옆에서 바라보았을 때 위로 올라가는 수직 방향(vertical)이 y축으로 설정됩니다. x, y 축이 설정되었으면 오른손 법칙에 의해 z축이 자연스럽게 수립되지만, 보다 쉽게 설명하자면 위 그림 (a)을 보고 있는 방향으로 즉, 종이를 뚫고 '나오는' 방향이 z축으로 설정됩니다.
(2) 중립면

순수 굽힘이 일어나는 보에 대해 x축 방향 변형률 εx와 x축 방향 응력σx이 0인 면이 존재합니다.
위 그림에서 보가 U자를 그리며 휘어질 때, y축 방향으로 위쪽면 AB에는 압축(compress)이, 아래쪽면 A'B'에는 인장(tension)이 일어납니다. 마치 아래 그림처럼 말이죠
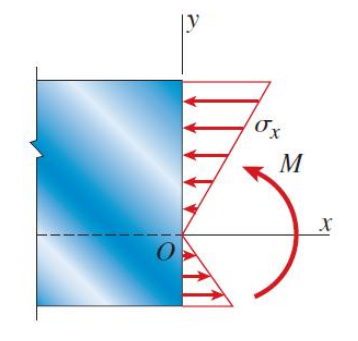
그림은 축에 수직인 단면을 잘랐을 때 x방향 응력을 나타낸 것입니다. 굽힘모멘트 M에 대해 위쪽면에는 압축응력, 아래쪽면에는 인장응력이 발생합니다. 압축도, 인장도 일어나지 않는 zx 면이 존재할 텐데, 그 면을 바로 중립면(Neutral surface)이라고 합니다. 길이가 변하지도 않고, 응력이 발생하지도 않는 면이라서 중립면이라는 이름이 붙여졌습니다.
추가적으로 중립면이 neutral plane이 아니라 neutral surface인 이유는 다름아닌 중립면이 곡면이기 때문입니다.
(3) 중립축
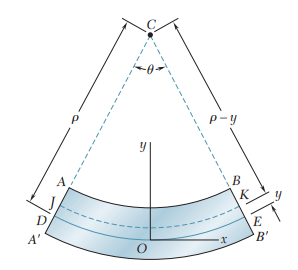
위 그림처럼 짧은 보를 생각해봅시다. 보를 U자로 휘게하는 순수 굽힘이 보에 발생하였습니다. 이때, 중립면은 면 DE입니다. 중립면 위의 어떤 점 O를 잡았을 때, 그 점을 기준으로 보의 굽힘이 대칭성을 가진다면, 그 점을 지나는 z축을 바로 중립축(Neutral axis)이라 합니다. 또한 일반적으로 중립축 위의 점 O를 기준으로 x, y, z 축을 잡습니다.
균일단면보라는 가정하에, 중립축의 위치는 보의 단면적에 대한 도심의 위치와 같습니다.
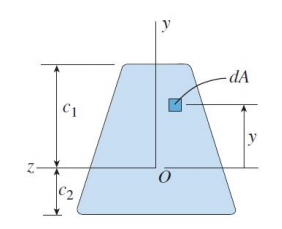
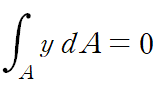
중립축의 위치가 왜 도심의 위치와 동일한지는 다음에 기회가 나면 알아보도록 하고, 중립축을 이렇게 구할 수 있구나 정도만 알고 넘어갑시다.
(4) 보의 곡률
순수 굽힘이 발생하면 보는 일종의 호(arc) 형태로 휘어집니다. 이 호의 중심을 곡률 중심(Center of curvature)이라고 하고, 곡률 중심으로부터 중립면까지의 거리를 곡률 반경(Radius of curvature) 또는 곡률 반지름이라 합니다. 곡률 중심은 C 또는 O'로 표시하고 곡률 반경은 보통 ρ로 표기합니다.
보의 곡률(Curvature)은 다음과 같이 곡률 반경의 역수로 정의됩니다.

이때 곡률의 부호 규약은 다음 그림과 같습니다.

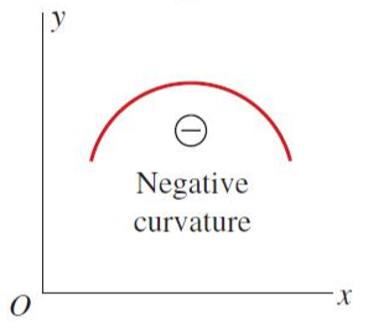
U자형으로 보가 휘게 되어 호(Arc)의 중심이 보 위쪽에 위치할 때가 양의 곡률(Positive curvature)입니다.
※곡률은 k가 아니라 [kappa]라고 읽습니다.
(5) 굽힘 강도
굽힘 강도(Bending strength)는 재료의 탄성계수 E와 단면 2차 모멘트 I로 정의됩니다.

여기서 단면이라 함은 축방향에 수직인 단면을 말합니다. 균일 단면보의 경우 이 I의 값이 일정하겠지요
여기까지 순수 굽힘 - 개념편 이었습니다. 다음 시간에는 보의 순수 굽힘 해석에 있어서 필요한 식들을 정리해보도록 합시다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 보의 처짐 : 처짐 미분방정식 유도 (Deflections of Beams) (0) | 2023.01.01 |
|---|---|
| [재료역학] 보의 순수 굽힘 - 공식 편 (2) | 2022.12.31 |
| [재료역학] 전단력 선도, 굽힘모멘트 선도 예제 (SFD, BMD) (0) | 2022.12.26 |
| [동역학] 상태공간 모델(State-space model), 전달함수(Transfer Function) (0) | 2022.12.15 |
| [동역학] 전달함수(Transfer Function) 정의, 연립 운동방정식 예제 (0) | 2022.10.26 |