0. Introduction
1.경계층(Boundary Layer)
경계층(Boundary Layer)을 분석하는 것은 점성력이 지배적인 유동 영역과 그로 인한 손실(에너지, 운동량 등)을 계산하기 위함입니다.
경계층은 "유동속도가 Free stream velocity의 0.99배인 지점"으로 정의됩니다.
벽면에서 유동속도를 0이라 두면(경계조건) 벽면부터 경계층까지는 점차 속도가 증가하게 됩니다.
이때 "경계층 밖에서는 점성에 의한 효과를 무시할 수 있다"라는 해석이 가능해지는 것입니다.
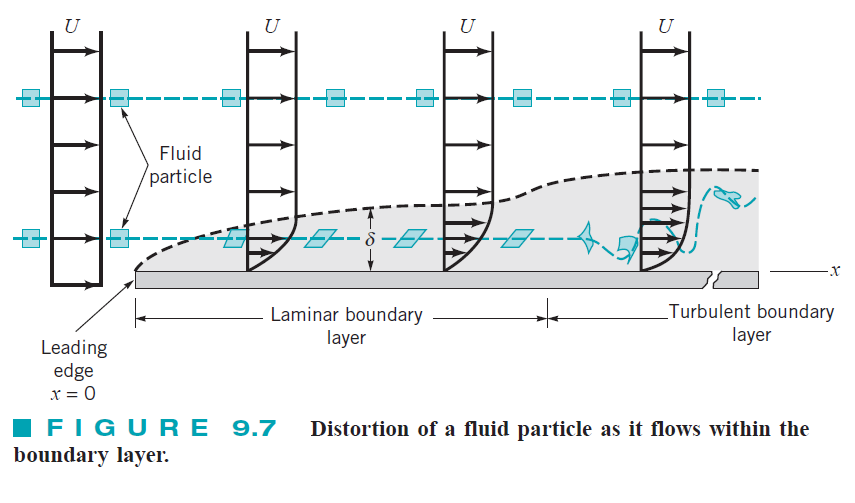
경계층은 물체를 따라 유동하며 점점 성장하게 됩니다.
초기에는 층류 경계층으로 성장하다가 천이구간(Transition)을 지나 난류 경계층으로 성장하게 됩니다.
2. 배제 두께(Boundary layer displacement thickness; displacement thickness)
아래 그림은 경계층 δ 와 배제 두께 δ* 의 정의를 나타낸 그림입니다.
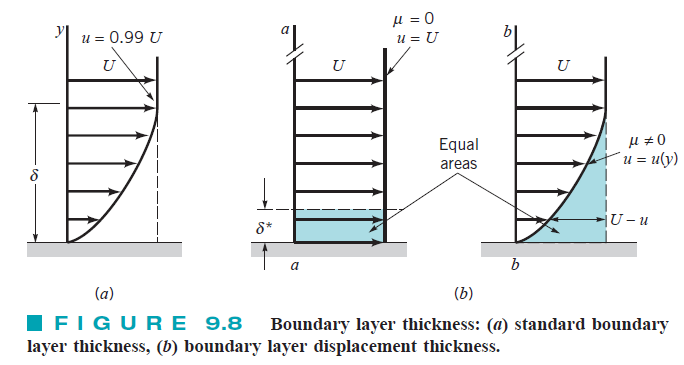
점성 효과로 인해 경계층 내부에서는 점성이 없었을 때 기대되는 유체의 유량에 손실이 일어나게 됩니다.
이 손실된 유량을 나타내는 것이 바로 배제 두께입니다.
유량을 통한 배제 두께의 수학적 정의는 다음과 같습니다. (Q = Av 사용한 것)
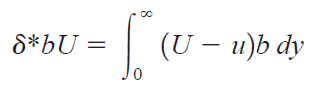
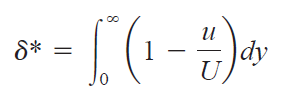
3. 운동량 두께(Momentum Thickness)
운동량 두께란 경계층 내부의 점성 효과로 인해 손실된 운동량을 의미합니다.(deficit in momentum flux)
이러한 정의로부터 다음과 같은 적분 표현을 가집니다.
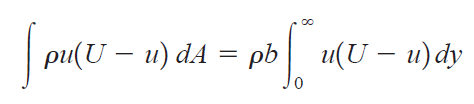
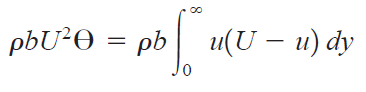
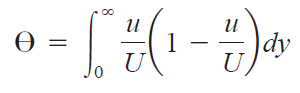
경계층을 분석하는 것이 중요한 이유는 앞서 말했듯이 점성 효과를 분석하기 위함인데 이것은 점성으로 인한 Drag를 의미하기도 합니다.
경계층을 계산하기 위한 대표적인 방법으로는 Prandtl/Blasius의 경계층 분석(층류만 가능) 과 오늘 소개하는 운동량 적분 방정식이 있습니다.
1. Momentum Integral Equation
Momentum Integral Equation, Karman Integral Equation(von karman이 1921년에 이 방정식을 유도) 라 불리는 운동량 적분 방정식이란 경계층 이론의 주요 요소인 배제 두께와 운동량 두께로부터 벽면에 작용하는 전단응력을 구하는 방정식입니다.
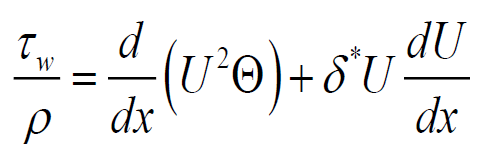
순서대로 τw는 wall shear stress, ρ는 유체의 밀도, U는 free stream velocity(또는 U∞), Θ는 momentum thickness, δ*는 displacement thickness 입니다.
운동량 적분 방정식이 가지는 의미는 다음과 같습니다.
1. 벽면 전단응력(Wall shear stress)으로부터 항력(Drag)을 계산할 수 있기에 운동량 적분 방정식을 사용하는 것이다.
2. 배제 두께와 운동량 두께는 적절한 velocity profile을 가정함으로 구할 수 있다.
3. 운동량 적분 방정식은 Prandtl/Blasius solution과 달리 층류/난류 모두 유효하다.
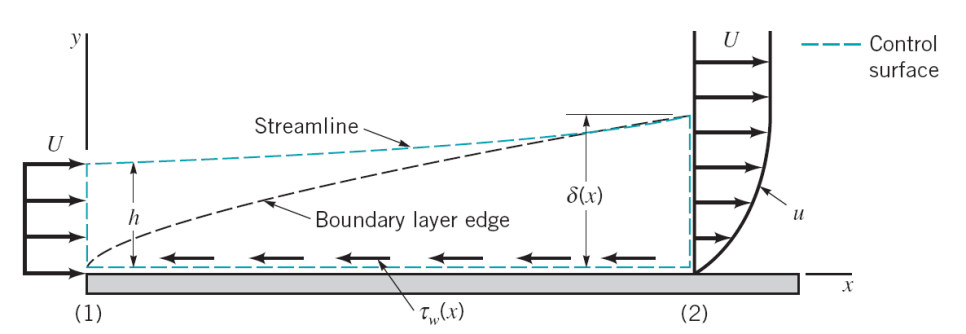
유도과정이 길고 각 단계마다 다양한 개념적 이해가 요구됩니다.
(0) 연속방정식과 x방향 나비에-스톡스 방정식부터 시작
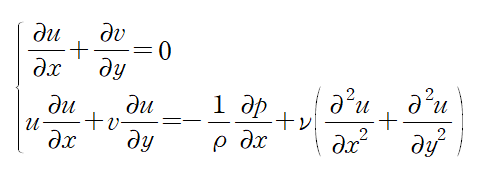
(1) 나비에-스톡스 방정식의 우변에서 베르누이 방정식을 적용
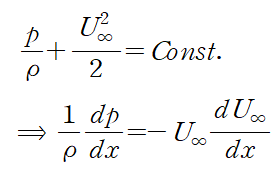
이때 U∞는 경계층 외부에서의 x방향 속도를, u는 경계층 내부를 포함하는 유체의 x방향 속도를 의미합니다.
또한 경계층 내부에서 유체의 속도가 y방향으로 변하는 정도가 x방향으로 변하는 것보다 훨씬 크다고 생각합니다.
즉 우변의 x방향 점성항을 무시할 수 있다는 것입니다.
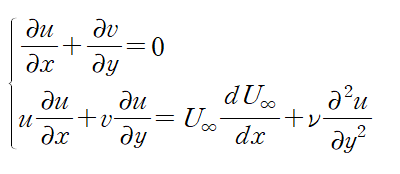
이 두 가지 가정은 모두 Scale Analysis로부터 기인한 것이지만 여기서는 생략하겠습니다.
(2) 연속방정식의 양변에 u를 곱하고 나비에 스톡스 방정식과 더합니다.
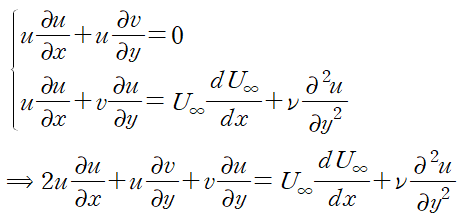
더하고 나면 좌변이 다음과 같이 정리됩니다.
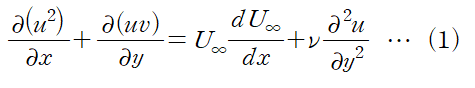
(3) 식 (1)의 양변을 y에 대해 적분합니다.
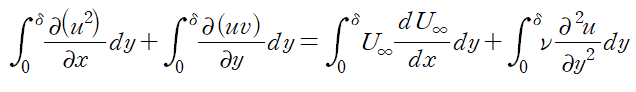
각각의 항을 살펴보겠습니다.
좌변의 첫째항은 아직은 손댈 수 없으니 일단 그대로 놔둡니다.
두 번째 항은 다음과 같이 적분됩니다.
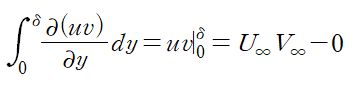
U∞, V∞은 각각 경계층 외부에서의 x, y방향 속도입니다.
벽면에서(y = 0) 유체가 정지해있기 때문에 U = 0 이므로 uv(0) = 0입니다.
우변의 첫째항도 마찬가지로 놔두고 두 번째 항은 보겠습니다.
유체의 작용하는 전단응력의 정의에 의해 두 번째 항이 정리됩니다.
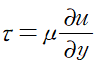
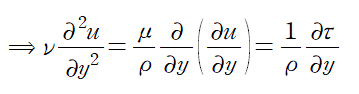
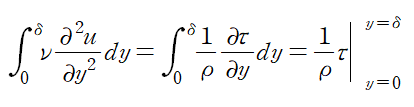
경계층에서 유체가 본래 유동속도를 회복하므로 경계층에서 전단응력은 0이고 벽면에서 전단응력을 wall shear stress라 하므로
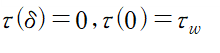
다음과 같이 식이 정리됩니다.
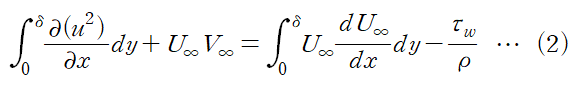
(4) 연속방정식의 양변을 y에 대해 적분함으로 V∞을 소거합니다.
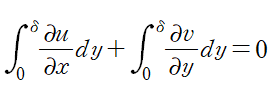
좌변의 두 번째 항이 다음과 같이 정리됩니다.
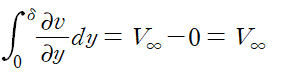
따라서 V∞은 다음과 같습니다.
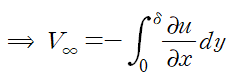
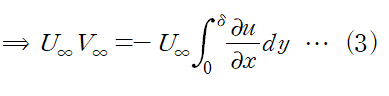
또한 아래와 같은 관계식이 성립하므로(곱의 미분법)
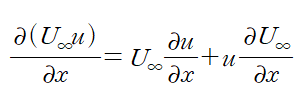
식 (3)은 두 개의 적분식으로 분해됩니다.
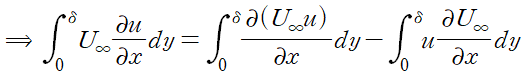
여기서 U∞(free stream velocity)가 y좌표와 관계가 없기 때문에 적분기호 넣어 정리해주었습니다.
따라서 U∞V∞ 항은 다음과 같이 정리됩니다.
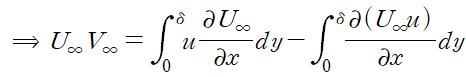
이것을 식 (2)에 대입합니다.
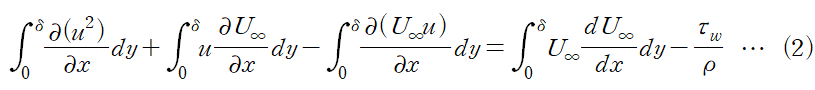
(5) 식 (2)의 양변을 정리합니다.
네 개의 적분식을 한 쪽으로 몰겠습니다.
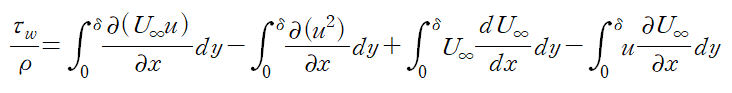
(6) 우변에 위치한 네 개의 적분식을 묶어 정리합니다.
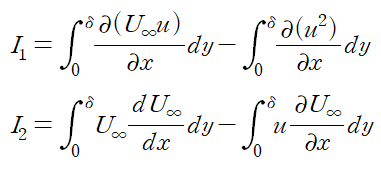
먼저, I1을 보면 편미분 기호로 묶을 수 있습니다.
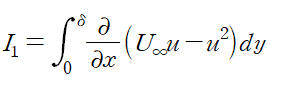
편미분되는 함수를 다음과 같이 표현한다면
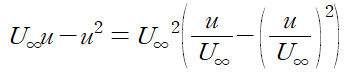
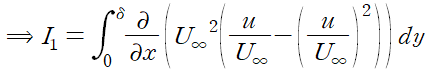
Leibniz integral rule에 의해 편미분 기호가 적분기호 밖으로 빠져나올 수 있습니다.
Leibniz integral rule - Wikipedia
From Wikipedia, the free encyclopedia Differentiation under the integral sign formula This article is about the integral rule. For the convergence test for alternating series, see Alternating series test. In calculus, the Leibniz integral rule for differen
en.wikipedia.org
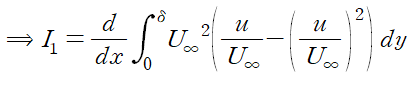
이때 U∞(free stream velocity)는 y와 무관하므로 적분기호 밖으로 빠져나올 수 있습니다.
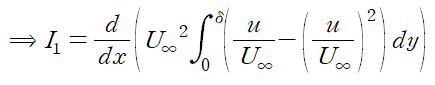
이렇게 정리하고 나니까 운동량 두께가 보입니다.
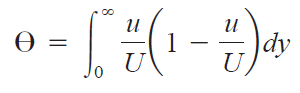
따라서 I1는 아래와 같이 간단하게 정리됩니다.
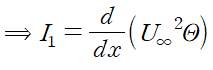
I2 또한 마찬가지로 피적분함수를 적절히 손보아 정리할 수 있습니다.
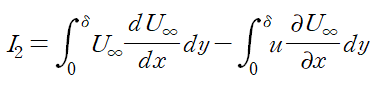
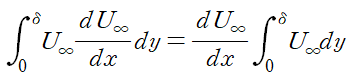
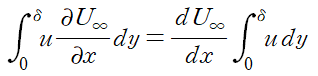
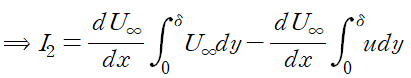
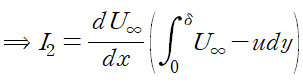
앞서 I1에서 운동량 두께를 유도했듯이 배제 두께를 대입할 수 있도록 피적분함수를 정리합니다.
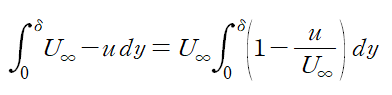
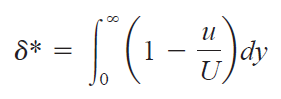
이것을 대입해 정리합니다.
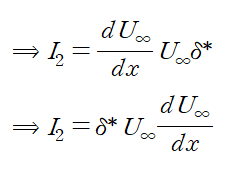
여기까지의 과정을 종합하면 다음과 같이 운동량 적분방정식이 완성됩니다.
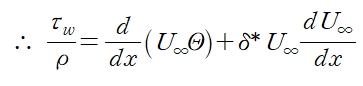
운동량 적분방정식을 통해 경계층과 항력을 구하는 활용 과정은 다음 게시글에서 다뤄보겠습니다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 블라시우스 해법(Blasius Solution) 유도 (0) | 2024.06.13 |
|---|---|
| [재료역학] 모어 원 그리는 법(Morh's Circle) (0) | 2024.06.12 |
| [유체역학] 항력계수(Drag Coefficient) (0) | 2023.08.09 |
| [유체역학] 수력도약(Hydraulic Jump) (1) | 2023.08.05 |
| [재료과학] 재휘현상(Recalescence) (0) | 2023.06.30 |