#열전달
유체역학에서 주요 관심사가 압력분포와 속도분포이듯 열전달에서의 주요 관심사는 온도분포(temperature distribution)와 열전달량(heat)입니다.
온도분포를 알게 되면 heat flux와 heat rate를 알 수 있기 때문인데 세 가지 열전달 모드(전도, 대류, 복사)에 대한 heat은 모두 temperature 로 기술되어 있습니다.

때문에 열전달에서 물어보는 것이 대부분 이 온도와 열전달량(heat flux, heat rate)에 초점이 맞춰질 수밖에 없습니다.
이런 이유로 우리도 문제를 대할 때 온도분포와 열전달량에 관심을 가지는 것이 자연스러운 수순입니다.
간단한 예제들로 전도 열전달, 온도분포, 열전달량에 익숙해져봅시다.
Example
(예제 1) 아래 그림과 같이 단열재가 설치되어 있다. 실내 온도는 섭씨 25도, 실외 온도는 영하 -10도 일 때, 단열재를 통과하는 열유속(heat flux)를 구하여라. 이때 L = 200mm 이고 단면에 수직한 열전달만을 고려한다.

고체를 지나가는 heat flux를 구하는 것이니, 이 문제는 열전달 세 가지 모드 중 전도에 관한 문제입니다.
전도 열전달 공식은 다음과 같습니다.

위 식에서 좌변이 heat flux고 우변의 k가 열 전도도(thermal conductivity)입니다.
또한 열이 흐르는 방향은 높은 온도에서 낮은 온도이므로 문제에 표시된 x축 방향(x = 0 to x = L)이 바로 heat 의 방향이 됩니다.
steady stete, 1D 가정을 적용하면 다음과 같이 heat flux를 구할 수 있습니다.

여기서 온도 분포를 단순히 선형 분포라 둔 이유는 확산방정식의 해로부터 얻어지는 결론이기 때문입니다.

1D의 경우 아래와 같이 정리되고

위 미분방정식의 해를 구하면 선형 프로파일을 얻습니다.

그렇기 때문에 전도 열전달에서 단순히 온도 차이를 길이로 나눈 것이 열전달량이 되는 것입니다.
(예제 2) 어떤 고체 물질의 내부 온도 분포가 다음과 같을 때, 각 위치에서 heat flux를 구하여라.
단 A, B, C는 상수

고체 물질 내부에 전도에 의한 열전달만이 존재한다고 가정합시다.
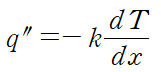
위 conduction heat flux 공식에 주어진 온도 분포를 넣어줍니다.

따라서 각 위치에서의 heat flux는 다음과 같습니다.

(예제 3) 아래 그림의 symmetric shape 에 대해 steady state, 1D heat conduction을 가정하자. 내부에 열 생성이 없을 때(no internal heat generation) 열 전도도(thermal conductivity) k(x)를 유도하여라.
단면적, 온도 분포, 열 전달량(heat rate)은 다음과 같다.


heat rate는 heat flux에 단면적을 곱한 것이므로 다음과 같은 관계식을 가집니다.

우리가 가진 관계식에서 구해야 하는 것은 k이고, 주어진 것은 A, T, q이므로 위 관계식에 대입하면 k를 구할 수 있겠네요.


따라서 열전도도는 다음과 같습니다.

'기계공학 > 열전달' 카테고리의 다른 글
| [열전달] 1D transient conduction(1) : Lumped Capacitance Method (1) | 2024.01.06 |
|---|---|
| [열전달] 1차원 전도 예제(with heat generation) (1) | 2023.11.16 |
| [열전달] 열전도 확산방정식 유도 (0) | 2023.11.05 |
| [열전달] Fin Analysis, General Equation (1) | 2023.10.05 |