#미분적분학
이 글에서 다루는 삼각함수 적분은 다음과 같습니다.
삼각함수의 거듭제곱과 곱해져있는 함수들의 적분을 다룹니다.
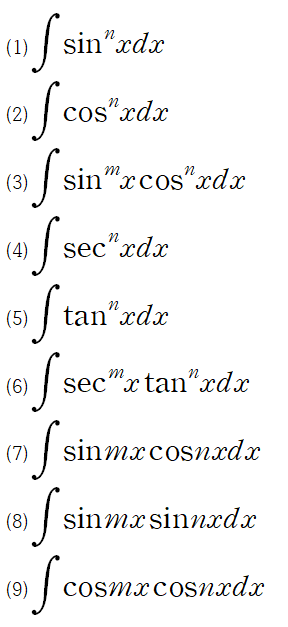
1. (sin x)^n, (cos x)^n

(1) n이 짝수인 경우
: 반각 공식을 사용해서 차수를 계속해서 내립니다.
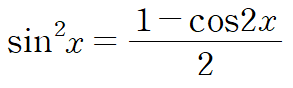
예시로 (sin x)^4 를 봅시다

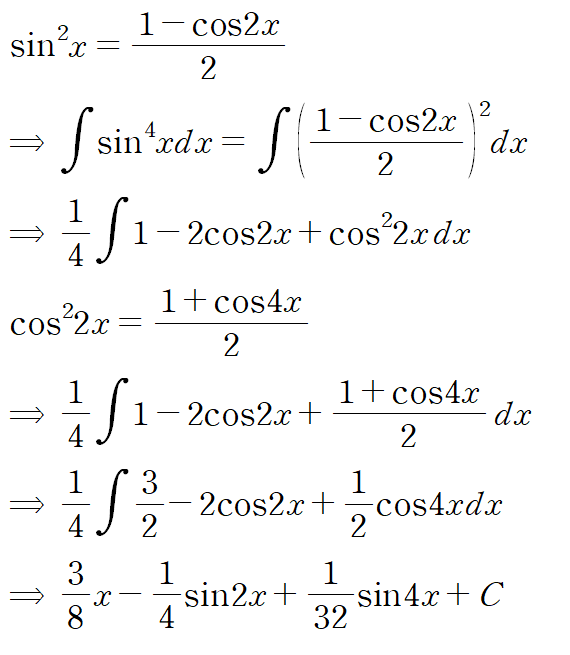
(sin x)^6도 마찬가지로 풀되, cos x 의 홀수 승의 적분에 대해서는 이 다음에 나오는 내용을 참고합시다.

(2) n이 홀수인 경우
: 하나만 남기고 나머지를 모두 바꾼 후(sin은 cos으로, cos은 sin으로) 치환적분을 사용합니다.
아래 삼각함수 성질을 이용합니다.
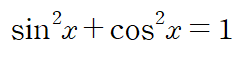
(cos x)^5을 예시로 보겠습니다.


2. (sin x)^m (cos x)^n

(1) 차수가 둘다 짝수인 경우
: 배각공식과 반각공식을 이용해 차수를 내립니다

예시로 (sin^4 x)(cos^2 x) 를 보겠습니다.
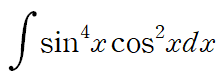


(2) 하나는 홀수, 하나는 짝수일 경우
: 기본적으로 홀수 차수인 것에서 하나만 남기고(치환적분을 위해) 나머지 부분은 때에 따라 배각, 반각을 사용하기도 하고 단순히 하나의 삼각함수로 바꾸어 치환적분을 수행할 수도 있습니다.
예시로 (sin^4 x)(cos^7 x)를 보겠습니다

(3) 둘 모두 홀수인 경우
: 먼저 낮은 차수로 묶고 배각 공식과 반각 공식을 사용해 차수를 내립니다.
예시로 (sin^3 x)(cos^5 x)를 보겠습니다.

3. (sec x)^n, (tan x)^n, (sec x)^m (tan x)^n

아래 삼각함수 성질을 사용해 sec x와 tan x 를 변환합니다.

또한 이 두 삼각함수를 적분하기 위해서는 sec x의 적분을 알 필요가 있습니다.

이것은 분모와 분자에 (sec x + tan x)를 곱하는 트릭입니다.
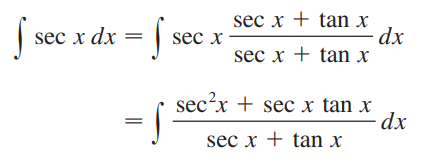
이후 분모를 치환하여 적분을 계산할 수 있습니다.

(1) sec x의 차수가 짝수인 경우
: (sec x)^2을 따로 뗴어놓고 나머지는 모두 tan x 로 바꿔 치환적분을 수행합니다.
예시로 (sec x)^4을 보겠습니다.
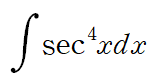

또다른 예시로 (sec x)^6 (tan x)^4 을 보겠습니다.

(2) (sec x)^n, 차수가 홀수인 경우
: 피적분함수가 sec x로만 이루어져있다면 부분적분과 같은 특수한 방법을 사용해야 합니다.

부분적분을 적용하고

우변을 정리합시다.

우변에 있는 (sec^3 x)의 적분을 좌변으로 넘기고 sec x 의 적분 공식을 사용하면 다음과 같습니다.

(3) (tan x)^n
: 차수가 짝수, 홀수 관계없이 (sec x)^2 를 떼어낸 후 tan x로 치환적분을 수행합니다.
예시로 (tan^7 x)을 보겠습니다.

먼저 tan^2 x를 떼어내 sec^2 x로 변환합니다.
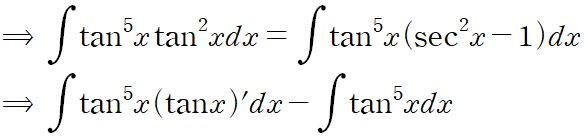
tan^5 x의 적분은 같은 방법으로 정리할 수 있습니다.
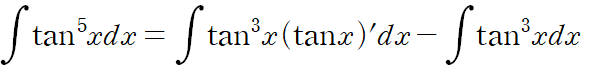
tan^3 x도 마찬가지입니다.
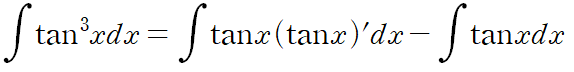
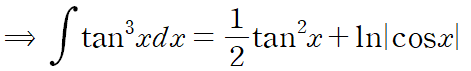
이것을 tan^5 x의 적분에 대입하여

tan^7 x을 얻을 수 있습니다.

(4) (sec x)^m (tan x)^n에서 tan x의 차수 n이 홀수인 경우
: (sec x tan x)을 떼어낸 후 sec x로 치환적분을 수행합니다.
예시로 (sec^4 x)(tan^3 x)을 보겠습니다.

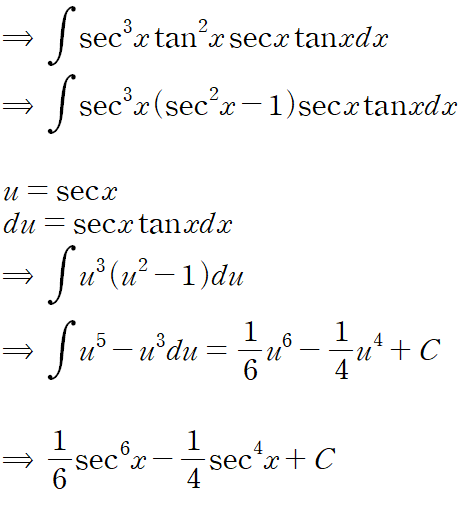
4. (sin mx)(cos nx), (sin mx)(sin nx), (cos mx)(cos nx)
다른 주기를 가지는 sin과 cos이 하나씩 곱해져있는 경우입니다.
이런 경우 삼각함수의 덧셈정리를 사용해 분리하는 것으로 적분을 수행합니다.
(1) (sin mx)(cos nx) 형태
: sin 덧셈정리를 사용해 분리할 수 있습니다.
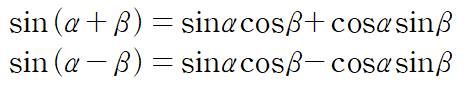
두 식을 더합니다.

이것이 의미하는 것은 다른 주기를 가지는 두 삼각함수의 곱을 합 또는 차 형태로 분리할 수 있다는 것입니다.

예시로 (sin 7x)(cos 2x) 를 보겠습니다.

공식을 바로 사용해도 되지만 원리를 적용해 풀어보겠습니다.

두 식을 더하거나 빼서 우리가 원하는 sin7x cos2x만 남길 수 있습니다. 여기서는 더해줘야겠지요

이로써 곱의 형태였던 피적분함수가 분리되고
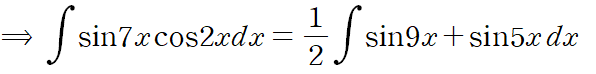
적분을 수행하면 아래와 같은 결과를 얻습니다.
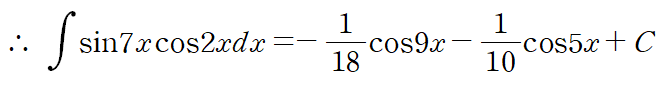
(2) (sin mx)(sin nx) 형태
: cos 덧셈정리를 사용해 분리할 수 있습니다.
sin sin이 등장하는 덧셈정리는 cos 덧셈정리입니다.
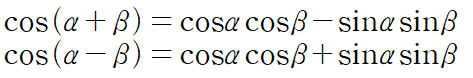
여기서 sin만 남기려면 두 식을 빼주면 되겠죠


예시로 (sin 7x)(sin 2x) 를 보겠습니다.
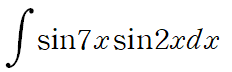
앞서 얻은 결과를 바탕으로 삼각함수를 분리하고 적분합니다.
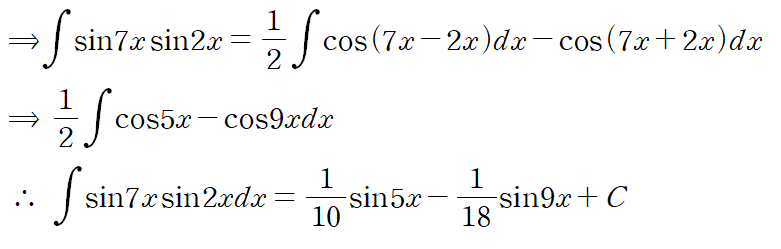
(3) (cos mx)(cos nx) 형태
: cos 덧셈정리를 사용해 분리할 수 있습니다.
마찬가지로 cos 덧셈정리를 사용합니다.
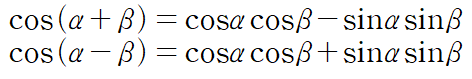
위 식에서 우변에 cos a cos b만을 남기기 위해서는 두 식을 더해주면 되겠죠
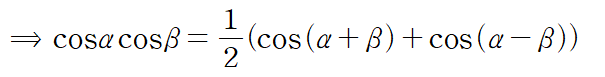
예시로 (cos 3x)(cos 4x) 를 보겠습니다.

앞서 얻은 결과를 바탕으로 삼각함수를 분리하고 적분합니다.
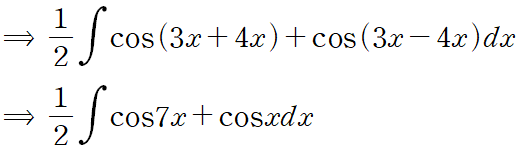
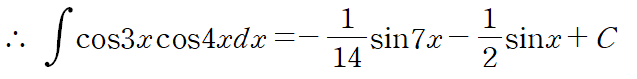
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| 미분적분학 멱급수와 수렴반경 쉽게 이해하기 - Power Series, Radius of Convergence (1) | 2024.10.21 |
|---|---|
| [미분적분학] 회전체 부피 구하기 : 디스크, 원통셸 방법 (4) | 2023.01.10 |
| [미분적분학] 방향도함수 (Directional Derivative) (0) | 2022.07.28 |
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.23 |
| [미분적분학] 라그랑주 승수법 예제 (0) | 2021.12.12 |