Fin Analysis
고체 표면에서는 주변 대기와 열교환이 일어나는데 이것을 대류(convection)라 합니다.
뉴턴의 냉각법칙에서 기인한 대류 열전달 관계식은 다음과 같습니다.(cooling, Ts > T∞ )
대류 열전달 관계식을 구성하는 인자로는 h(열전달 계수; heat transfer coefficient), A(표면의 면적), Ts(표면 온도), T∞(대기 온도, 보통 상수로 가정)가 있습니다. 좌변의 q는 heat rate [W] 입니다.
어떤 물체에서 열이 많이 발생되어 빠르게 식혀야 하는 상황을 생각해보면 이 heat rate가 높을수록 빠르게 열을 바깥으로 내보낼 수 있으니 열전달 계수 h를 높이거나 전열면적 A를 높이거나 표면과 대기의 온도차를 높이는 세 가지 방법을 생각해볼 수 있습니다.
fin analysis란 이러한 heat rate를 높이기 위해 대기와 맞닿는 면적(전열면적; 열교환이 일어나는 면적을 의미함) A를 높이기 위한 연구입니다. 확장된 surface를 부착하는 방법인데 이 extended surface를 fin이라 부릅니다.

이러한 fin의 예시로는 회로에서 발생되는 열을 빠르게 방출하기 위해 열전도가 우수한 금속(high k)으로 구성된 기판이 있습니다.
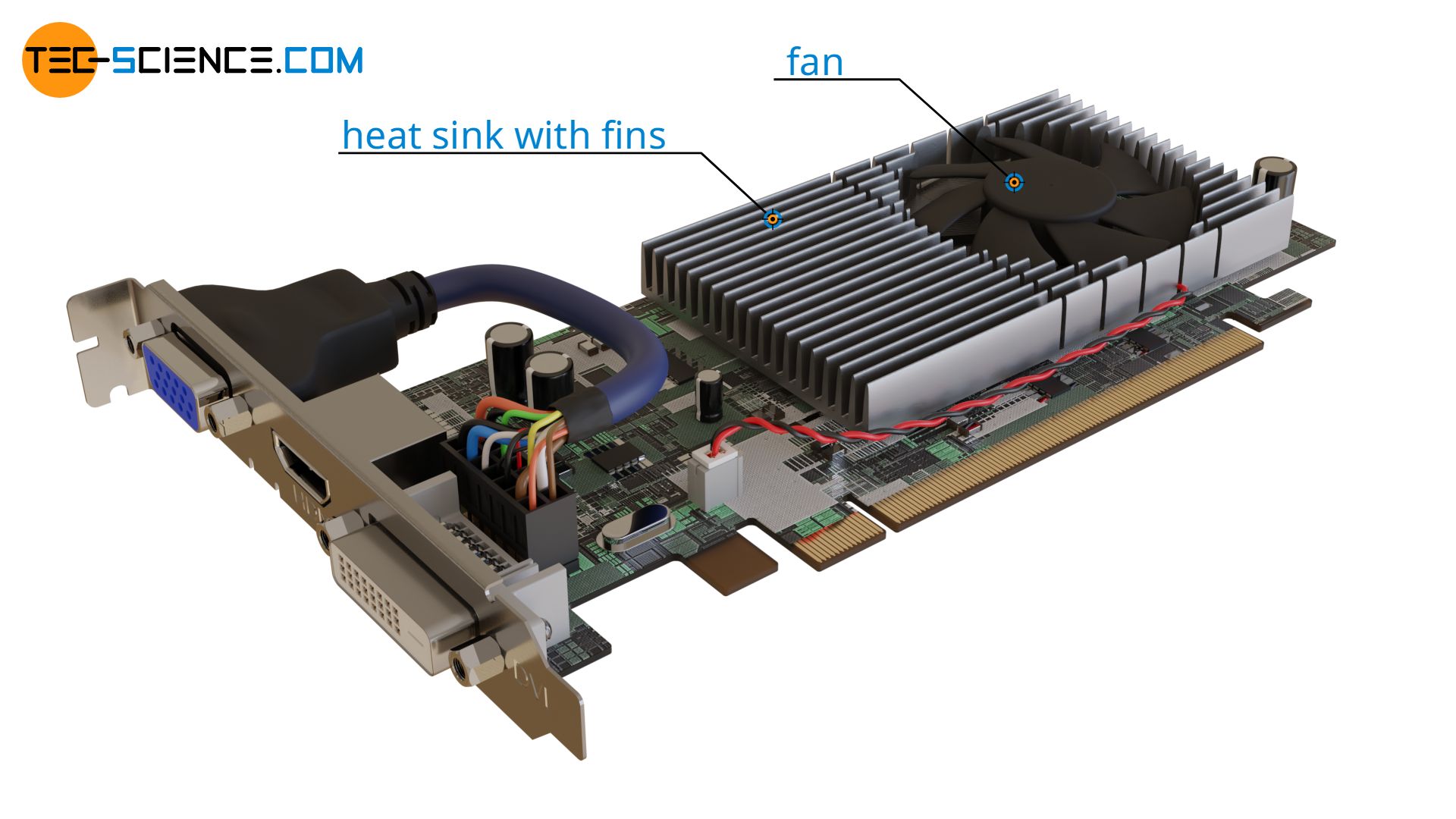

공용 화장실에 위치한 방열기도 이러한 fin analysis의 적용입니다.

https://www.youtube.com/watch?v=BoIHrjZBFfU
General Equation for Fin Analysis
열전달 문제에서 알아내야 하는 것은 온도 분포(Temperature Distribution)와 그로 인한 heat rate(또는 heat flux)입니다.
fin에서 temperature distribution을 구하기 위한 미분방정식을 유도해봅시다.
fin에서의 열전달을 steady-state 라 가정하고 energy balance equation을 세우면 다음과 같습니다.
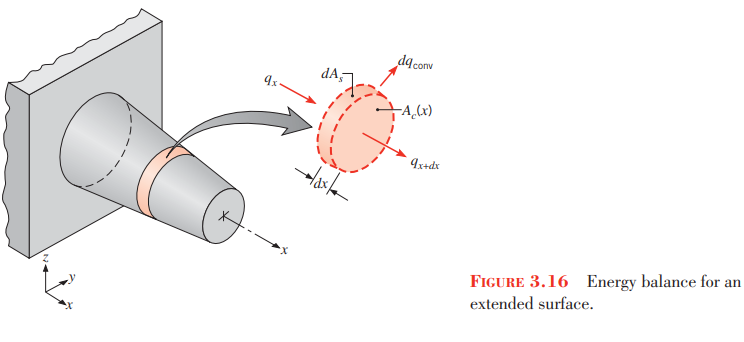
위 그림에서 Ac는 단면적(cross-sectional area), As는 표면적(surface area; 측면 면적) 입니다.
단면 방향으로는(단면에 수직한 방향) 전도(conduction)가 일어나고 측면으로는 대기와 대류(convection)가 일어난다고 생각합시다. (복사 무시)
그럼 들어오는 열과 나가는 열이 같아야 하니 다음과 같은 식을 얻을 수 있습니다.
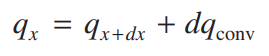
여기서 qx는 x방향 전도이므로 푸리에 법칙(Fourier's law)을 적용해 표현할 수 있습니다.

q_x+dx는 다음과 같이 표현할 수 있습니다.
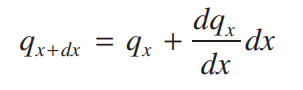
q_x+dx 에 마찬가지로 푸리에 법칙을 적용합니다. 여기서 k가 상수라는 가정이 사용되어 미분기호 밖으로 빠져나왔습니다.

미소 대류 열전달(dq_conv) 항은 다음과 같이 표현됩니다.
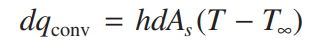
h,T는 property이고 "미소" d를 취했을 때 변하는 것은 As 뿐이므로 우변에 dAs가 된 것입니다.
위와 같이 정리한 세 항을 처음 에너지 관계식에 넣어 정리합니다.
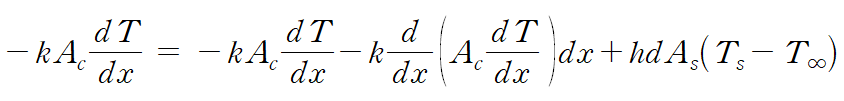
좌변과 우변에 같은 항을 소거하고
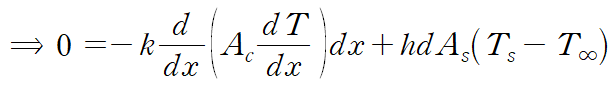
양변을 dx로 나누어 표현하면 다음과 같은 general equation을 얻습니다.
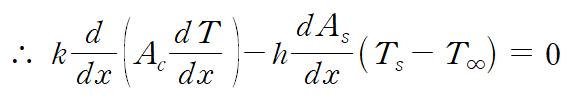
> 사용된 가정 정리
1. neglect radiation
2. 1-dimensional anlysis
3. steady-state
4. constant k
'기계공학 > 열전달' 카테고리의 다른 글
| [열전달] 1D transient conduction(1) : Lumped Capacitance Method (1) | 2024.01.06 |
|---|---|
| [열전달] 1차원 전도 예제(with heat generation) (1) | 2023.11.16 |
| [열전달] 1차원 전도 예제(1D conduction example) (0) | 2023.11.05 |
| [열전달] 열전도 확산방정식 유도 (0) | 2023.11.05 |