(1) Homogeneous Equation

실수 α 에 대해 위 꼴로 정리되는 함수 f(x,y)를 동차함수(homogeneous function)이라 합니다.
아래와 같은 미분방정식에 대해
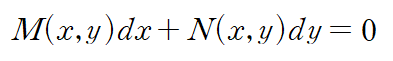
M과 N이 모두 동차함수인 것을 동차미분방정식 이라 합니다.
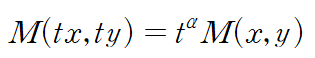

<동차미방의 예시>

dx 앞에 붙은 함수의 동차성 검증
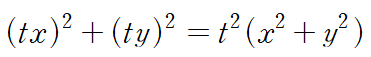
dy 앞에 붙은 함수의 동차성 검증
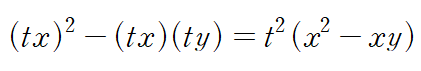
위 방정식의 경우 M(x,y)와 N(x,y) 가 모두 2차 동차함수(homogeneous function of degree 2) 라 부릅니다.
만약 M과 N이 모두 동차함수이며 그 차수가 동일하다면 u = y/x 또는 v = x/y 라 치환하여 보다 쉽게 미분방정식의 해를 구할 수 있습니다(u, v 는 임의의 함수). 치환하게 되면 간단한 변수분리형 미분방정식을 얻습니다.
예시로 든 미분방정식의 해를 구해봅시다.
y = ux 로 잡던, x = vy 로 잡던 상관없습니다. 어느쪽이 계산이 편리할 지는 연습을 통해 감을 얻을 수 있습니다.
이 문제의 경우 y = ux 로 치환하고 치환 식의 양변을 x에 대해 미분합니다.


이것을 처음 미분방정식에 대입합니다.
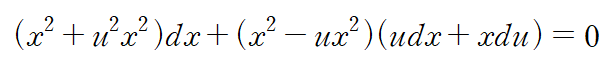

양변을 x^2 로 나누고 dx, dy에 대해 간단히 정리합니다.


변수분리형 미분방정식이므로 아래와 같이 나누고 해를 얻을 수 있습니다.

해를 구하고 마지막에 u = y/x를 이용해 x,y에 대한 식으로 표현해주면 됩니다.
(2) y' = f(ax+by+c)

위와 같은 형태의 미분방정식은 완전미분방정식으로 간주하여 적당한 적분인자를 구하는 것도 어렵고 변수분리도 불가능한 경우가 많습니다.
u = ax + by + c 라 치환해주면 간단하게 풀 수 있습니다.
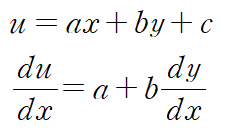

위 식을 처음 미분방정식에 대입합니다.


f(u)가 u에 대한 일차식이라면 선형방정식이라 가정하고 풀면 되고 아니라면 변수분리하여 해를 얻으면 됩니다.

<예제>

u = x + y 로 치환합니다.
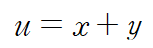
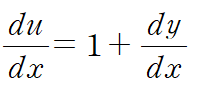

비선형 방정식이니 변수분리해서 해를 구합니다.
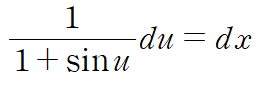
양변을 적분해야 하는데 좌변은 1-sin u를 분모와 분자에 곱해 간단히 정리할 수 있습니다.


양변을 적분하면

위 식에 u = x + y 를 대입해 x와 y에 대한 식으로 바꿔주면 끝입니다.

'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 스토크스 정리(Stokes' Theorem) 예제 (0) | 2022.12.13 |
|---|---|
| [공업수학] *편미분 방정식 예제 : 라플라스 변환* (0) | 2022.06.17 |
| [공업수학] 1계 상미분방정식 총정리 (1) : 변수분리형, 완전미분방정식, 선형 상미분 방정식, 베르누이 방정식 (1) | 2022.03.19 |
| [공업수학] 코시 적분 정리와 공식 (Caychy's Integral Theorem, Formula) (0) | 2021.12.19 |
| [공업수학] 코시-리만 방정식(Cauchy-Riemann Equations) 예제 (2) | 2021.12.07 |