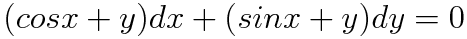SUBORATORY

완전미분방정식이 무엇인지, 어떻게 판별하는지, 어떻게 푸는지에 대해서는 아래 링크를 참조바랍니다. 풀이과정이 다소 길고 복잡하기 때문에 예제 파트를 따로 나누었습니다. 이번 포스팅에서는 네 개의 미분방정식 예제를 소개하는데, 이를 통해 완전미분방정식에 대한 감이 잡히길 바랍니다..! blog.naver.com/subprofessor/222094820066 (예제 1) 다음 미분방정식의 완전성을 검사하여라 dx앞에 있는 놈들을 y에 대해 편미분해주고, dy앞에 있는 놈들을 x에 대해 편미분해줍니다. 음! 뭔가 둘이 안맞네 하죠? 맞아요 완전미분방정식이 아닙니다. 이런 간단한 문제가 시험에 나올 일은 없지만 만약 나온다면 저는 이렇게 답안을 작성할 것 같네요 해당 미분방정식에 대해 완전성 검사를 시행한 결과..

​ 세상에서 가장 아름다운 등식으로도 불리는 Euler's Formula 에 대해서 알아봅시다 ※이 글을 이해하기 위해서는 테일러 급수전개에 대해 알고 있어야 하므로, 모르는 사람들은 아래 링크를 참조합시다※ blog.naver.com/subprofessor/222106300471 ​ 아래 식과 같이 e를 밑으로하는 지수함수와 삼각함수 간의 관계를 나타낸 것을 오일러 공식이라고 한다. 뜬금없이 지수함수와 삼각함수의 관계가 성립한다고? 게다가 복소수까지 콜라보되어 있는 놀라온 공식이다... 양변에 x=π를 대입하고 정리하면 아래 식이 나오는데, 이 식은 세상에서 가장 아름다운 등식으로 불린다 ​ The Most Beautiful Equation ​ ​ ​ ​ 이 세 가지 급수전개 간에 관계가 있다는 것을 ..

오늘은 Erwin Kreyszig 의 Advanced Engineering Mathematics 에 수록된 선적분 예제를 풀어보자 ​ PART 1) 일반적인 선적분 계산 를 구하여라 ​ ​ (예제 1) ​ ​ ​ ​ (예제 2) ​ ​ ​ ​ ​ ​ (예제 3) ​ 곡선 C는 위와 같다 ​ ​ ​ ​ PART 2) C가 폐곡선인 경우 를 구하여라 ​ (예제 1) ​ ​ 경로를 매개변수 t 로 나타내면 아래와 같다 ​ 곡선 C가 폐곡선이므로 선적분은 폐곡선에 대한 선적분이다 ​ 사실 그린정리나 스토크스 정리 등이 아니라 일반적인 선적분 계산 문제에서는 폐곡선이냐 아니냐가 딱히 중요하지 않습니다. 생긴것만 저렇게 생겼지 동일한 방법으로 계산합니다 ​ ​ ​ ​ PART 3) F가 경로 독립(Path Inde..

사실 공업수학에서 미분방정식의 해를 구하기 위해 사용하는 방법이지만 별도로 미분적분학에 먼저 포스팅한다. ​ 라플라스 변환은 미분방정식을 대수방정식 꼴로 변환시켜 보다 쉬운 방정식을 풀 수 있다는 이점을 가지고 있는 변환법이다. ​ 대수방정식은 이런 애들을 칭하는 말이다. 대수적인 특성을 가지고 있는 방정식을 의미하며(당연히..) 사칙연산을 통해 해를 구할 수 있는 방정식을 의미한다. 미분방정식은 미분개념과 적분개념이 모두 포함되어 있는 방정식인데, 이 방정식은 애초에 사람이 인지하기가 어렵다. 변화율을 인지하는 것 자체가 어렵기도 하고 지수함수나 삼각함수와 같은 초월함수들이 포함될 경우 더더욱 이해하기가 어렵다. 반면 대수방정식은 인수분해 또는 근의 공식을 통해 쉽게 해를 구할 수 있다는 장점이 있다...

푸리에 급수란? 푸리에 급수(Fourier Series) 는 삼각함수들의 합으로 주기함수를 나타내는 방법이다. 나중에 푸리에 적분에서는 주기함수라는 조건이 무의미해지는 지경까지 이른다.(주기를 무한대로 잡은 것..) "대체 이걸 어떻게 떠올린 거지?"라는 생각이 안 날 수가 없는 위대한 발견이다. 푸리에 급수는 파동분석을 하기 위한 기초 개념이다. 푸리에 변환은 주기함수건, 비주기함수건 상관없이 삼각함수의 합 꼴로 함수를 해석할 수 있게 도와주는 도구다. 파일 압축에도 사용된다는데 거기까지는 아직 내 분야가 아니라 Pass.. 우리의 목표는 푸리에 변환까지다. 아무튼 이 "푸리에 XX"를 통틀어 푸리에 분석(Fourier Analysis)이라고 부른다. 아무튼 그 푸리에 분석의 기초가 되는 '푸리에 급수..

미분방정식이란 말은 왠지 모르게 멋있다. 고등학교 들어와서 '미분방정식'푸는 공대 형들이 참 멋있어보였다. 나만 그런가..? 아무튼, 실제로 미분방정식은 "멋있다." 자동차를 굴리는 힘인 엔진에서도 미분방정식을 빼놓고 설명할 수 없으며 바짓주머니 속에 있는 스마트폰에서도, 릴라드가 던진 클러치 3점슛에서도 미분방정식은 등장한다. 공업수학을 배우고 나면 사회 전반에 미분방정식이 관여하고 있음을 깨닫는다. 도대체 미분방정식이란 게 뭘까? (i) 미분방정식? 미분방정식이라는 건 [미분]+[방정식] 같은 느낌으로 이해하면 된다. 고등학교 때 배우는 미적분과 초등학교 때 배우기 시작하는 방정식의 '역대급' 콜라보랄까? 한창 과외를 할 때 방정식의 정의를 모르는 학생들을 참 많이 만났다. 방정식의 정의는 다음과 같..

공업수학 포스팅은 Erwin Kreyszig 의 Advanced Engineering Mathematics 10th edition 즉 공업수학 10판을 기반으로 하며 상미분 방정식만을 다룬다. 교재의 로드맵을 이용해 보여주면 다음과 같다. 기회가 되면 PART B도 포스팅할 것 같은데 일단 계획은 상미분 방정식까지만. 편미분 방정식부터는 너무 괴랄하고 복잡한 데다가 필요한 사람의 풀(pool)이 너무 좁아지기 때문에 굳이 포스팅하지 않는다. (사실 내가 잘 몰라서_.._) 포스팅 목적 자체가 일반인들도 마치 잡지 읽듯이 부담감 없이 읽을 수 있도록 '소개'하는 것 그리고 쉬운 설명이 필요한 전공인들에게 '이해'를 돕는 것에 있기 때문에 PART A까지만 포스팅한다. 상미분 방정식을 푸는 방법에는 크게 세..