#공업수학
Systems of Linear Differential Equations
연립 선형 미분 방정식 예제입니다.
연립 제차 방정식에 관한 이해가 선행됩니다.
https://subprofessor.tistory.com/129
[공업수학] 연립미분방정식 예제 : 제차 방정식 (Homogeneous Equation)
#공업수학 Systems of Linear Differential Equations 연립 선형 미분 방정식 예제입니다. 라플라스 변환을 사용하지 않으며 행렬과 고윳값으로 해결합니다. 1. Homogeneous Linear Systems 다음과 같은 형태의
subprofessor.tistory.com
또한 비제차 방정식을 푸는 데 필요한 매개변수법과
https://blog.naver.com/subprofessor/222131481613
[공업수학] 2.10-2 매개변수법 증명(유도)과 예제
#공업수학 매개변수법을 이용한 특수해는 아래와 같습니다 어째서 Wronskian이 특수해를 구하는 데에 사용...
blog.naver.com
1. Non - Homogeneous Linear Systems
연립 선형 비제차 방정식의 형태는 제차의 경우와 유사하게 행렬로 표현합니다.
별도의 표기는 되어있지 않지만 X는 마찬가지로 t - domain입니다.
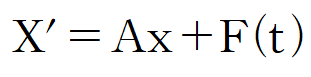
예시는 다음과 같습니다.

연립이 아닌 경우와 마찬가지로 미정계수법과 매개변수법을 사용해 해를 구합니다.
2. Solution
1. 미정계수법(Undetermined Coefficients)
F(t)의 형태를 보고 적절한 특수해를 설정하는 방법입니다. 이때 함수가 계수가 되며 함수 앞에 붙는 계수가 행벡터가 됩니다.
(i) 제차해를 구한다. (homogeneous solution or complementary solution(function))
(ii) 특수해를 구한다. (particular solution)
(iii) 일반해 수립

(i) 먼저 제차해를 구합니다.

제차해는 고윳값 -> 고유벡터 -> 일반해 수립 순으로 구합니다.
다음과 같이 제차해를 구할 수 있습니다.

(ii) F(t)의 형태를 보고 특수해를 설정합니다.

F(t)가 다항함수 형태이므로 다음과 같이 특수해를 다항함수로 설정합니다.
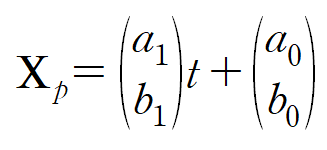
이를 원래 미분방정식에 대입해서 계수를 결정합니다.


1행, 2행 나누어서 등식을 정리하면 아래와 같이 정리되지만

보통 함수 기준으로 세우고 그 다음 행을 비교합니다.
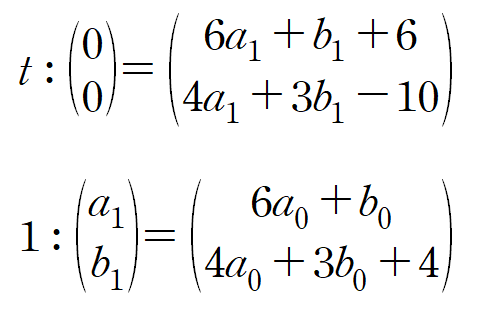
행렬로 정리해서 계수를 구합니다.(그냥 연립해도 상관없습니다)
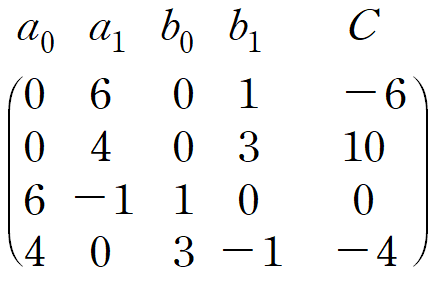
다음과 같이 특수해의 계수가 결정됩니다.
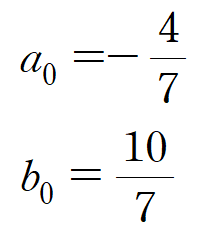
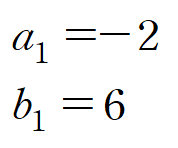

(iii) 제차해와 특수해를 합쳐 일반해를 나타냅니다.

2. 매개변수법(Variation of Parameters)
(i) 제차해를 구하고 Fundamental matrix 수립
(ii) Fundamental matrix의 역행렬 구하기
(iii) F(t)와 곱한 후 적분 하기
(iv) 일반해 수립
매개변수법의 경우 매개로 삼을 solution set을 다음과 같이 정의합니다.

이때 Xn은 제차해의 기저(basis)해입니다. (선형결합 X = c1x1 + c2x2 에서 x1와 x2)
행렬Φ(t)를 fundamental matrix of the system 이라 부릅니다. (저 기호는 파이[phi]라고 읽습니다)
유도과정은 생략하고 해의 형태가 다음과 같이 된다는 것만 가져갑시다.

C는 상수들의 행벡터입니다.
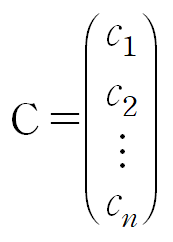
매개변수법을 이용해 아래 미분방정식을 풀어봅시다.

(i) 제차해 구하고 Φ(t) 수립
제차해를 구하는 과정은 생략하겠습니다.
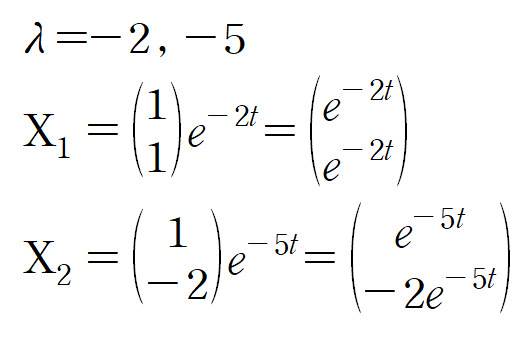

(ii) Fundamental matrix의 역행렬 구하기
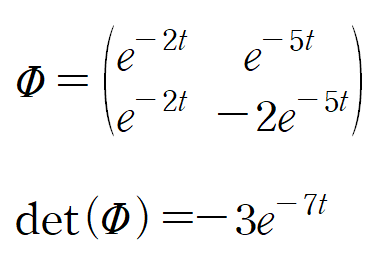

※ 참고 : 2 x 2 행렬의 역행렬 구하는 방법
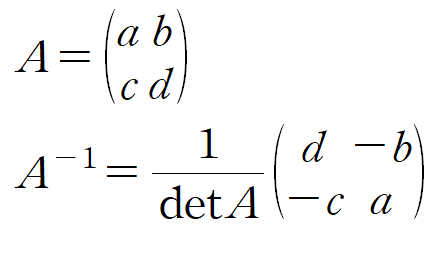
Φ(t)의 역행렬은 다음과 같습니다.
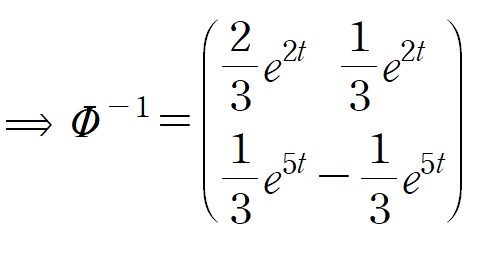
(iii) F(t)와 곱한 후 적분 하기
매개변수법에서는 특수해가 두 번째 적분이 포함된 항이 됩니다.
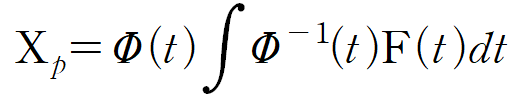

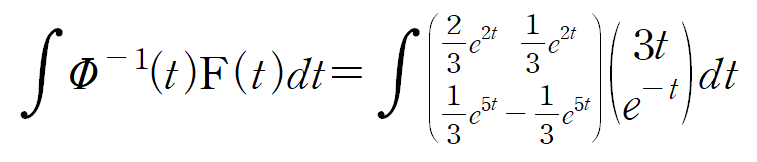

이것을 Φ(t)와 곱합니다

(iv) 일반해 수립
따라서 일반해는 다음과 같습니다.
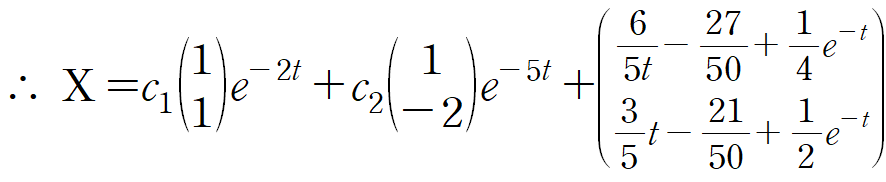
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] Homogeneous Linear ODEs of Second Order에서 중첩원리 증명 (0) | 2023.01.04 |
|---|---|
| [공업수학] 1.5-2 베르누이 방정식(Bernoulli Equation) (3) | 2023.01.02 |
| [공업수학] 1.5-1 선형 상미분방정식(Linear ODEs) (1) | 2022.12.30 |
| [공업수학] 1.4-3 적분인자(Integrating Factor) (2) | 2022.12.30 |
| [공업수학] 1.4-2 완전미분방정식 예제 (0) | 2022.12.29 |