반응형
#선형대수학
2차원 평면에서 반시계방향으로 θ만큼 회전한 회전행렬은 다음과 같이 표현된다
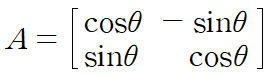
열벡터 형태로 표시된 [x,y]를 이 행렬에 곱하면 반시계방향으로 θ만큼 회전이 된다.
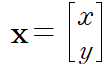
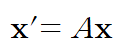
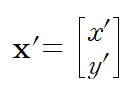
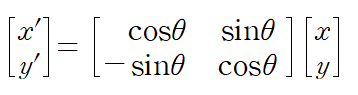
여기서 [x,y]가 의미하는 것은 점이 될 수도 있고, 도형이 될 수도 있다.
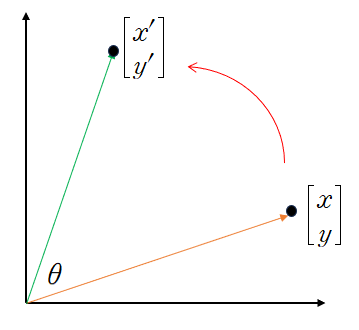
이것을 사용해 이차곡선을 회전시킬 수도 있다.
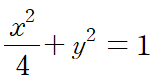
위 타원을 반시계방향으로 45도 회전한 도형의 방정식을 구해보자
먼저 회전행렬을 정의하고
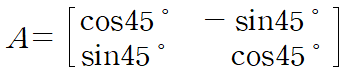
그 다음 회전 변환 식을 이용해
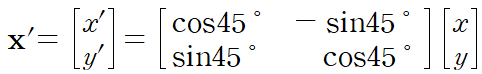
x', y' 에 대한 식을 얻는다.
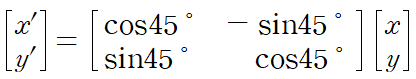
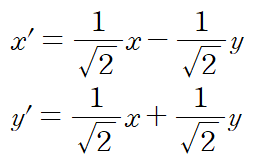
우리가 가지고 있는 것은 x, y에 대한 관계식(타원의 방정식)이므로
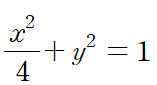
x와 y에 대해 식을 정리해서 넣어주자
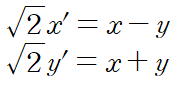
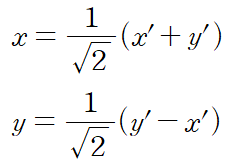
타원에 방정식에 정리한 x, y를 넣어주고 정리하면
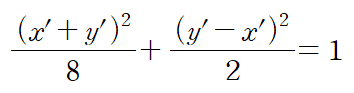
아래와 같은 식을 얻는다.
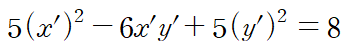
프라임(')을 날려주면 회전된 도형의 방정식을 얻는다.
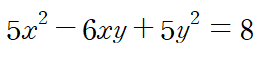
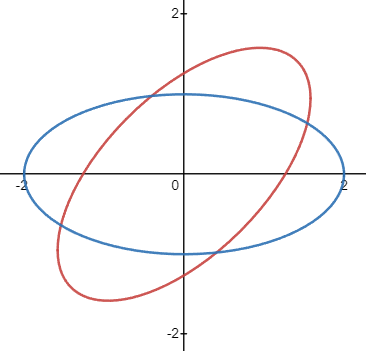
회전 변환이 타원, 쌍곡선, 포물선과 같은 이차곡선에만 한정되는 것은 아니다.
이차함수에도 적용 가능하고
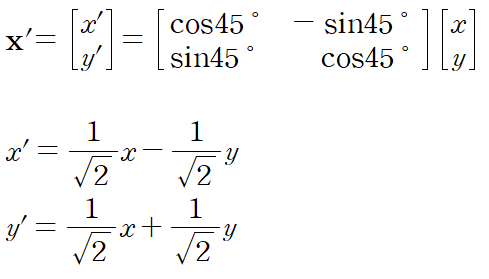
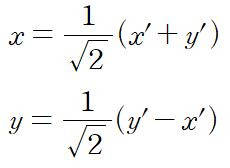
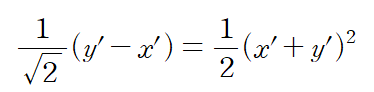
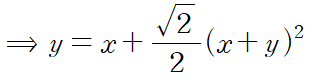
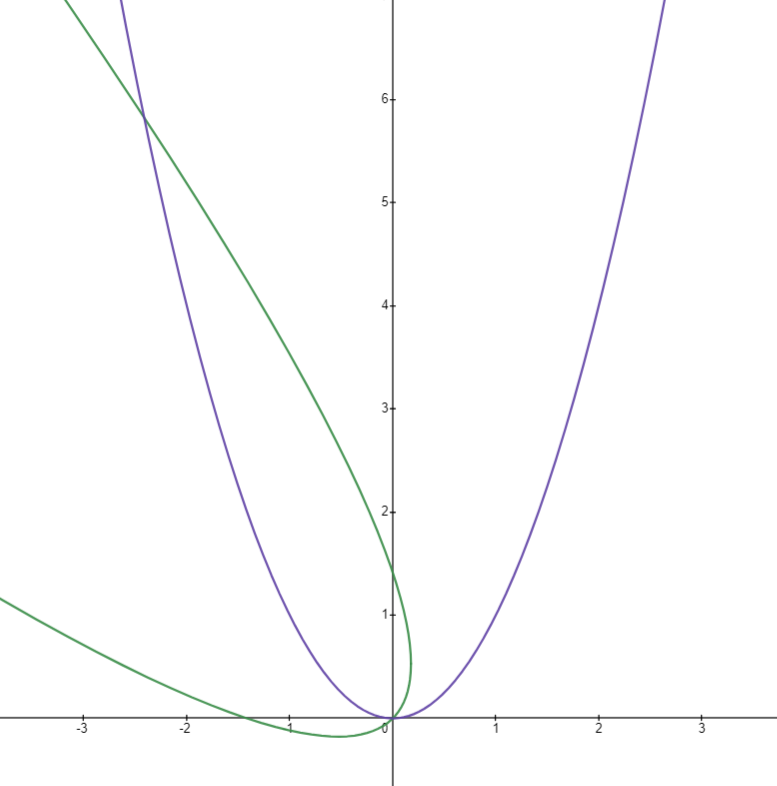
초월함수에도 적용할 수 있다.
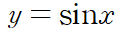
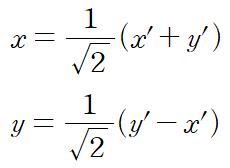
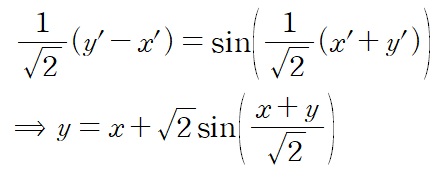
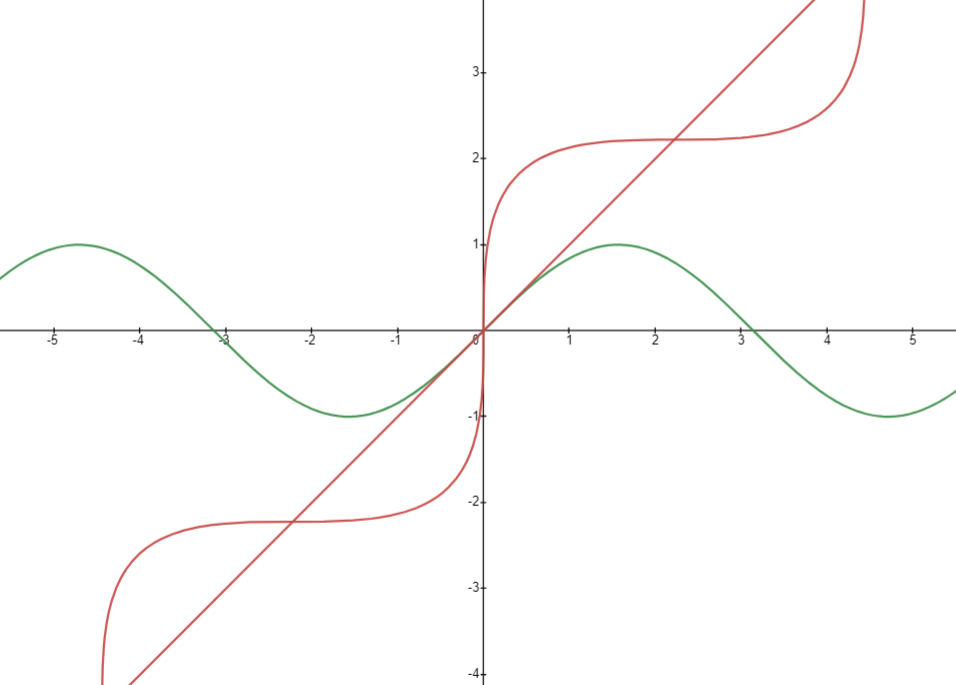
단지 explicit function (y = f(x)) 형태로 표현이 안 될 뿐이지 모두 회전할 수 있다.
반응형
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| 특이값 분해(Singular Value Decomposition; SVD) 예제 (0) | 2024.05.23 |
|---|---|
| [선형대수학] 선형방정식, 연립방정식 예제 (0) | 2024.04.23 |
| [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지 (1) | 2023.12.12 |
| [선형대수학] 최소제곱법 (Method of Least Squares) (0) | 2022.08.17 |
| [선형대수학] 케일리-해밀턴 정리 : 행렬의 거듭제곱, 역행렬 (Cayley–Hamilton theorem) (0) | 2022.08.15 |