반응형
#선형대수학
단위행렬 I 에 대해서는 행렬을 인수분해처럼 다뤄도 괜찮다.
어차피 행렬곱 과정에서 소거가 되기 때문인데요, 예제를 보겠습니다.
(예제 1) 행렬 M에 대하여 M^3를 구하여라. 이때 행렬 M의 세제곱을 직접적으로 계산해서는 안된다.
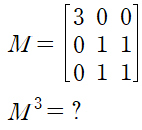
아래와 같이 행렬 M을 인수분해할 수 있습니다.
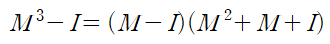
이렇게 인수분해할 수 있는 것은 단위행렬이기 때문입니다.
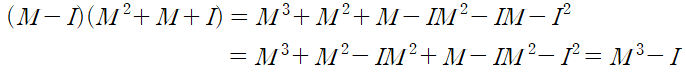
분해된 행렬을 계산하는 것은 비교적 간단합니다.
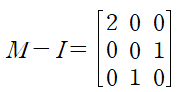

따라서 M의 세제곱은 아래와 같이 계산됩니다.
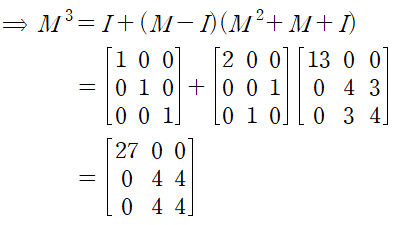
이보다 더 깔끔한 상황이 있습니다.
(예제 2) 주어진 행렬을 적절한 두 행렬의 합으로 표현하여 역행렬을 구하여라
Hint : 행렬의 거듭제곱
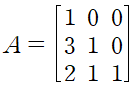
반응형
먼저 A를 I+B로 분해할 수 있습니다.
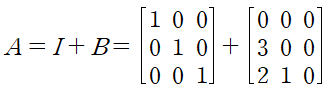
이때, I+B^3은 다음과 같이 분해됩니다.
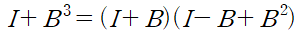
대각성분이 없는 삼각행렬의 경우 한 번 거듭제곱할 때마다 요소가 한 줄씩(대각선 방향) 없어집니다.
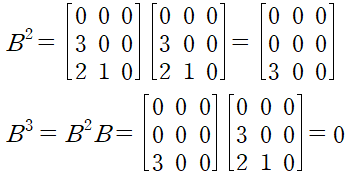
따라서 위에서 세운 인수분해식은 A를 포함한 상당히 간단한 식이 됩니다.
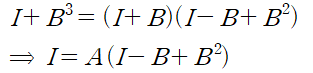
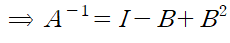
앞서 계산한 B와 B의 제곱을 사용해 A의 역행렬을 구할 수 있습니다.
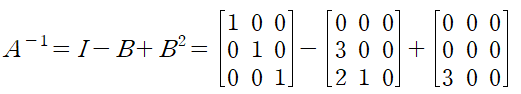
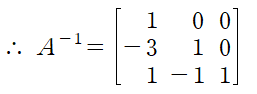
반응형
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| 특이값 분해(Singular Value Decomposition; SVD) 예제 (0) | 2024.05.23 |
|---|---|
| [선형대수학] 선형방정식, 연립방정식 예제 (0) | 2024.04.23 |
| [선형대수학] 회전행렬(Rotation matrix), 회전변환 (0) | 2023.12.28 |
| [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지 (1) | 2023.12.12 |
| [선형대수학] 최소제곱법 (Method of Least Squares) (0) | 2022.08.17 |