#라플라스변환
#공업수학
라플라스변환으로 미분방정식 문제 세 개를 풀어봅시다.
예제 1 : 기본적인 상수계수 2계 미분방정식
예제 2 : 단위계단함수
예제 3 : 디랙 델타
(예제 1) 미분방정식의 해를 구하여라
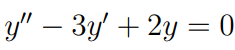
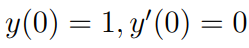
> 도함수 공식
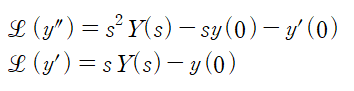
(1) 주어진 미분방정식의 양변에 라플라스 변환을 취합니다.
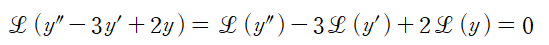
도함수 공식을 적용하고
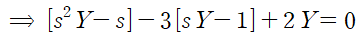
Y에 대해 정리합니다.
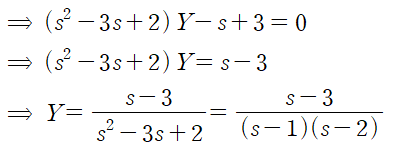
(2) 부분분수 분해
부분분수 분해란 분자의 차수가 분모보다 낮은, 가장 간단한 분수 형태로 쪼개어 표현하는 것을 말합니다.
어렵지 않습니다.
미지의 상수 a,b 를 이용해 표현하고 통분하면 끝입니다.
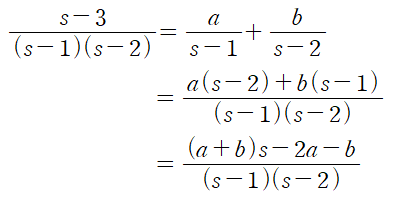
그런 후에 좌변과 우변의 계수를 비교해 a, b를 결정합니다.
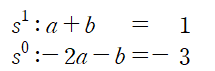
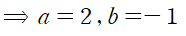
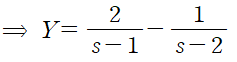
(3) 라플라스 역변환을 거쳐 y(t)를 구합니다.
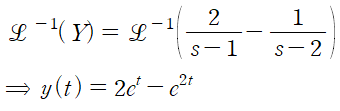
(예제 2) 미분방정식의 해를 구하여라
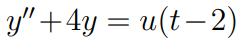
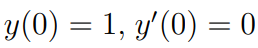
단위 계단 함수(unit step function, heaviside function)에 대한 자세한 내용은 아래 글 참조 바랍니다.
[공업수학] 6.3 단위계단함수, t-shifting
#공업수학 #라플라스변환 구간에 따라 나뉜 함수. 예를 들면 x>0에서 x^2 이고 x<0에서 3x인 함수가 ...
blog.naver.com
아래 공식만 기억하면 단위 계단 함수 문제를 풀 수 있습니다.
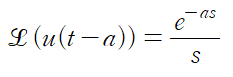
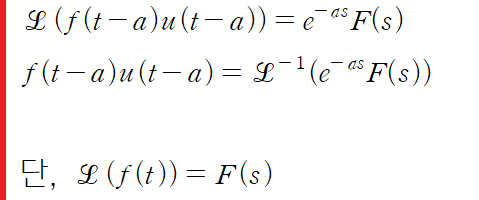
(1) 양변에 라플라스 변환을 취합니다
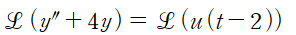
마찬가지로 Y에 대해 정리하는 것이 목표입니다.
단위 계단 함수의 라플라스 변환은 아래와 같습니다.
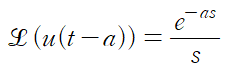
a=2인 경우이므로 다음과 같이 정리됩니다.
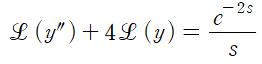
앞선 예제와 동일하게 도함수 공식을 적용하고 정리합니다.
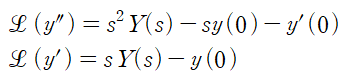
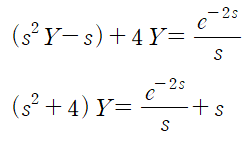
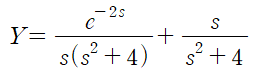
(2) t-이동정리를 사용해 역변환
변환표로부터 적절한 역변환을 수행합니다.
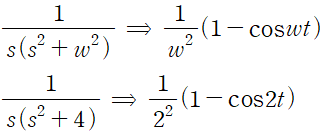
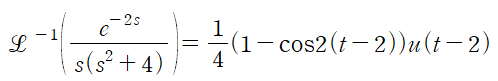
> t-이동정리
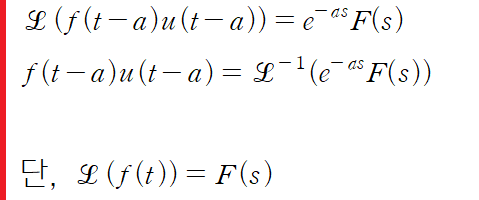
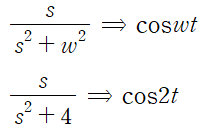
따라서 정리하면 미분방정식의 해는 다음과 같습니다.
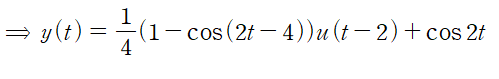
(예제 3) 미분방정식의 해를 구하여라
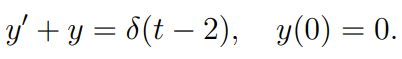
디랙 델타의 라플라스 변환만 가지고 넘어갑시다.
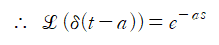
(1) 양변에 라플라스 변환을 취합니다.
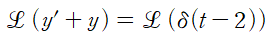
디랙 델타의 변환을 적용하고
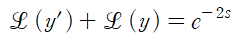
도함수 공식을 적용합니다.
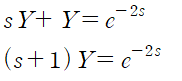
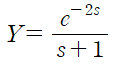
(2) t-이동정리를 사용해 역변환
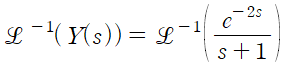
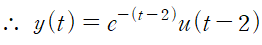
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| 푸리에 급수 예제 (0) | 2024.02.27 |
|---|---|
| [공업수학] dominant eigenvalue와 고유값의 근사, MATLAB code (0) | 2024.01.05 |
| [공업수학] 미분방정식의 멱급수 해법(Power Series Method) (0) | 2023.07.19 |
| 라플라스 변환 공식 모음 (0) | 2023.04.15 |
| [공업수학] 2.7-1 2계 비제차 미분방정식 : 미정계수법(Method of Undetermined Coefficients) (1) | 2023.01.21 |