#공업수학
[공업수학] 2.2-1 상수계수를 가지는 제차 선형 상미분 방정식 (Homogeneous Linear ODEs with Constant Coeffici
공업수학(상)(Kreyszig)(Kreyszig)(10판) 『Kreyszig 공업수학, 10판』 상권. 이 책은 반세기 동안 전 세계적으로 가장 널리, 그리고 가장 많이 채택되어 사용되고 있는 Erwin Kreyszig 교수가 저술한 Advanced Engi
subprofessor.tistory.com
이제 챕터 2도 거의 마무리되어 가네요. 오늘은 2계 미분방정식 로드맵 끝에서 두 번째에 위치한 미정계수법에 대해서 알아봅시다. Nonhomogeneous 즉 비제차 방정식의 해를 구하는 미정계수법은 기본적으로 제차방정식의 해를 구할 수 있어야 합니다. 제차 방정식의 일반해를 구하고 거기에 특수해를 더하는 형식이기 때문에 개념이 확실하지 않은 분, 2계 미분방정식의 제차 방정식의 일반해를 구할 수 없는 분은 위 관련 포스팅 링크를 통해 복습해주시기 바랍니다.

2계 미분방정식 로드맵
비제차 방정식의 정의
비제차 방정식의 해를 구하는 매개변수법에 대해 알아보기 전에 비제차 방정식의 정의에 대해서 다시 한 번 짚고 넘어갑시다
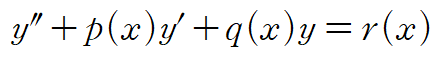
2계 선형 미분방정식의 일반형
x로만 이루어진 항 r(x)가 0이면 제차 방정식, 0이 아니면 비제차 방정식입니다
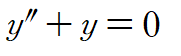
위 방정식은 제차 방정식이고, 일반해가 y=Acos x + Bsin x 였습니다.(이전 포스팅 참조)
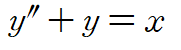
위 방정식은 r(x)가 1 즉 0이 아니므로 비제차 방정식입니다. 그런데 이 방정식의 해는 어떻게 구할 수 있을까요? 지금까지 우리는 방정식의 형태를 보고 해를 가정했습니다. 상수계수로만 이루어진 방정식은 자연상수를 밑으로 갖는 지수함수 형태로, 오일러-코시 방정식은 다항함수의 형태로 해를 가정하고 일반해를 구했죠. 근데 두 방법 중 어떤 방법을 사용하더라도 위 방정식의 해를 구하는 건 어려워보입니다. 지수함수로 가정하더라도, 다항함수로 가정하더라도 쉽게 풀리지가 않아요. 그래서 새로운 방법 미정계수법이 등장합니다
(i) Basic Concept
비제차 방정식의 해를 구하는 Basic Concept는 다음과 같습니다
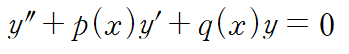
위 제차 방정식의 해를
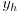
라 하고(homogeneous 를 따서 h를 아래 첨자로 붙임)

위 비제차 방정식의 해를

라 할 때 다음이 성립합니다

우변의 두번째 항은 particular solution(특수해) 을 따서 p를 아래 첨자로 붙여 표현합니다. 이때

는 미지의 상수
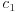
,

을 포함하는 일반해이고,

는 미지상수가 없는 특수해입니다. 저 특수해

를 구하는 두 방법이 바로 오늘 배울 미정계수법과 Wronskian을 이용한 매개변수법입니다. 미정계수법은 먼저 r(x)=0인 제차방정식의 해를 구하고, 그 다음 구한 일반해로부터 특수해를 가정해 푸는 방법입니다.
(ii) 미정계수법(Method of Undetermined Coefficients)
이름이 미정계수법인 이유는 간단합니다. 특수해를 미정계수가 포함된 꼴로 가정하고 그 다음 미정계수를 확정짓는 방식으로 비제차 방정식의 해를 구하기 때문입니다. 미정계수법에는 세 가지 Rule이 적용되는데 그 Rule을 따라 특수해를 설정하고 비제차 방정식의 해를 구하면 됩니다

첫 번째, Basic Rule 입니다. 왼쪽 r(x)에 대응되는 함수를 찾아서 특수해를 설정합니다

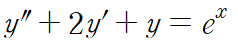
예를 들어 위 비제차 방정식의 경우
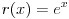
이므로
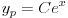
라고 특수해를 설정하면 됩니다. 오른쪽 특수해 표를 보면 모르는 상수들이 보이죠? 이 미지상수들은 특수해를 주어진 미분방정식에 다시 대입함으로써 확정지을 수 있습니다. 방금 예로 든 비제차 방정식을 다시 봅시다

이 특수해를
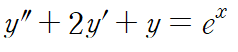
여기에 대입할 겁니다
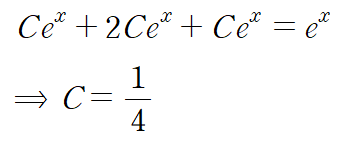
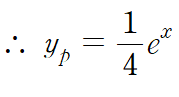
이런 식으로 특수해를 구하시면 됩니다
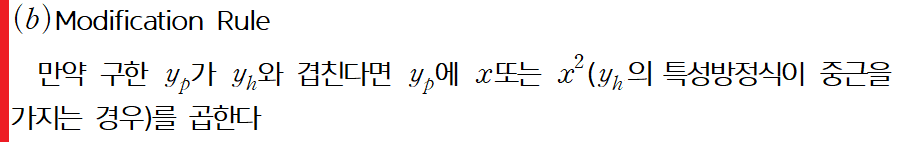
ex1)
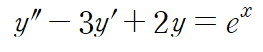
위 제차방정식의 경우 Basic Rule을 적용하면

라는 특수해를 설정할 수 있는데요, 제차방정식이 이미
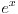
를 포함하기 때문에 Modification Rule을 적용해주어야 합니다
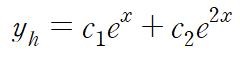
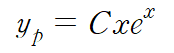
ex2)

이번에는 제차방정식의 특성방정식이 중근을 가질 경우를 봅시다

제차방정식의 해가 이미
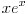
를 가지고 있기 때문에 특수해는 다음과 같이 설정할 수 있습니다



이런 식으로 합의 꼴 r(x)가 주어지면 특수해도 합의 꼴로 설정하면 됩니다
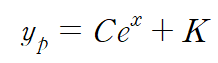
이렇게 말이죠
항상 그런 것 같습니다. 생소할 뿐이지 어려운 내용은 아닙니다. 만약 어렵게 느껴진다면 단지 익숙치 않아서 그렇게 느껴질 뿐이라는 걸 기억하시고 포기하지 않으셨으면 합니다. 이번 포스팅에서 다룬 미정계수법 개념은 여기서 마무리하고 다음 포스팅에서 미정계수법 예제를 다뤄봅시다.
Any Qustions, Any Comments WELCOME :)
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 미분방정식의 멱급수 해법(Power Series Method) (0) | 2023.07.19 |
|---|---|
| 라플라스 변환 공식 모음 (0) | 2023.04.15 |
| [공업수학] 2.6 론스키 행렬식(Wronskian) (0) | 2023.01.11 |
| [공업수학] 2.5 오일러-코시 방정식 (Euler-Cauchy Equation) (0) | 2023.01.10 |
| [공업수학] 편미분 방정식 (3) : 비제차 방정식(Time-dependent) (0) | 2023.01.07 |