#선형대수학
> 미리보기
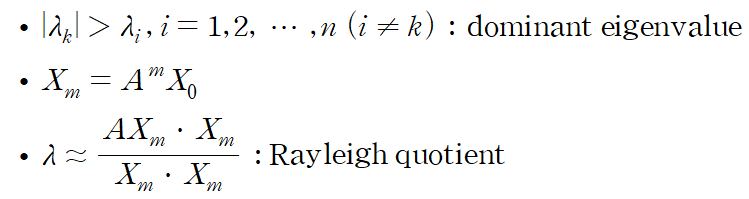
1. Approximation of Eigenvalues
행렬의 거듭제곱(power method)을 계산하여 고유값의 근사치를 구할 수 있습니다.
Xm이 행렬의 거듭제곱과 어떤 벡터 X0의 곱으로 정의될 때
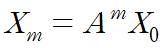
고유값은 다음과 같이 근사할 수 있습니다.
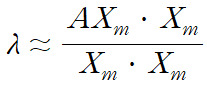
위 식의 우변을 Rayleigh quotient라 부릅니다.
예시로 아래와 같은 2x2 행렬을 봅시다.
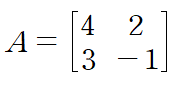
먼저, 임의의 X0를 설정합니다.
통상적인 고유값 계산 과정은 행렬식을 이용하는 것이지만 우리는 다른 방법으로 고유값의 근사치를 구할 것입니다.
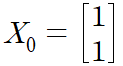
연산이 많으니 가급적 간단한 X0를 사용하는 것이 좋겠죠?
다음으로 행렬의 거듭제곱을 사용해 적당히 큰 Xm을 얻습니다.
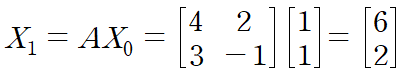

이를 반복해 X7까지 구해주었습니다.
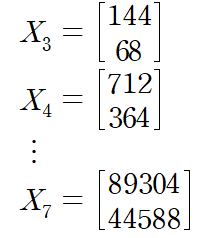
이제 고유값을 근사해봅시다
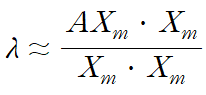
본격적인 연산 전에, X7이 너무 크니 스케일링 해주겠습니다.
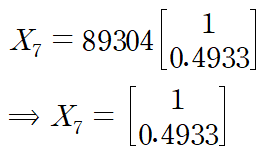
이것을 근사식에 대입합시다
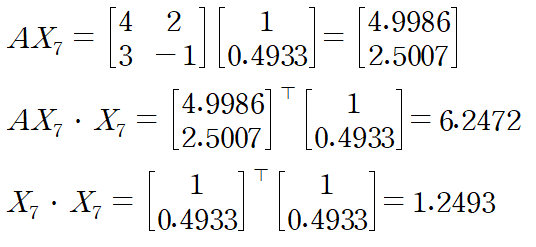
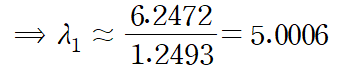
근사식을 사용해 얻은 고유값은 5.0006입니다
고유값의 정의를 사용해 얻은 실제 고유값은 5, -2이니 근사가 잘 되었네요
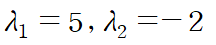
2. Dominant Eigenvalue
사실 위에서 알아본 근사식은 그냥 고윳값이 아니라 "Dominant Eigenvalue"을 구하는 근사식입니다.
Dominant Eigenvalue의 정의는 다음과 같습니다.
n x n 행렬 A와 i = 1,2, . . . , n에 대하여 다음과 같은 k번째 고유값을 A의 dominant eigenvector라 한다.
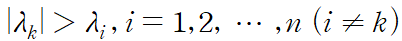
즉 절댓값이 가장 큰 하나의 고유값을 의미합니다.
예를 들어
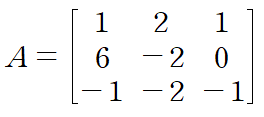
위 행렬의 고유값을 구해보면 0, -4, 3 이니
dominant eigenvalue는 -4가 됩니다.
아래의 행렬 B의 경우 고유값이 2, 5, 5 입니다.
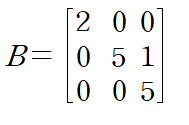
이때 dominant eigenvalue는 5가 아니라 "존재하지 않는다"가 됩니다.
이점을 주의해야 합니다.
=> dominant eigenvaule : 절댓값이 가장 큰 고유값
=> 만약 절댓값이 가장 큰 고유값이 2개 이상이면 dominant eigenvalue는 없다(λ = -5, 5 처럼)
3. MATLAB Example
(예제) 3 x 3 행렬 A에 대해 dominant eigenvalue를 구하여라
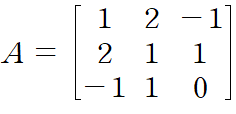
임의로 10번 연산을 수행해 dominant eigenvalue를 근사하였습니다.
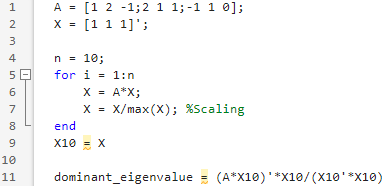
A = [1 2 -1;2 1 1;-1 1 0];
X = [1 1 1]';
n = 10;
for i = 1:n
X = A*X;
X = X/max(X); %Scaling
end
X10 = X
dominant_eigenvalue = (A*X10)'*X10/(X10'*X10)

실제 A의 고유값은 다음과 같습니다.
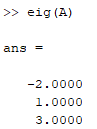
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| 라플라스 변환 미분방정식 예제 (0) | 2024.12.02 |
|---|---|
| 푸리에 급수 예제 (0) | 2024.02.27 |
| [공업수학] 미분방정식의 멱급수 해법(Power Series Method) (0) | 2023.07.19 |
| 라플라스 변환 공식 모음 (0) | 2023.04.15 |
| [공업수학] 2.7-1 2계 비제차 미분방정식 : 미정계수법(Method of Undetermined Coefficients) (1) | 2023.01.21 |