#공업수학
0. Introduction
멱급수란 다항함수들의 합으로 구성된 급수를 뜻하며 앞서 테일러 급수를 통해 함수를 멱급수 형태로 나타내는 방법을 소개했었다.
[미분적분학] 테일러 급수전개
#미분적분학 테일러 급수전개는 미분방정식을 공부하면서도 나오는 내용이고, 어떤 값을 근사하는 데도 사...
blog.naver.com
아래와 같은 형태의 급수를 멱급수라 한다.
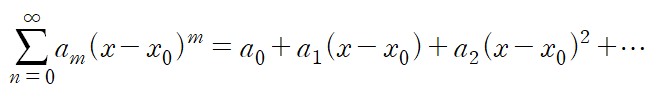
가장 일반적인 형태이며 우리는 x0 = 0 즉, x = 0에서 전개한 멱급수를 사용할 것이다.
지수함수를 아래와 같이 표현할 수도 있고
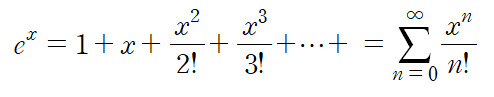
유리함수를 표현할 수도 있다.
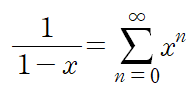
물론 수렴범위가 무한한 것은 아니다. 위 유리함수의 경우 열린구간 (-1, 1) 에서만 급수가 수렴한다.
이것을 응용하여 여러가지 함수를 급수 형태로 나타낼 수 있다.
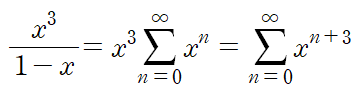
멱급수로 표현된 함수를 미분할 수도 있다.(멱급수 미분)
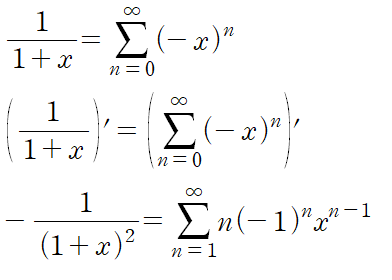
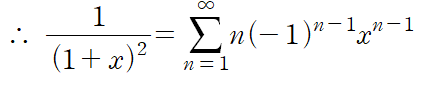
미분방정식의 해를 이러한 멱급수로 가정한 다음 해를 구하는 것을 멱급수 해법(Power Series Method)이라 한다.
1. Power Series Method
아래와 같은 미분방정식을 보자
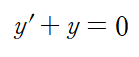
이 미분방정식의 해 y를 아래와 같이 가정한다면 y'는 각 항을 미분한 것의 합과 같다.
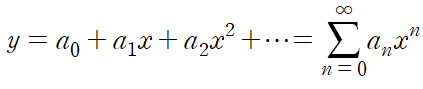
우리의 목표는 멱급수의 계수에 해당하는 수열 {an}을 구하는 것이다.
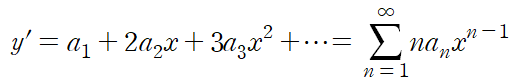
이것을 미분방정식에 대입하여 항별로 정리하면 다음과 같다.
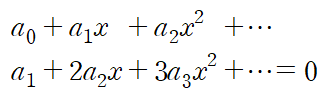
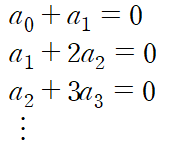
미분방정식의 해는 적분상수가 포함된 함수로 얻어지는데, 1계의 경우 하나의 상수가, 2계의 경우 두 개의 상수가 나온다는 거승ㄹ 우리는 이미 알고 있다. 급수해에서도 마찬가지로 n계 미분방정식을 표현하기 위해 n개의 상수가 요구된다.
통상적으로 이 상수를 a0 또는 a1 처럼 초기에 등장하는 항을 사용한다.
쉽게 말해 위 문제는 1계 미분방정식이므로 a0를 미지의 상수로 갖는 함수를 일반해로 얻게 될 것이고
우리는 수열의 다른 항들을 a0로 표현하면 된다.
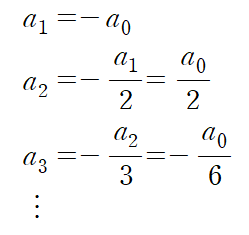
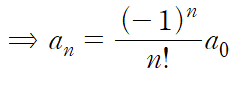
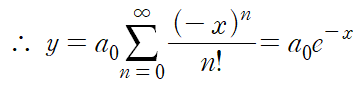
마지막 급수 표현은 가능한데 왜 지수함수로 정리되는지 한 번에 보이지 않을 수 있다.
인수분해를 잘 하기 위해서 곱셈공식을 먼저 연습하듯, 함수들을 급수로 전개하는 연습을 해보면 점점 보이기 시작할 것이다.
대표적인 급수전개는 아래와 같다.
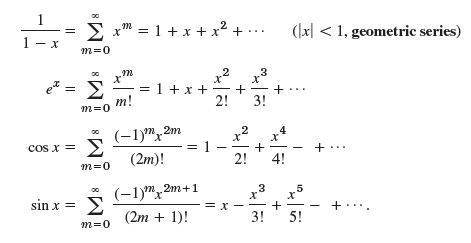
2. Examples
(예제 1) 급수해 방법으로 미분방정식을 풀어라
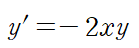
우리는 앞서 한쪽으로 항을 몰아서 계수를 비교하는 방법을 사용했으므로 먼저 우변에 있는 2xy를 좌변으로 이항해 정리한다.
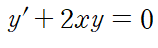
그리고 아래와 같이 해를 가정하고 미분방정식에 대입한다.
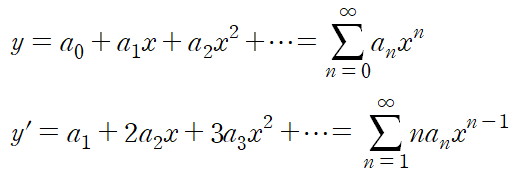
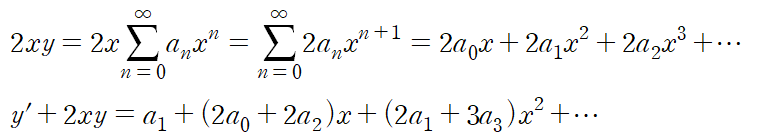
그 다음으로는 계수비교를 통해 수열 {an}을 표현한다.
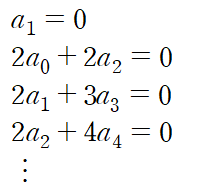
먼저 알 수 있는 것은 홀수 번째 항이 모두 0이라는 것이다.
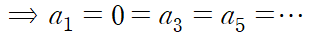
그다음으로는 이 미분방정식이 1계이므로 a0로 나머지 짝수 항들을 정리하여 규칙성을 찾는다.
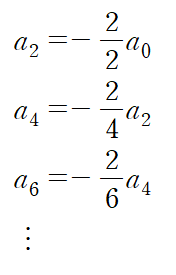
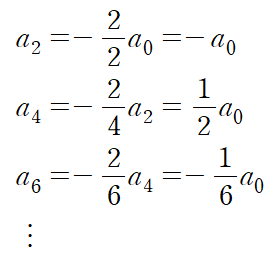
따라서 짝수항들에 대한 표현은 아래와 같고, 이를 적용해 처음에 가정한 해를 정리한다.
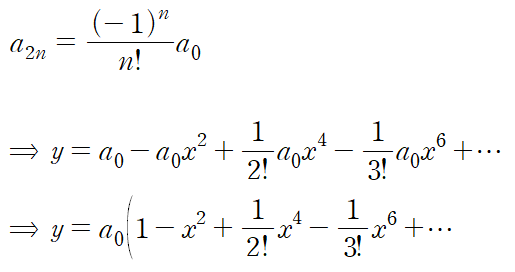
따라서 주어진 미분방정식의 해는 다음과 같다.
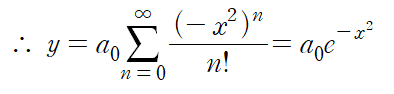
(예제 2) 급수해 방법으로 미분방정식을 풀어라. 이때 5차항까지만 해를 근사하여라
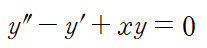
마찬가지로 해를 급수 형태로 가정한다.
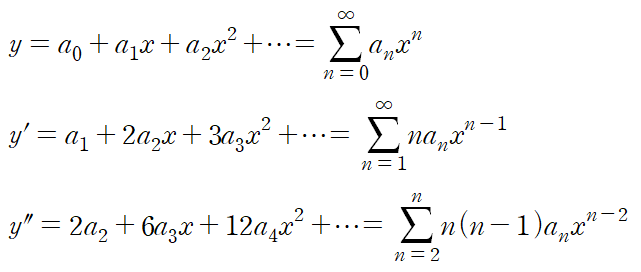
이것을 미분방정식에 대입하고 계수비교를 통해 각 계수들을 정한다.
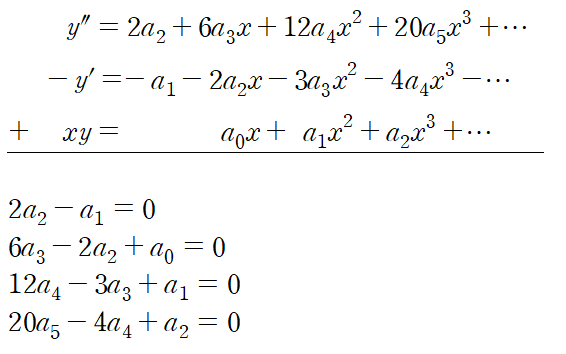
이때 주어진 미분방정식이 2계이므로 일반해를 구성하는 상수는 a0, a1로 잡는다.
a0, a1로 각 항들을 표현하고
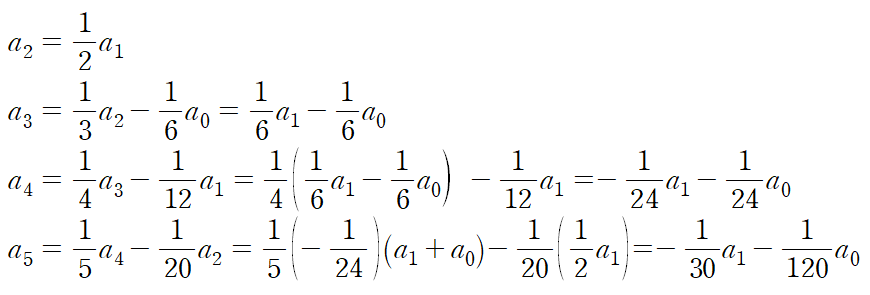
깔끔하게 정리하면 다음과 같다.
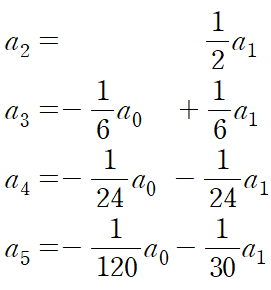
팩토리얼로 표현할 수도 있으며
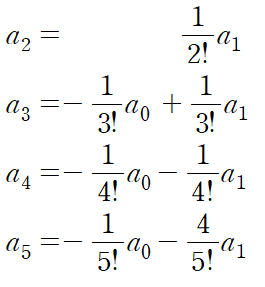
별다른 규칙을 찾을 수 없는 경우에 해당하므로 이런 경우 해를 근사하여 표현한다.
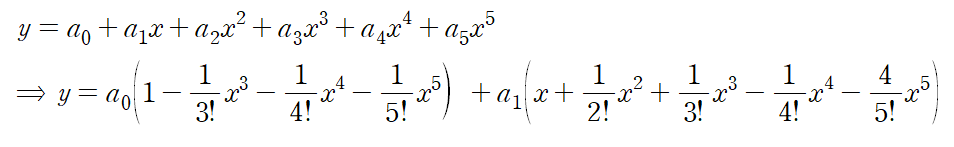
또는 다음과 같이 표현할 수도 있다.
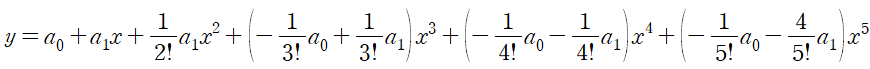
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| 푸리에 급수 예제 (0) | 2024.02.27 |
|---|---|
| [공업수학] dominant eigenvalue와 고유값의 근사, MATLAB code (0) | 2024.01.05 |
| 라플라스 변환 공식 모음 (0) | 2023.04.15 |
| [공업수학] 2.7-1 2계 비제차 미분방정식 : 미정계수법(Method of Undetermined Coefficients) (1) | 2023.01.21 |
| [공업수학] 2.6 론스키 행렬식(Wronskian) (0) | 2023.01.11 |