#선형대수학
#공업수학
Contents
- Eigenvalue(고윳값 또는 고유치) & Eigenvector
- Diagonalization
- Spectral Decomposition
1. Eigenvalue & Eigenvector
고윳값(또는 고유치)과 고유벡터는 정방행렬 A(square matrix, n x n)에 대해 아래 식을 만족하는 상수 λ(lambda, 람다)와 그에 대응되는 영벡터가 아닌 벡터 v를 말한다.

* 고유벡터는 0이 아니어야 하지만 고윳값은 0일 수 있다.
* 각 고유벡터는 앞서 구한 고윳값에 "대응"된다.
위 정의식을 조금 변형하여 고윳값과 고유벡터를 구할 수 있다.

세 번째 줄의 행렬 방정식(벡터 v에 대한 방정식)이 0이 아닌 해를 가져야 한다.
정방행렬 A에 대하여 행렬방정식 Ax = 0이 0이 아닌 해를 가지는 필요충분조건은 행렬 A의 행렬식이 0인 것이다.

이것을 그대로 적용하면 상수 λ에 대한 방정식을 얻는다.

이것을 특성방정식(characteristic equation) 또는 고유방정식이라 부르며 각 행렬마다 가지는 고유한 방정식이다.
일반적으로 A가 nxn 행렬이면 특성방정식은 n차 방정식이 된다.
(예제 1) 행렬 A의 고윳값을 구하여라

특성방정식을 세워 고윳값을 구해주면 된다.

고유벡터는 앞서 구한 고윳값을 사용해 구할 수 있다.

위 방정식의 해가 바로 고윳값 λ에 대한 고유벡터가 된다.
즉 행렬방정식의 해를 직접 구할 수 있어야 고유벡터를 구할 수 있다.
행렬방정식의 해는 "가우스 - 조던 소거법" 또는 Reduced Echelon Form을 통해 구할 수 있다.
https://subprofessor.tistory.com/46
[선형대수학] 선형방정식 (1)
#선형대수학 1. 선형방정식의 형태 (Linear equation) 선형방정식이란 아래와 같이 변수가 모두 일차항으로 이루어진 방정식을 말합니다 나중에 나오겠지만 위와 같은 상수와 변수간의 일차
subprofessor.tistory.com
https://subprofessor.tistory.com/47
[선형대수학] 선형방정식 (2)
#선형대수학 앞선 글) https://subprofessor.tistory.com/46 1. 선형방정식계를 푸는 법 (Solving a linear system) Elementary Row Operations (약어로 ERO, 한글로는 기본 행 연산이라고 번역?) 을 이용해 선형
subprofessor.tistory.com
고유벡터는 infinite solution(무수히 많은 해) 를 가지게 되는데 이중 간단한 것을 취해주면 된다.
(예제 2) 예제 1에서 구한 고윳값들에 대응되는 고유벡터들을 구하여라
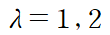
앞서 구한 고윳값을 하나씩 아래 방정식에 넣어 해를 구해주면 된다.
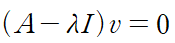
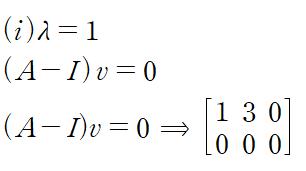
방정식의 해 v가 다음과 같이 x1, x2 두 개의 성분으로 구성된다 할 때

최종적으로 얻은 행렬이 의미하는 것은 다음과 같다.

x1를 자유변수인 x2로 표현하자
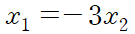
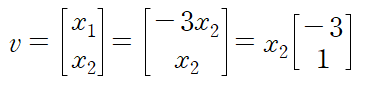
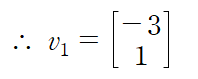
고윳값 2에 대해서도 동일하게 고유벡터를 얻을 수 있다.
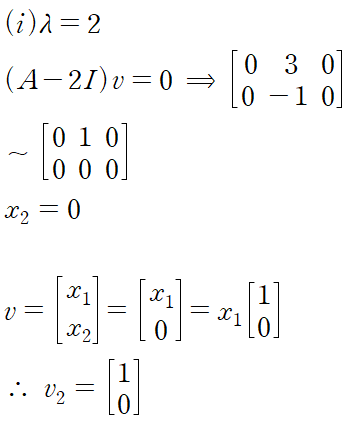
2. Diagonalization
그래서 고윳값과 고유벡터를 어디다가 쓸 수 있는가?
역행렬을 구하는 것에도 쓸 수 있고 행렬의 거듭제곱을 표현하는 것에도 유용하게 사용할 수 있지만
대표적인 응용으로는 대각화가 있다.
대각화란 아래와 같이 행렬 A를 표현할 수 있는 행렬 P와 대각행렬 D를 구하는 것이다.
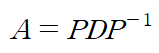
* 행렬 P는 가역행렬(invertible matrix)
* 행렬 D는 대각행렬(diagonal matrix)
이렇게 표현해서 얻을 수 있는 이점은 행렬 A의 거듭제곱을 간단히 표현할 수 있다는 것이다.

대각행렬의 거듭제곱은 각각의 성분의 거듭제곱이기 때문에
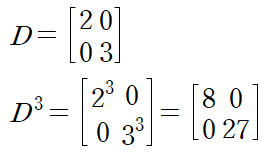
직접 A의 거듭제곱을 계산하는 것보다 훨씬 계산이 용이해진다.
대각화를 하는 규칙은 다음과 같다.
1. 행렬 A의 고윳값과 고유벡터를 구하기
2. 고윳값으로 D 구성
3. 고유벡터들로 P 구성
4. P의 역행렬 구하기
(예제 3) 앞선 예제에서 살펴본 행렬 A에 대해 대각화를 수행하여라
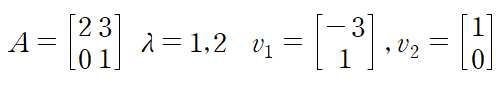
고윳값으로 대각행렬 D를 구성한다.

그 다음으로는 대각행렬에 넣은 고윳값의 순서에 맞춰 고유벡터로 행렬 P를 구성한다.
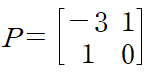
마지막으로 역행렬을 구하면
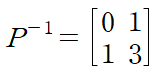
다음과 같이 행렬 A를 대각화할 수 있다.
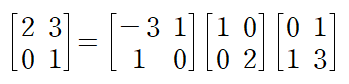
(예제 4) 대각화 : 행렬 B가 중복 고윳값을 가지는 경우
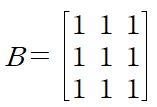
행렬 B의 고윳값을 구하면 0, 0, 3을 얻는다.
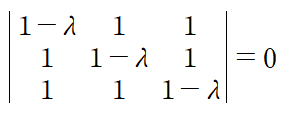
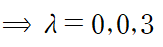
중복되는 고윳값에 대해 중복되는 만큼 고유벡터가 존재할 수도 있고, 그렇지 않을 수도 있다.
이 예제는 고윳값이 중복되는 만큼 고유벡터가 존재하는 경우
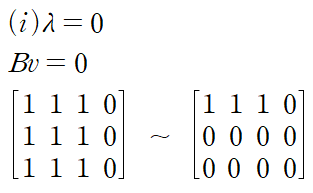
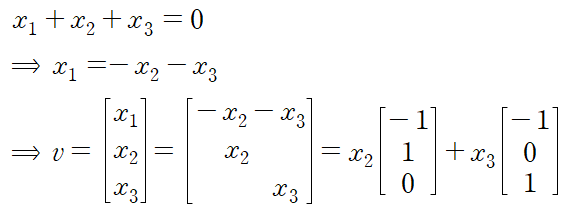
따라서 고윳값 0에 대응되는 고유벡터는 다음과 같다.
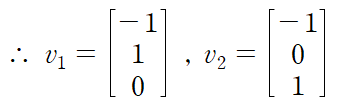
고윳값 3에 대해서도 고유벡터를 구하자
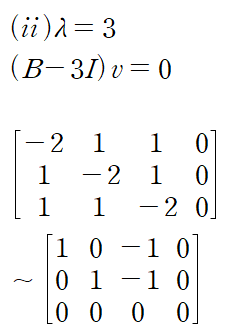

이것으로 대각화에 필요한 D 행렬, P 행렬을 구성하자
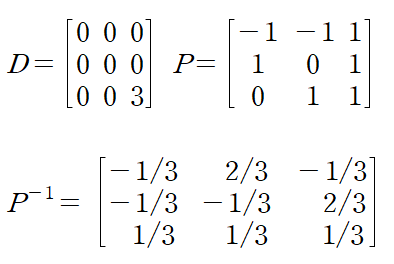
이것으로 대각화가 완료되었다.
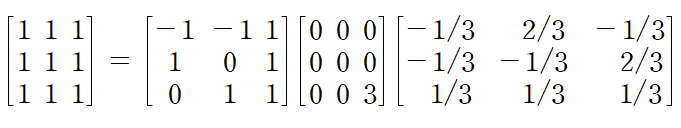
3. Spectral Decomposition
스펙트럼 분해, 스펙트럴 분해로 번역되는데 이것은 특수한 행렬 A에 대한 대각화 방법의 일종이다.
스펙트럼 분해는 행렬 A가 대칭행렬인 경우 사용되는 대각화인데, 그람-슈미트 직교화 과정을 거친다는 특징이 있다.
즉 대칭행렬의 대각화 + 그람-슈미트 -> 스펙트럼 분해 인 것이다.
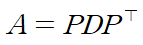
* A는 대칭행렬(symmetric matrix)
* P는 고유벡터로부터 얻은 직교행렬(orthonormal matrix)
대칭행렬이란 대각성분을 기준으로 행렬의 요소들이 대칭되는 행렬을 말하며 다음과 같이 기술된다
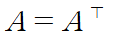
직교행렬 P는 P의 전치행렬과 곱하면 단위행렬을 반환한다
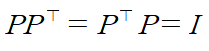
또 직교행렬을 구성하는 행들끼리의 내적, 열들끼리의 내적이 모두 0이라는 특징,
행벡터, 열벡터들의 크기가 모두 1이라는 특징이 있다.
스펙트럼 분해를 수행하는 과정은 다음과 같다.
1. 고윳값과 고유벡터를 구한다. => 고윳값으로 대각행렬 행렬 D를 얻는다.
2. 고유벡터들에 그람-슈미트 과정을 사용해 직교벡터집합을 얻는다
3. 직교벡터들을 각각의 크기로 나눠주어 정교직교벡터집합 P를 얻는다.
4. 대각화 형태로 표현한다.
직교벡터집합은 그람-슈미트 과정을 거쳐 얻은 직교벡터들을 말하고
정규직교벡터집합은 단순히 단위벡터들로 구성된 직교벡터집합을 말한다.
즉 고유벡터 -> 직교벡터 -> 단위(직교)벡터 순서로 P를 구하게 된다.
(예제 5) 앞선 예제 4에서 다룬 B에 대해 스펙트럼 분해를 수행하여라

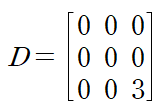
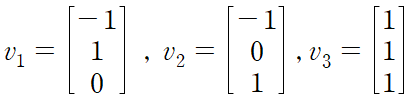
그람-슈미트 과정을 수행하여 직교벡터들을 구하고(v1,v2,v3 => x1, x2, x3)
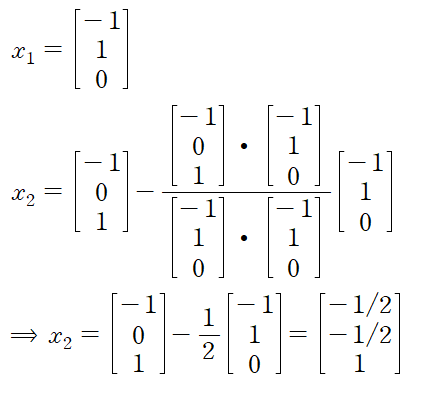
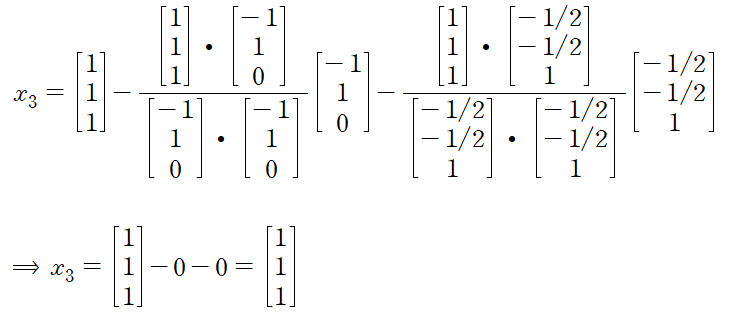
각 벡터를 각각의 크기로 나누어 직교행렬 P를 얻는다
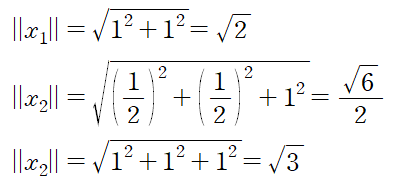
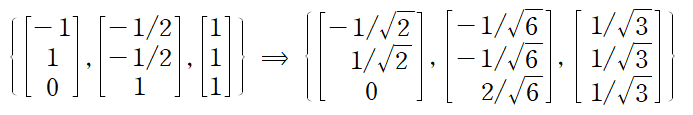
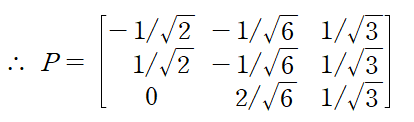
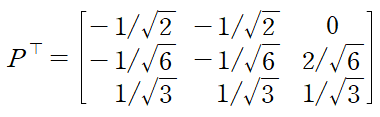
스펙트럼분해의 최종 결과는 다음과 같다.
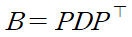
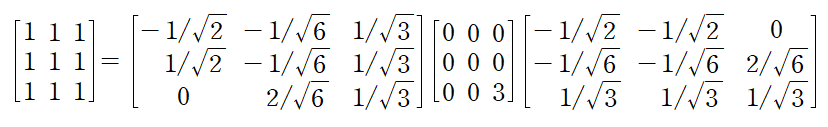
기존의 대각화처럼 행렬의 거듭제곱을 간단히 표현할 수도 있다

스펙트럼 분해의 장점
- 기존 대각화에서는 P의 역행렬을 구해야 하는데 역행렬을 구하는 것보다 단순히 P의 전치행렬을 구하는 것이 용이
- 물론 그람-슈미트 과정이 복잡하게 느껴질 수도 있음
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 선형방정식, 연립방정식 예제 (0) | 2024.04.23 |
|---|---|
| [선형대수학] 회전행렬(Rotation matrix), 회전변환 (0) | 2023.12.28 |
| [선형대수학] 최소제곱법 (Method of Least Squares) (0) | 2022.08.17 |
| [선형대수학] 케일리-해밀턴 정리 : 행렬의 거듭제곱, 역행렬 (Cayley–Hamilton theorem) (0) | 2022.08.15 |
| [선형대수학] 그람-슈미트 과정 (Gram-Schmidt Process) 예제 (0) | 2021.12.21 |