선형방정식에 대해 두 글에 걸쳐서 알아봤는데 이번에는 직접 선형방정식을 풀어보는 시간을 가져봅시다. 예제와 함께 풀이가 나와있긴 하지만 직접 풀고 풀이를 확인하는 것을 추천합니다
(예제 1) 첨가행렬로 표현된 아래 선형방정식계의 해를 구해라
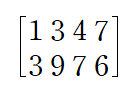
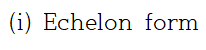
먼저 첨가행렬을 Echelon form으로 바꾸어야 합니다
두 번째 행 중 가장 왼쪽에 위치한 항이 0이 되도록(정확히는 첫 번째 행에 위치한 leading entry 아래가 0이 되도록) 첫 번째 행에 -3을 곱한 것과 두 번째 행을 더하는 ERO(기초 행 연산, Elementary Row Operation)을 수행합시다
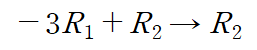
Replacement
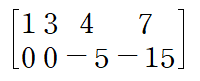
해를 구하기 위해서는 행렬을 Echelon form 다음 Reduced echelon form으로 만들어야 합니다
Reduced echelon form의 조건 두 가지는 다음과 같습니다
일단 두 번째 행의 leading entry를 1로 만들어주겠습니다
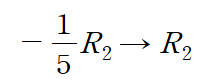
위에서 수행한 ERO는 Scaling입니다
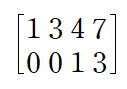
이번에는 두 번째 행의 leading entry 위가 0이 되도록 Replacement를 시행해주겠습니다
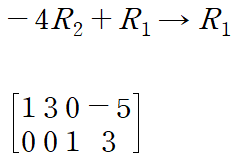
REF.
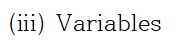
어느정도 풀이가 마무리되어가는 단계입니다
첨가행렬이 네 개의 열(세로줄)을 가지기 때문에 해당 첨가행렬에 대응하는 선형방정식계는 3개의 변수(x1, x2, x3)로 이루어진 방정식입니다(열개수 4에서 상수항 1을 빼 4-1으로 계산)
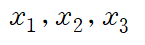
variable
위 변수들이 각각 Basic variable인지 아니면 다른 변수들을 표현해주는 Free variable인지 따져야 합니다
이것은 각 열마다 Leading entry가 존재하느냐로 따질 수 있으며 있는 경우 Basic variable, 없다면 Free variable 입니다
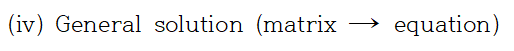
보통 해를 표현할 때 일반해와 특수해를 언급하는데 일반해(General solution)의 경우 구할 수 있는 모든 해를 포함하는 것으로 이해하면 됩니다
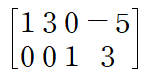
REF로 만들어준 첨가행렬에서 다음과 같은 연립방정식을 얻습니다
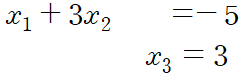
Basic variable에 대하여 정리하면 일반해를 구할 수 있습니다
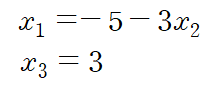
위 해는 x2를 굳이 표현하지 않았습니다(무수히 많은 x2가 가능)
포함하여 표현하면 다음과 같습니다
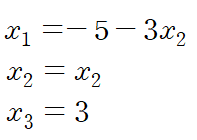
x1, x2, x3를 하나의 열벡터로 모아 표현하면 다음과 같습니다
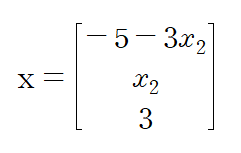
(예제 2) 첨가행렬로 표현된 아래 선형방정식계의 해를 구해라
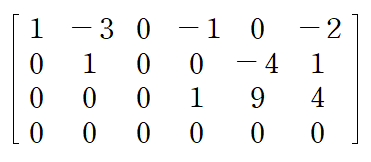
이번 예제의 첨가행렬은 조금 커서 얼핏 겁먹을 수도 있겠습니다만 이미 Echelon form으로 제시되어 있는 데다가 각 행의 Leading entry가 모두 1입니다
두 번째 행의 Leading entry의 위가 -3(0이 아님)이므로 Reduced echelon form은 아니네요 세 번째 행의 Leading entry에서도 REF가 아님을 알 수 있구요
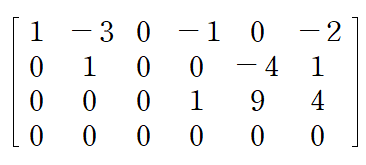
제시된 첨가행렬에 아래와 같은 ERO(Replacement)를 수행하여 두 번째 행 Leading entry 위를 0으로 만들겠습니다
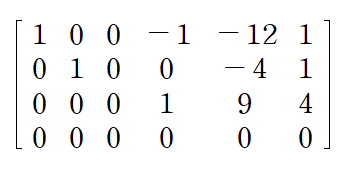
이번에는 세 번째 행 Leading entry 위를 0으로 만들겠습니다
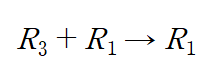
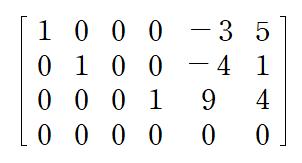
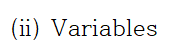
열의 개수가 6개이니까 주어진 선형방정식계(Linear system)의 변수의 개수는 5개입니다
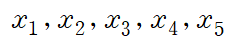
변수들이 Basic 이나 Free 냐는 각 변수와 대응되는 열에 leading entry의 유무로 판단할 수 있습니다
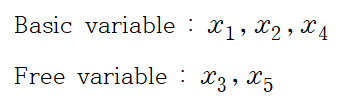
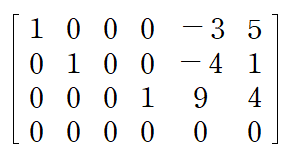
주어진 첨가행렬에서 출발한 REF를 다시 연립방정식 형태로 바꿉니다
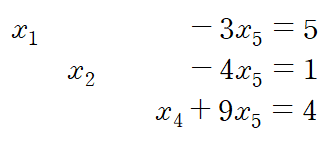
이를 Basic variable에 대해 정리하면 일반해(General solution)를 얻습니다
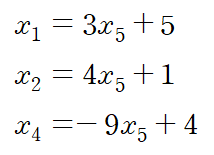
☕ 커피 한 잔보다 싼 선형대수학 모의고사 ☕
잘 공부하고 있는지 확인하실 수 있도록
기말고사를 대비할 수 있는 가벼운 모의고사를 준비했습니다.
✅ 커피 한 잔보다 싼 3,900원
✅ 총 12문제, 상세한 해설 포함 (20p가량)
✅ 문제와 해설 모두 한국어입니다.
✅ 출제단원
- 연립방정식
- LU분해
- 그람-슈미트 과정
- QR분해
- 고유값과 고유벡터
- 역행렬
- 특잇값 분해(SVD)
🚫 본 모의고사는 시험 대비 및 복습용으로 제작되었습니다.
🚫 자료의 무단 배포 및 판매 시 저작권법에 의한 처벌을 받을수 있습니다
🚫 전자책 특성 상 환불이 불가합니다.
✉️ 질문 및 기타 문의는 hyonklee@gmail.com
시험지 샘플입니다.
해설 샘플입니다.
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| 특이값 분해(Singular Value Decomposition; SVD) 예제 (0) | 2024.05.23 |
|---|---|
| [선형대수학] 회전행렬(Rotation matrix), 회전변환 (0) | 2023.12.28 |
| [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지 (1) | 2023.12.12 |
| [선형대수학] 최소제곱법 (Method of Least Squares) (0) | 2022.08.17 |
| [선형대수학] 케일리-해밀턴 정리 : 행렬의 거듭제곱, 역행렬 (Cayley–Hamilton theorem) (0) | 2022.08.15 |