#선형대수학
고윳값과 고유벡터에 대한 내용은 아래 글 참조 바랍니다
[선형대수학] 고윳값, 고유벡터, 고유공간 (Eigenvalue, Eigenvector, Eigenspace)
#선형대수학 1. 고윳값과 고유벡터의 정의 n x n 행렬 A에 대해 위 등식을 만족하는 λ(lambda)와 x를 각각 고윳값(Eigenvector), 고유벡터(Eigenvector)라 합니다 위와 같은 2 x 2 행렬을 생각해봅.
subprofessor.tistory.com
https://subprofessor.tistory.com/57
[선형대수학] 특성방정식, 고윳값과 고유벡터 구하기
#선형대수학 1. 특성방정식 (Characteristic Equation) 특성다항식(Characteristic Polynomial)이라고도 하는데, 행렬의 고윳값을 구하기 위한 도구입니다 위 식을 특성방정식이라 부르는데, 유
subprofessor.tistory.com
1. 케일리-해밀턴 정리(Cayley–Hamilton theorem)

케일리-해밀턴 정리는 고윳값이 포함된 방정식인 특성방정식에 고윳값 대신에 행렬 A를 넣어도 성립한다는 정리입니다.

위 식이 n x n 행렬 A의 특성방정식이라 할 때 다음 관계식이 성립합니다.

☆ 식 (1)은 scarlar 에 대한 방정식이고 식 (2)는 matrix에 대한 방정식입니다.
2. 행렬의 거듭제곱 (Power of matrices)
행렬의 거듭제곱은 대각화를 통해서도 쉽게 구할 수 있지만 특성방정식과 케일리-해밀턴 정리를 이용해 구할 수도 있습니다.
2 x 2 행렬 A의 특성방정식을 봅시다.



위 식에 λ 대신 A를 대입하고 (ad-bc) 옆에 단위행렬(Identity matrix)을 곱해주면 다음 식을 얻습니다.

A의 제곱항만 좌변에 남겨두면 A와 I만을 이용해 A의 제곱을 표현할 수 있습니다.

(예제 1) 주어진 행렬에 대해

을 구하여라

먼저 특성방정식을 구합니다.
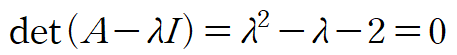
λ 대신 A를 대입해 A의 제곱을 구할 수 있습니다.
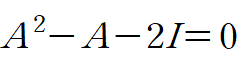
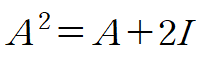
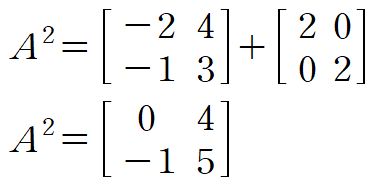
A의 세제곱의 경우 식 (3)의 양변에 행렬 A를 곱해서 구할 수 있습니다.
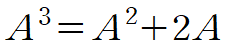
위 식에 앞서 구한 식 (3)를 대입해 간단히 정리합니다.
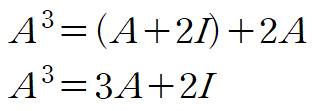
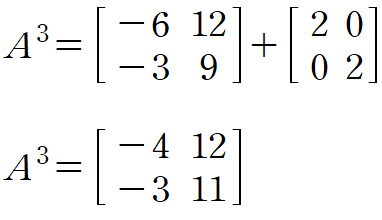
앞선 예제에서는 A의 세제곱까지 구해보았는데 같은 방식을 사용한다면 거듭제곱이 커지더라도 행렬 A의 거듭제곱은 A와 I의 선형결합으로 표현이 된다는 것을 볼 수 있습니다.
임의의 음이 아닌 정수 m에 대해 다음과 같이 행렬 A의 거듭제곱이 표현된다고 합시다.
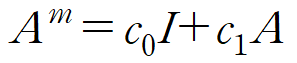
식 (4)에 케일리-해밀턴 정리를 역으로 적용하면 λ 의 관계식을 얻습니다.
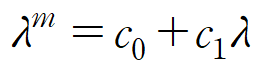
앞서 구한 특성방정식의 해를 식 (5) 에 대입해 c1과 c0를 얻습니다.
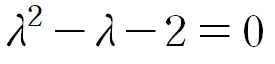
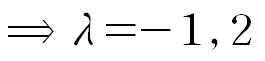

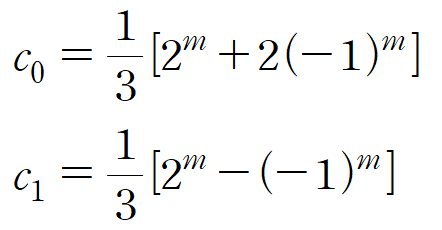
이를 다시 식 (4) 에 대입하여 행렬 A의 거듭제곱을 구할 수 있습니다.
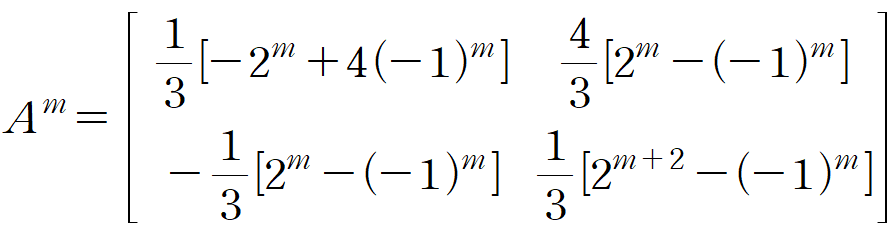
3. 역행렬 (Inverse of matrices)
만약 n x n 행렬 A가 역행렬을 가진다면(가역행렬, Invertible matrix), 케일리-해밀턴 정리를 이용해 특성방정식으로 역행렬을 구할 수 있습니다.
앞선 예제에서 보았던 행렬을 살펴봅시다.
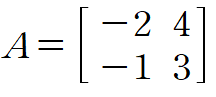
케일리-해밀턴 정리를 적용한 식을 단위행렬(Identity matrix)에 대해 정리합니다.
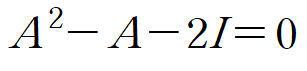
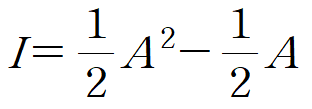
이때 행렬 A는 det A = -2 이므로 역행렬을 가집니다.
이 역행렬을 식 (6) 의 양변에 곱합니다.
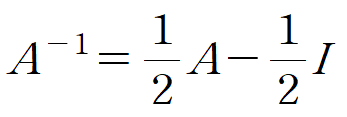
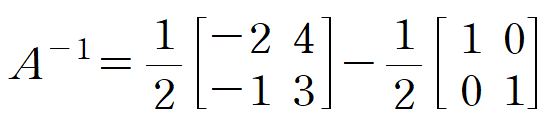
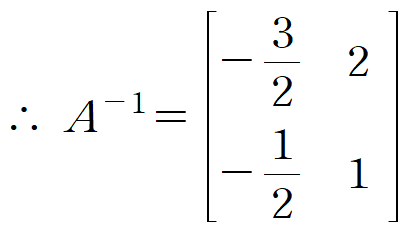
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 고윳값, 고유벡터부터 대각화, 스펙트럼 분해까지 (1) | 2023.12.12 |
|---|---|
| [선형대수학] 최소제곱법 (Method of Least Squares) (0) | 2022.08.17 |
| [선형대수학] 그람-슈미트 과정 (Gram-Schmidt Process) 예제 (0) | 2021.12.21 |
| [선형대수학] 크래머 공식 (Cramer's Rule) (0) | 2021.11.18 |
| [선형대수학] 특성방정식, 고윳값과 고유벡터 구하기 (0) | 2021.11.12 |