#선형대수학
1. 선형방정식의 형태 (Linear equation)
선형방정식이란 아래와 같이 변수가 모두 일차항으로 이루어진 방정식을 말합니다

나중에 나오겠지만 위와 같은 상수와 변수간의 일차항 합 꼴의 형태를 '선형결합'(linear combination)이라고 합니다
변수들은 모두 개별항으로 존재하여야 하며, 아래 세 가지 경우는 모두선형방정식이 아닌 예시들입니다.

(예제 1) 다음 중 선형방정식이 아닌 것을 골라라

답은 2번입니다
2. 선형방정식계 (Systems of linear equation)
선형방정식이 1개 또는 그 이상이 모인 것을 '계'라 합니다(system, 시스템)
(교재 원문 : A system of linear equations (or a linear system) is a collection of one or more linear equations involving the same variables)
System of linear equation 이라 하고 간단히 linear system 이라고 부르기도 합니다

고등학교 때 배웠던 연립방정식과 비슷한 느낌입니다
이 선형방정식계의 해(solution)는 (s1, s2, . . . )와 같은 집합의 형태로 표현할수 있습니다
만약 어떤 두 선형방정식계가 같은 해 집합(solution set)을 가지고 있다면 두 선형방정식은 상등(equivalent)이라 합니다
(교재 원문 : Two linear systems are called equivalent if they have the same solution set)
3. 선형방정식의 해 (Solutions of linear equations)
선형방정식계의 해는 다음 세 가지 형태 중 하나입니다

해가 존재하지 않을 때 선형방정식계가 inconsistent / 존재하는 경우 consistent라고 분류됩니다
4. 선형방정식의 행렬표기법 (Matrix notation)
아래와 같은 선형방정식계를 생각해봅시다

변수가 2, 3개일 때는 괜찮은데 점점 늘어나면 반복해서 사용되는 변수(x1, x2, . . . )들을 사용하기가 너무 귀찮으니까 다음과 같이 선형방정식계의 계수만을 딴 '계수행렬'(coefficient)을 이용해 표현합니다
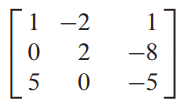
이때 계수행렬은 좌변의 변수들의 계수만을 표시합니다. 통상적으로 우변에 0을 비롯한 상수항이 위치하게 되는데 이것은 행렬에 포함하지 않는데 상수항까지 나타낸 행렬표기를 '첨가행렬'(augmented matrix)이라고 합니다.
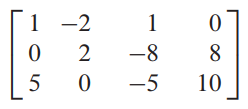
첨가행렬이 초반에는 조금씩 등장하는데 나중가면 우변이 0인 경우들을 주로 다루기 때문에 ( n x n 행렬의 특성을 살리기 위해 ) 그냥 이런 게 있구나 정도로 알고 넘어가시면 됩니다
행렬의 크기(size of matrix)는 몇 개의 행과 열로 이루어져있냐로 따지느데, m개의 행(row)과 n개의 열(column)로 이루어진 행렬을 m x n 행렬이라 합니다 (m by n matrix)
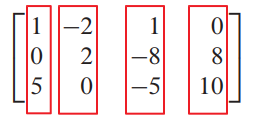
위에 예시로 든 두 행렬은 각각 3x3, 3x4 행렬입니다 (행렬이라는 이름을 따라서 행의 개수가 앞에 온다고 기억하면 편합니다)
이 선형방정식계를 푸는 구체적인 방법은 다음 글에서 알아봅시다

☕ 커피 한 잔보다 싼 선형대수학 모의고사 ☕
✅ 선형대수학 연립 일차 방정식 단원 모의고사 2회분입니다.
✅ 문제는 영어, 해설은 한국어입니다.
✅ 회당 10문제, 상세한 해설 포함 (12p가량)
🚫 본 모의고사는 시험 대비 및 복습용으로 제작되었습니다.
🚫 모든 문제의 저작권은 섭교수 연구소에 있으며 자료의 무단 배포 및 판매를 금지합니다.
🚫 전자책 특성 상 환불이 불가합니다.
✉️ 질문 및 기타 문의는 hyonklee@gmail.com
시험지 샘플입니다.


해설 샘플입니다.

Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 열공간과 영공간 (Column Space and Null Space) (7) | 2021.11.01 |
|---|---|
| [선형대수학] 부분공간, 기저 (Subspace, Basis) (0) | 2021.10.30 |
| [선형대수학] 차원, 랭크 (Dimension, Rank) (0) | 2021.10.29 |
| [선형대수학] 열공간과 영공간 (0) | 2021.10.27 |
| [선형대수학] 선형방정식 (2) (0) | 2021.10.19 |